字符串总结-三大“自动机”
复习笔记-字符串算法
AC自动机
本质
在字典树上进行KMP匹配
实现思路
正常建立Trie树
处理失配指针
在AC自动机中,失配指针fail和KMP的next是一样的作用,如下图(from SuperJvRuo)
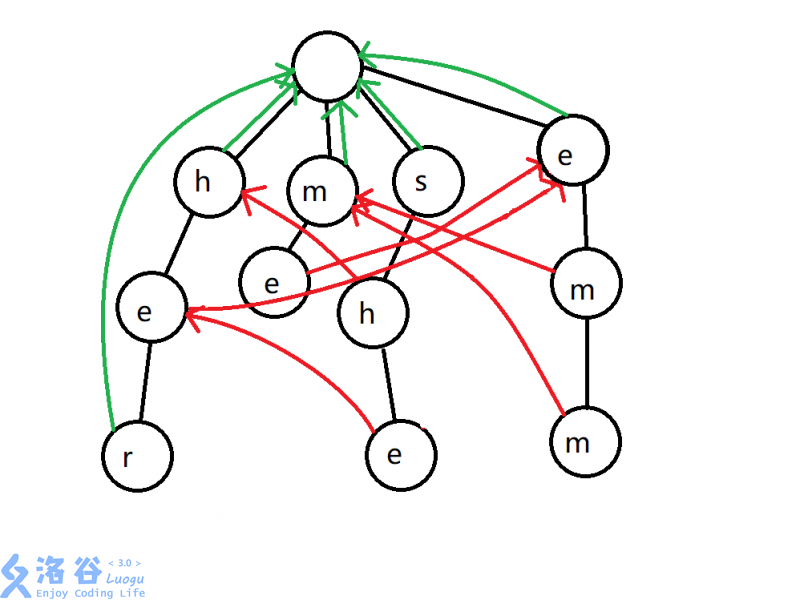
不难看出fail指针的构造方法:通过Bfs,设这个节点上的字母为c,沿着他父亲的fail走,直到走到一个节点,他的儿子中也有字母为c的节点,我们就找到了所求的fail。
匹配
类比KMP,我们可以先在树上走,如果失去匹配,就跳fail指针
优化
进行路径压缩,把Trie树变成图
代码实现

#include <bits/stdc++.h>
const int maxn = 1000010;
char ss[maxn];
struct node {
node *ch[26];
int exist;
node *fail;
node(): exist(0), fail(0) {
memset(ch, 0, sizeof ch);
}
};
node *root = new node;
void insert(char *s) {//字典树建立
node *p = root;
for (int i = 0; s[i]; ++i) {
int x = s[i] - 'a';
if (p -> ch[x] == NULL) p -> ch[x] = new node;
p = p -> ch[x];
}
++p -> exist;
}
void get_fail() {//处理失配指针
node *p, *tmp;
std::queue<node*> q;
q.push(root);
while (!q.empty()) {
tmp = q.front();
q.pop();
for (int i = 0; i < 26; ++i)
if (tmp -> ch[i]) {
if (tmp == root) {
tmp -> ch[i] -> fail = root;
} else {
p = tmp -> fail;
while (p) {
if (p -> ch[i]) {
tmp -> ch[i] -> fail = p -> ch[i];
break;
}
p = p -> fail;
}
if (p == NULL) tmp -> ch[i] -> fail = root;
}
q.push(tmp -> ch[i]);
}
}
}
int AC(char *s) {//匹配
int cnt = 0;
int l = strlen(s);
node *p = root;
for (int i = 0; i < l; ++i) {
int x = s[i] - 'a';
while (!p -> ch[x] and p != root) p = p -> fail;
p = p -> ch[x];
if (!p) p = root;
node *tmp = p;
while (tmp != root) {
if (tmp -> exist >= 0) cnt += tmp -> exist, tmp -> exist = -1;
else break;
tmp = tmp -> fail;
}
}
return cnt;
}
int main() {
int n;
scanf("%d", &n);
while (n--) {
scanf("%s", ss);
insert(ss);
}
get_fail();
scanf("%s", ss);
printf("%d", AC(ss));
return 0;
}
回文自动机
不是很熟
本质
是两棵回文树。其中一个维护长度为奇数的字符串,另一个是长度为偶数的字符串
结构
- 回文自动机的每一条边代表一个字符。对于每一条边,它的起点字符串左右都加上这个字符就得到终点的字符串
- 回文自动机的每一个节点代表一个字符串,它的每一个子节点都是它在左右两端分别加上相同的字符得到的
- 回文自动机的每一个节点都有一个fail指针,它指向这个字符串最长满足回文的后缀的节点。如果没有,就指向根。
建树
直接在字符串两端进行扩展。每次要加入一个点的时候,先跳最后加入的一个节点的fail指针,直到满足节点字符等于新加入字符。然后加入新节点,把刚刚找到的那个节点的对应边连到新节点上, 更新节点维护的所有值
代码实现

1 #include<cstdio>
2
3 const int maxn=555555;
4
5 int cnt=1;
6 char s[maxn];
7 int son[maxn][26];
8 int len[maxn],fail[maxn];
9
10 int new_node(int length)
11 {
12 len[++cnt]=length;
13 return cnt;
14 }
15
16 int get_fail(char T[],int pre,int now)
17 {
18 while(T[now-len[pre]-1]!=T[now])
19 pre=fail[pre];
20 return pre;
21 }
22
23 void build(char T[])
24 {
25 int last=0;
26 len[0]=0,len[1]=-1;
27 fail[0]=1,fail[1]=1;
28 for(int i=1;T[i];i++)
29 {
30 int cur=get_fail(T,last,i);
31 if(!son[cur][T[i]-'a'])
32 {
33 int now=new_node(len[cur]+2);
34 fail[now]=son[get_fail(T,fail[cur],i)][T[i]-'a'];
35 son[cur][T[i]-'a']=now;
36 }
37 last=son[cur][T[i]-'a'];
38 }
39 }
40
41 int main()
42 {
43 scanf("%s",s+1);
44 build(s);
45 printf("%d\n",cnt-1);
46 return 0;
47 }
后缀自动机
不是很熟+1
结构
一个DAG,满足从根出发走到所有结束点的所有路径都是字符串的一个后缀
构造过程
每次尽可能利用上一次的状态得到新的状态。我也说不明白,背的板子。。
用途
可以解决哈希解决不了的所有字符串问题。广义后缀自动机还可以解决其他很多问题。
代码实现

1 #include<cstdio>
2 #include<cstring>
3 #include<algorithm>
4
5 typedef long long ll;
6 const int maxn=1111111;
7
8 struct node
9 {
10 int son[26];
11 int len,link;
12 }sam[maxn<<1];
13
14 int cnt=1,last=1;
15 int size[maxn<<1];
16
17 void insert(int ch)
18 {
19 int cur=++cnt;
20 sam[cur].len=sam[last].len+1;
21 int p=last;
22 while(p&&!sam[p].son[ch])
23 {
24 sam[p].son[ch]=cur;
25 p=sam[p].link;
26 }
27 if(!p) sam[cur].link=1;
28 else
29 {
30 int q=sam[p].son[ch];
31 if(sam[p].len+1==sam[q].len) sam[cur].link=q;
32 else
33 {
34 int clone=++cnt;
35 sam[clone].len=sam[p].len+1;
36 sam[clone].link=sam[q].link;
37 memcpy(sam[clone].son,sam[q].son,sizeof(sam[q].son));
38 while(p&&sam[p].son[ch]==q)
39 {
40 sam[p].son[ch]=clone;
41 p=sam[p].link;
42 }
43 sam[q].link=sam[cur].link=clone;
44 }
45 }
46 size[cur]=1;
47 last=cur;
48 }
49
50 ll ans;
51 char s[maxn];
52 int tong[maxn];
53 int topo[maxn<<1];
54
55 int main()
56 {
57 scanf("%s",s+1);
58 int len=strlen(s+1);
59 for(int i=1;i<=len;i++)
60 insert(s[i]-'a');
61 for(int i=1;i<=cnt;i++)
62 tong[sam[i].len]++;
63 for(int i=1;i<=len;i++)
64 tong[i]+=tong[i-1];
65 for(int i=cnt;i>=1;i--)
66 topo[tong[sam[i].len]--]=i;
67 for(int i=cnt;i>=1;i--)
68 {
69 int now=topo[i];
70 size[sam[now].link]+=size[now];
71 if(size[now]>1)
72 ans=std::max(ans,1LL*size[now]*sam[now].len);
73 }
74 printf("%lld\n",ans);
75 return 0;
76 }




