数据结构-FHQ Treap（也许是全网唯一一个认真给你画图解的）

平衡树-FHQTreap

FHQTreap，又称非旋转Treap，顾名思义，是FHQ发明的不用旋转来维护随机key值的小根堆性质的平衡树。

树的结点

为了方便树的各种操作，本蒟蒻的FHQ每个节点只存一个数而不是相等的所有数，保证LC<now<=RC，代码是这样的

 1 struct Node{
 2     Node *child[2];
 3     int val, key, size;
 4 
 5     Node(int val):val(val), size(1), key(Rand()) {
 6         child[0] = child[1] = NULL;
 7     }
 8 
 9     void Update() {
10         size = 1;
11         if (child[0]) size += child[0]->size;
12         if (child[1]) size += child[1]->size;
13     }
14 }

其中key是随机值

基本操作（一）——分裂Split

功能

Split可以把以now为根的子树分成两个部分，tree1为前k小的值，tree2为剩余部分，返回两颗新树的树根

拆解步骤

边界：
(1) 如果now为空树，两新树都为空树
(2) 如果k为0，tree1为空，tree2为原树
(3) 如果k>=原树的节点数，tree1为原树，tree2为空
记录原树左子树的size
如果k <= lsize，递归拆左子树，否则递归拆右子树
按需要拼回两个子树，return

是不是没听懂3、4步？行，还有图解。

情况一

假设k <= lc，我们需要递归拆左子树，我们来画一张图

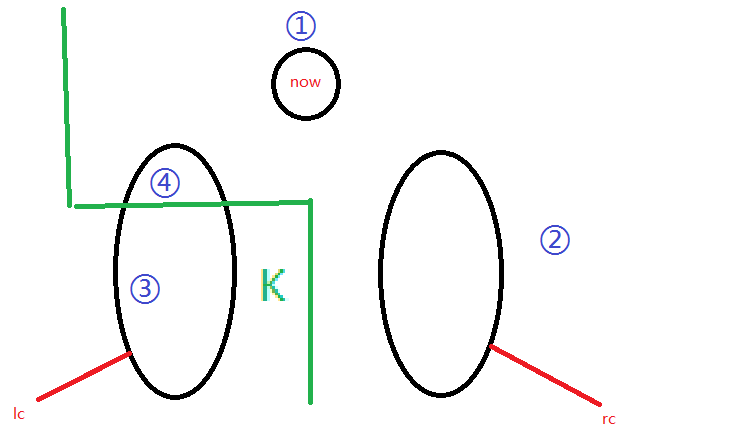
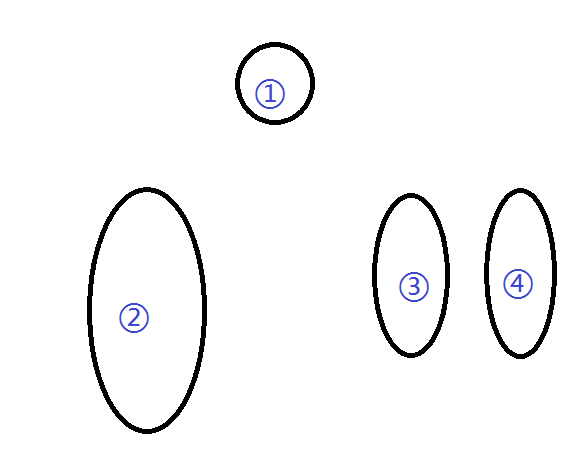
如上图，我们分为四部分看：①原根，②右子树，③左子树k内部分，④左子树k外部分

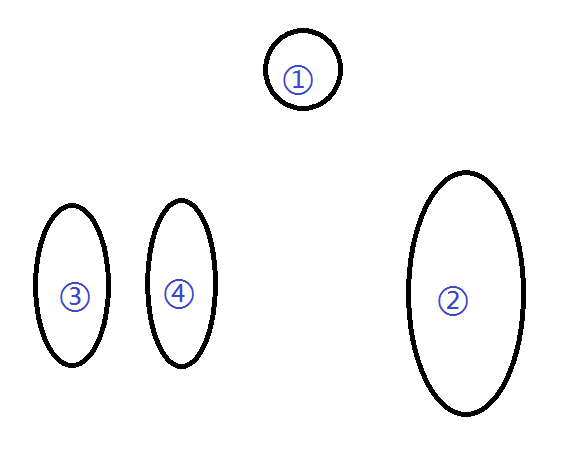
我们对左子树调用split，把③④分开

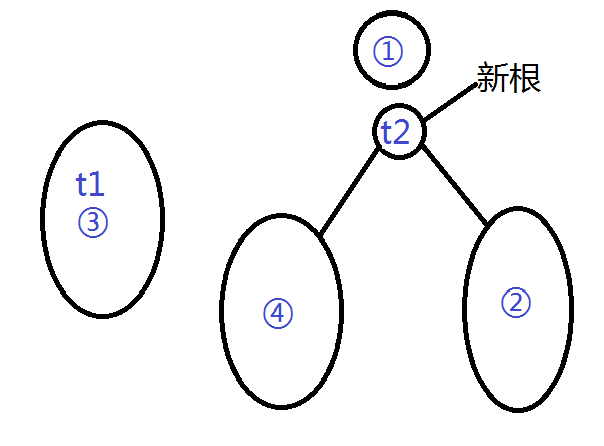
最后，我们把原根①的信息复制到一个new结点里，delete掉①

新结点左面挂递归掰出来的④，右面挂②也就是原来的右子树，这样形成了t2

递归出来的③也就成为了t1

情况二，与前一种相反

k > ls，此时我们仍然来把它分成四部分

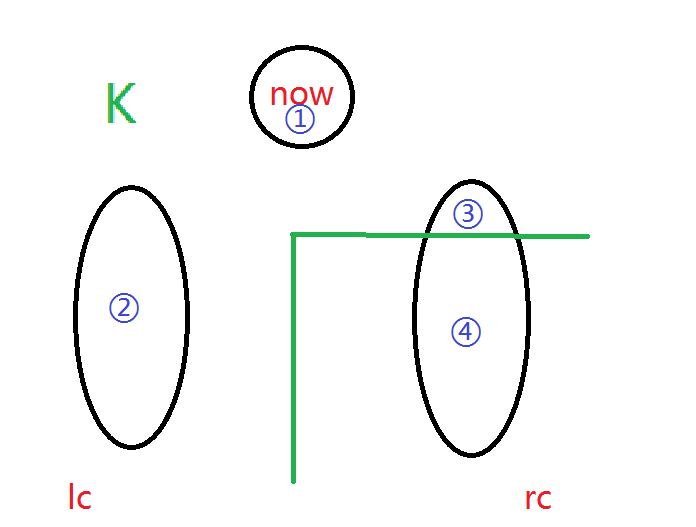
k包括①②③三部分，④为右子树的剩余部分。不难看出，③的size是k - ls - 1（划重点）。

知道了③的size，那么我们也可以对右子树使用split，把③和④掰开。

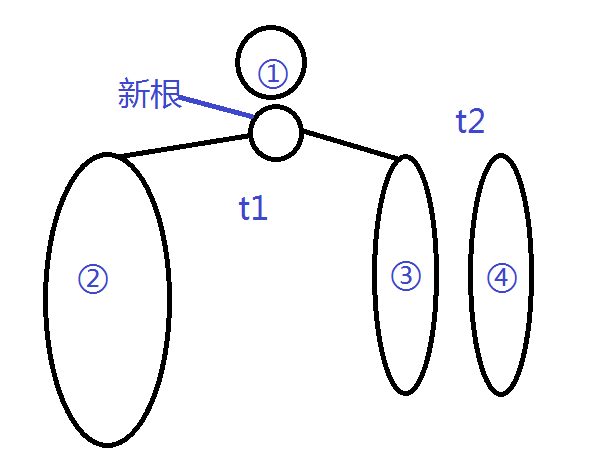
然后就跟刚才一样了，复制①挂②③作为t1，④作为t2

接下来是喜闻乐见的代码

如果使用STL的pair来返回两个根，那么就可以特别快乐的这样搞定

 1 pair<Node*, Node*> Split(Node* now, int k) {
 2     Node* null = NULL;
 3     if (!now) return make_pair(null, null);
 4     if (!k) return make_pair(null, now);
 5     if (k >= now->size) return make_pair(now, null);
 6 //------以上为判定边界--------
 7     int ls = now->child[0] ? now->child[0]->size : 0;//记录ls
 8     if (ls >= k) {//情况二
 9         pair<Node*, Node*> temp = Split(now->child[0], k);//拆左子树
10         Node* b = new Node(now->val);//建新根，挂新子树
11         b->key = now->key;
12         b->child[0] = temp.second;
13         b->child[1] = now->child[1];
14         b->Update();
15         delete now;
16         return make_pair(temp.first, b);
17     } else {//情况一
18         pair<Node*, Node*> temp = Split(now->child[1], k - ls - 1);
19         Node* a = new Node(now->val);//建新根，挂新子树
20         a->key = now->key;
21         a->child[1] = temp.first;
22         a->child[0] = now->child[0];
23         a->Update();
24         delete now;    
25         return make_pair(a, temp.second);
26     }
27 }

重点：NULL不能直接存在pair里，需要新建一个null指针代替NULL

如果不想使用pair或者是建一个null，也可以在调用前临时建两个指针来存拆出来的两个子树，然后在函数中传址调用来让它们指向两棵新树，代码如下

 1 void Split(Node *now, int k, Node *&t1, Node *&t2) {
 2     if (!now) {
 3         t1 = t2 = NULL; return;
 4     } 
 5     if (!k) {
 6         t1 = NULL; t2 = now; return;
 7     }
 8     if (k >= now->size) {
 9         t1 = now; t2 = NULL; return;
10     }
11     int ls = now->child[0] ? now->child[0]->size : 0;
12     if (ls >= k) {
13         Node *temp;
14         Split(now->child[0], k, t1, temp);
15         t2 = now; t2->child[0] = temp; 
16         t2->Update(); return;
17     } else {
18         Node *temp;
19         Split(now->child[1], k - ls - 1, temp, t2);
20         t1 = now; t1->child[1] = temp;
21         t1->Update(); return;
22     }
23 }

这样也很清晰明了

情况（二）——合并Merge

这个函数就比较简单了，把a, b两棵树捏到一起，返回新根。流程如下

判断边界：如果a空返回b，如果b空返回a
如果akey < bkey，调用Merge，把b和a的右子树捏到一起作为a的右子树
如果akey >= bkey，调用Merge，把a和b的左子树捏到一起作为b的左子树

应该还好理解，放代码

 1 Node* Merge(Node* a, Node* b) {
 2     if (!a) return b;
 3     if (!b) return a;//判断边界
 4     if (a->key < b->key) {
 5         a->child[1] = Merge(a->child[1], b);//递归调用
 6         a->Update();//记得更新
 7         return a;//返回新根
 8     } else {
 9         b->child[0] = Merge(a, b->child[0]);//递归调用
10         b->Update();//记得更新
11         return b;//返回新根
12     }
13 }

注意：调用时保证b根的值>=a根的值

其他操作：查Rank，前驱，后继

就是普通的二叉搜索树操作，直接放代码了

 1 int Rank(Node* now, int k) {
 2     if (!now) return 0;
 3     int ls = now->child[0] ? now->child[0]->size : 0;
 4     if (now->val <= k)
 5         return ls + 1 + Rank(now->child[1], k);
 6     else
 7         return Rank(now->child[0], k);
 8 }
 9 
10 int GetPre(Node *now, int k) {
11     int ans = -INF;
12     while (now) {
13         if (now->val < k) {
14             ans = max(ans, now->val);
15             now = now->child[1];
16         } else {
17             now = now->child[0];
18         }
19     }
20     return ans;
21 }
22 
23 int GetSuc(Node *now, int k) {
24     int ans = INF;
25     while (now) {
26         if (now->val > k) {
27             ans = min(ans ,now->val);
28             now = now->child[0];
29         } else {
30             now = now->child[1];
31         }
32     }
33     return ans;
34 }

基于Split和Merge的操作：插入、删除、查找第k小

插入：查一下新数的rank，然后拆成 <rank 和 >=rank 两部分，然后把新结点与它们合并

pair版

1 void Insert(int val) {
2     int rank = Rank(root, val);
3     pair<Node*, Node*> temp = Split(root, rank);
4     Node* nod = new Node(val);
5     root = Merge(temp.first, nod);
6     root = Merge(root, temp.second);
7 }

普通版

1 void Insert(int val) {
2     int rank = Rank(root, val);
3     Node *temp1, *temp2;
4     Split(root, rank, temp1, temp2);
5     Node *nod = new Node(val);
6     root = Merge(temp1, nod);
7     root = Merge(root, temp2);
8 }

删除：查rank，拆出rank个，t1中拆出rank - 1个，把中间那个删掉，剩下的拼回去

pair版

1 void Remove(int val) {
2     int rank = Rank(root, val);
3     pair<Node*, Node*> t1 = Split(root, rank), t2 = Split(t1.first, rank - 1);
4     root = Merge(t2.first, t1.second); delete t2.second;
5 }

普通版

1 void Remove(int val) {
2     int rank = Rank(root, val);
3     Node *t11, *t12, *t21, *t22;
4     Split(root, rank, t11, t12);
5     Split(t11, rank - 1, t21, t22);
6     root = Merge(t21, t12);
7     delete t22;
8 }

查第k小：拆出k - 1个，t2中拆出1个，返回中间那个结点的值，最后拼回去

pair版

1 int FindKth(int k) {
2     pair<Node*, Node*> x = Split(root, k - 1);
3     pair<Node*, Node*> y = Split(x.second, 1);
4     Node* now = y.first;
5     root = Merge(x.first, Merge(now, y.second));
6     return now ? now->val : 0;
7 }

普通版

1 int FindKth(int k) {
2     Node *x1, *x2, *y1, *y2;
3     Split(root, k - 1, x1, x2);
4     Split(x2, 1, y1, y2);
5     Node *now = y1;
6     root = Merge(x1, Merge(now, y2));
7     return now ? now->val : 0;
8 }

最后，模板题完整代码

pair版

#include <cstdio>
#include <algorithm>

using std::pair;
using std::make_pair;
using std::min;
using std::max;

const int INF = 2147483647;

struct Node{
    Node* child[2];
    int val, key, size;

    Node(int val):val(val), size(1), key(rand()) {
        child[0] = NULL; child[1] = NULL;
    }

    void Update() {
        size = 1;
        if (child[0]) size += child[0]->size;
        if (child[1]) size += child[1]->size;
    }
};

Node *root;

Node* Merge(Node* a, Node* b) {
    if (!a) return b;
    if (!b) return a;
    if (a->key < b->key) {
        a->child[1] = Merge(a->child[1], b);
        a->Update();
        return a;
    } else {
        b->child[0] = Merge(a, b->child[0]);
        b->Update();
        return b;
    }
}

pair<Node*, Node*> Split(Node* now, int k) {
    Node* null = NULL;
    if (!now) return make_pair(null, null);
    if (!k) return make_pair(null, now);
    if (k >= now->size) return make_pair(now, null);
    int ls = now->child[0] ? now->child[0]->size : 0;
    if (ls >= k) {
        pair<Node*, Node*> temp = Split(now->child[0], k);
        Node* b = new Node(now->val);
        b->key = now->key;
        b->child[0] = temp.second;
        b->child[1] = now->child[1];
        b->Update();
        delete now;
        return make_pair(temp.first, b);
    } else {
        pair<Node*, Node*> temp = Split(now->child[1], k - ls - 1);
        Node* a = new Node(now->val);
        a->key = now->key;
        a->child[1] = temp.first;
        a->child[0] = now->child[0];
        a->Update();
        delete now;
        return make_pair(a, temp.second);
    }
}

int Rank(Node* now, int k) {
    if (!now) return 0;
    int ls = now->child[0] ? now->child[0]->size : 0;
    if (now->val <= k)
        return ls + 1 + Rank(now->child[1], k);
    else
        return Rank(now->child[0], k);
}

int GetPre(Node* now, int k) {
    int ans = -INF;
    while (now) {
        if (now->val < k) {
            ans = max(ans, now->val);
            now = now->child[1];
        } else {
            now = now->child[0];
        }
    }
    return ans;
}

int GetSuc(Node* now, int k) {
    int ans = INF;
    while (now) {
        if (now->val > k) {
            ans = min(ans, now->val);
            now = now->child[0];
        } else {
            now = now->child[1];
        }
    }
    return ans;
}

int FindKth(int k) {
    pair<Node*, Node*> x = Split(root, k - 1);
    pair<Node*, Node*> y = Split(x.second, 1);
    Node* now = y.first;
    root = Merge(x.first, Merge(now, y.second));
    return now ? now->val : 0;
}

void Insert(int val) {
    int rank = Rank(root, val);
    pair<Node*, Node*> temp = Split(root, rank);
    Node* nod = new Node(val);
    root = Merge(temp.first, nod);
    root = Merge(root, temp.second);
}

void Remove(int val) {
    int rank = Rank(root, val);
    pair<Node*, Node*> t1 = Split(root, rank), t2 = Split(t1.first, rank - 1);
    root = Merge(t2.first, t1.second);
    delete t2.second;
}

int n;

int main() {
    scanf("%d", &n);
    for (int i = 1, opt, x; i <= n; i++) {
        scanf("%d %d", &opt, &x);
        switch(opt) {
            case 1: Insert(x); break;
            case 2: Remove(x); break;
            case 3: printf("%d\n", Rank(root, x - 1) + 1); break;
            case 4: printf("%d\n", FindKth(x)); break;
            case 5: printf("%d\n", GetPre(root, x)); break;
            case 6: printf("%d\n", GetSuc(root, x)); break;
        }
    }
    return 0;
}

普通版

// luogu-judger-enable-o2
#include <cstdio>
#define min(x,y) ((x)<(y)?(x):(y))
#define max(x,y) ((x)>(y)?(x):(y))

const int INF = 2147483647;

int Rand() {
    static int seed = 39444;
    return seed = (((seed ^ 1433223) + 810872ll) * 19260817ll) % 2147483647;
}

struct Node{
    Node *child[2];
    int val, key, size;
    
    Node(int val):val(val), size(1), key(Rand()) {
        child[0] = NULL; child[1] = NULL;
    }
    
    void Update() {
        size = 1;
        if (child[0]) size += child[0]->size;
        if (child[1]) size += child[1]->size;
    }
};

Node *root = NULL;

Node* Merge(Node* a, Node* b) {
    if (!b) return a;
    if (!a) return b;
    if (a->key < b->key) {
        a->child[1] = Merge(a->child[1], b);
        a->Update();
        return a;
    } else {
        b->child[0] = Merge(a, b->child[0]);
        b->Update();
        return b;
    }
}

void Split(Node *now, int k, Node *&t1, Node *&t2) {
    if (!now) {
        t1 = t2 = NULL; return;
    } 
    if (!k) {
        t1 = NULL; t2 = now; return;
    }
    if (k >= now->size) {
        t1 = now; t2 = NULL; return;
    }
    int ls = now->child[0] ? now->child[0]->size : 0;
    if (ls >= k) {
        Node *temp;
        Split(now->child[0], k, t1, temp);
        t2 = now; t2->child[0] = temp; 
        t2->Update(); return;
    } else {
        Node *temp;
        Split(now->child[1], k - ls - 1, temp, t2);
        t1 = now; t1->child[1] = temp;
        t1->Update(); return;
    }
}

int Rank(Node *now, int k) {
    if (!now) return 0;
    int ls = now->child[0] ? now->child[0]->size : 0;
    if (now->val <= k) return ls + 1 + Rank(now->child[1], k);
    else return Rank(now->child[0], k);
}

int GetPre(Node *now, int k) {
    int ans = -INF;
    while (now) {
        if (now->val < k) {
            ans = max(ans, now->val);
            now = now->child[1];
        } else {
            now = now->child[0];
        }
    }
    return ans;
}

int GetSuc(Node *now, int k) {
    int ans = INF;
    while (now) {
        if (now->val > k) {
            ans = min(ans ,now->val);
            now = now->child[0];
        } else {
            now = now->child[1];
        }
    }
    return ans;
}

int FindKth(int k) {
    Node *x1, *x2, *y1, *y2;
    Split(root, k - 1, x1, x2);
    Split(x2, 1, y1, y2);
    Node *now = y1;
    root = Merge(x1, Merge(now, y2));
    return now ? now->val : 0;
}

void Insert(int val) {
    int rank = Rank(root, val);
    Node *temp1, *temp2;
    Split(root, rank, temp1, temp2);
    Node *nod = new Node(val);
    root = Merge(temp1, nod);
    root = Merge(root, temp2);
}

void Remove(int val) {
    int rank = Rank(root, val);
    Node *t11, *t12, *t21, *t22;
    Split(root, rank, t11, t12);
    Split(t11, rank - 1, t21, t22);
    root = Merge(t21, t12);
    delete t22;
}

int n;

int main() {
    scanf("%d", &n);
    for (int i = 1, opt, x; i <= n; i++) {
        scanf("%d %d", &opt, &x);
        switch(opt) {
            case 1: Insert(x); break;
            case 2: Remove(x); break;
            case 3: printf("%d\n", Rank(root, x - 1) + 1); break;
            case 4: printf("%d\n", FindKth(x)); break;
            case 5: printf("%d\n", GetPre(root, x)); break;
            case 6: printf("%d\n", GetSuc(root, x)); break;
        }
    }
    return 0;
}

posted @ 2019-01-17 14:40 Noire02 阅读(1015) 评论(0) 编辑收藏举报

刷新页面返回顶部

Noire02QwQ

In solitude, where we are least alone. ——Lord Byron "Childe Harold's Pilgrimage"

数据结构-FHQ Treap（也许是全网唯一一个认真给你画图解的）

平衡树-FHQTreap

树的结点

基本操作（一）——分裂Split

功能

拆解步骤

情况一

情况二，与前一种相反

接下来是喜闻乐见的代码

情况（二）——合并Merge

其他操作：查Rank，前驱，后继

基于Split和Merge的操作：插入、删除、查找第k小

插入：查一下新数的rank，然后拆成 <rank 和 >=rank 两部分，然后把新结点与它们合并

删除：查rank，拆出rank个，t1中拆出rank - 1个，把中间那个删掉，剩下的拼回去

查第k小：拆出k - 1个，t2中拆出1个，返回中间那个结点的值，最后拼回去

最后，模板题完整代码

公告