浅谈树链剖分
update in 2024.4.17 算是大力整改了一下,这是两年的事情了!
update in 2024.4.18 补充了长链剖分内容。
重链剖分
\(\frac{12}{20}\),差不多得了,要一模了。
学习发现它的本质,是多么有趣的一件事情啊!
树剖里面最常用的其实就是重链剖分。
其实就是把序列的问题,拍到了树上,就是序列支持的操作,如区间加,区间推平,区间查询啥的。
你真的熟练掌握线段树了吗?我在写的时候就发现自己原来不是很掌握/ng/ng。
首先我们先要引出一些概念:
1.重儿子:对于一个节点之中子树最大的儿子
2.轻儿子:对于一个节点中除重儿子外的其他儿子。
3.重边:对于一个节点链接重儿子的那一条边。
4.轻边: 对于一个节点链接轻儿子的那一条边。
5.重链:由若干条重边和重儿子组成的一条链。
给出一个例图:
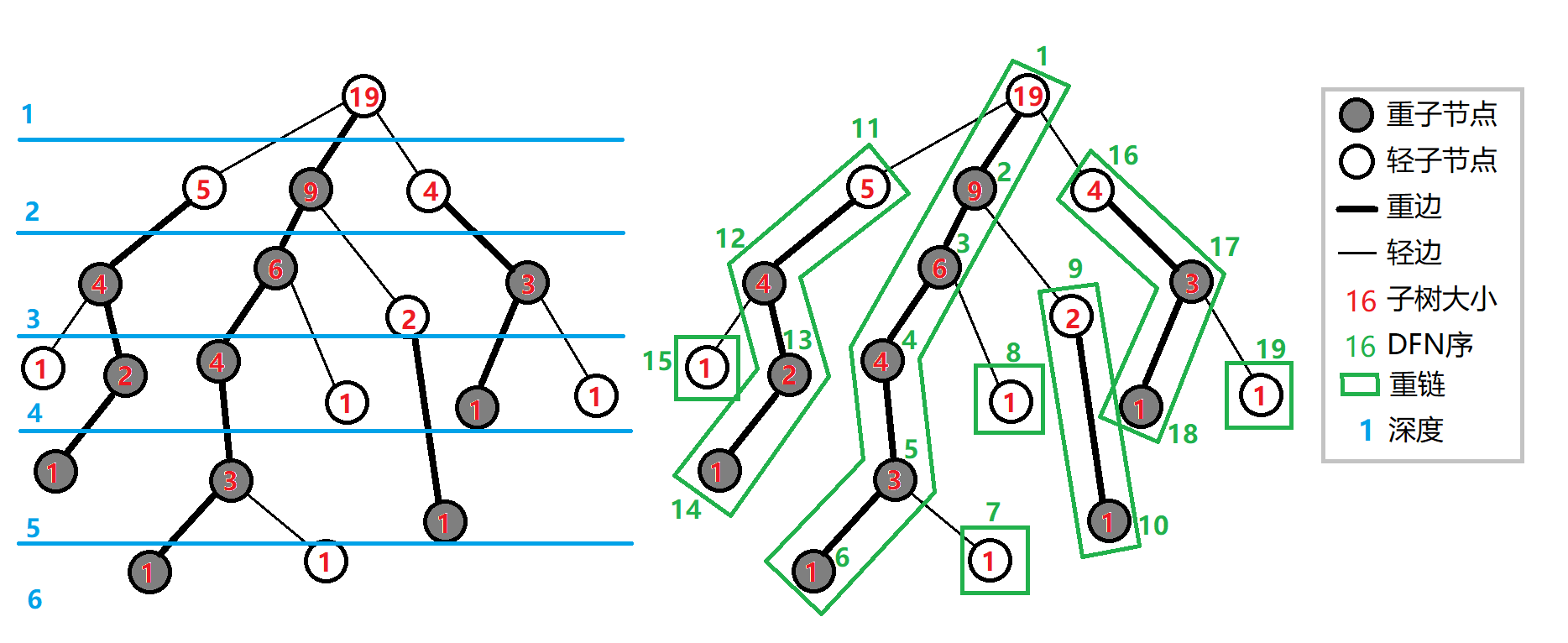
看完这个图,可以更好地理解这些概念。
剖分,其实就是指把树剖分成一条条链,满足链上点 dfn 连续。
我们用两个 dfs 完成对这个对这个树的预处理。
对于第一个 dfs 我们需要维护当前节点的重儿子,子树大小,深度,节点父亲。
void dfs1(int node,int fath)
{
siz[node]=1;//初值当前节点字数大小为1
son[node]=-1;//初始时先设没有重儿子
for(int i=1;i<g[node].size();i++)
{
int pre=g[node][i];
if(pre==fath)
continue;
fa[pre]=node;//自己儿子的父亲就是自己
dep[pre]=dep[node]+1; //节点深度等于父节点深度+1
dfs1(pre,node);
siz[node]+=siz[pre];//当前子树大小应加上儿子子树大小
if(son[node]==-1||siz[pre]>siz[son[node]])
//前一个指如果重儿子没有更新的话,先选当前的为基准
//第二个是打擂台,现在儿子的子树大小优于父节点的重儿子的子树大小
son[node]=pre;
}
}
对于第二个 dfs,我们要求出 dfn 序,以及每个节点对应的链顶编号。
具体还是看代码:
void dfs2(int node,int t)// t表示当前节点的链顶编号
{
top[node]=t;
dfn[node]=++res;//dfn序,res即遍历顺序
if(son[node]==-1)//如果当前节点没有重儿子
//也就是叶子节点
return ;
dfs(son[node],t);//往下遍历重儿子 对于他的链顶,就是其父亲的链顶
for(int i=0;i<g[node].size();i++)
{
int pre=g[node][i];
if(pre!=fa[node]&&pre!=son[node])//对于所有的轻边,我们就新开一条链给他
dfs(pre,pre);//链顶就是自己
}
}
看到这里你就大概可以明白了,就是用 dfn 序预处理出每个节点的顺序,因为对于每一条链上面的点,其 dfn 必然是连续的。(根据搜索的性质)这样就可以把树上的操作很好的转换在序列上了。
做一点补充说明,其实在开始学的时候我也有这样的问题。
就是,树剖为什么一定要按照重儿子先编号的这样一种编号方式,其他能保证编号连续把树“剖分”的方式也不行吗?
其实是为了保证时间复杂度能在 \(O(\log)\) 级别。
因为每次选择走一条轻边的时候,所在的子树 \(v\) 大小会至少除以 \(2\)(至少会有一条重边来摊)。
所以把树上的路径看成从 LCA 不断往下走的话,走过的链的数量,就是 \(O(\log)\) 级别的,我们不关心重边,因为他肯定会和 \(x,y\) 两者之一在同一条链上。
所以在树剖跳的过程中,轻边决定了时间复杂度的正确。
假设我们给出点 \(x,y\),求 LCA。
思路:跳跳跳。
-
每次我们都选择链顶深的跳,因为这样是防止跳过了
LCA,我们可以证明,跳深的是绝对不会跳过lca,就固定LCA,然后分两个点在重链和非重链上讨论即可。 -
最后当两个点都跳到同一条链的时候,深度小的就是
LCA。
发现了吗,其实这个思路和倍增差不多的,都是简化跳的次数(一段段跳)来解决问题,因为直接一步一步跳是 \(O(n)\) 的。
它是如何维护出来序列的问题。
在跳的时候,我们其实就已经把 \(x,y\) 中间的路径走过一遍了。
- 树上的两点路径是惟一的。我们每次跳都跳到当前的链顶,可以把这一段的和求出来。因为
dfn连续,这其实就是一个序列上的问题。
其实就是在跳的时候多段的答案拼起来,而这刚好又是在编号连续,所以能用数据结构的一种东西。
跳是一只 \(\log\),查询也是一只 \(\log\),所以树剖就是一个 \(O(n \log^2 n)\) 的状物。
int gsum(int x,int y)
{
int res=0;
while(top[x]!=top[y])//如果不在同一条链上
{
if(dep[top[x]]<dep[top[y]])// 选深的
swap(x,y);
res+=getsum(dfn[top[x]],dfn[x],1,n,1);//加上跳的这一段的和
x=fa[top[x]];//往上跳
}
if(dep[x]>dep[y])//由浅到深加
swap(x,y);
return res+=getsum(dfn[x],dfn[y],1,n,1);
}
剩下的基本就是线段树的操作了。
做题的时候,通常都是先考虑在序列上怎么做,再拓展到树上。
要求子树内的和,其实有一个很显然的性质,\(u\) 为根的子树,在序列上其实就是 \([dfn_u,dfn_u+siz_u-1]\)。
因为根据 dfs 的性质,我们不必关心子树内怎么标号的。在出当前的 dfs(u) 的时候,标记过点一定都是 \(u\) 为根的子树的点。
关于边权转点权的一个 Trick。
其实就是变差分也在使用的,\(d_u\) 表示 \(u\) 连接它父亲的那一条边。
剩下就是线段树操作。注意要区间覆盖在先。
一样的类似题。
你不会不知道线段树的 lzytag 是表示给儿子修改的吧。
怎么还有人用 lzytag 给自己修改呢,哈哈。
其实下传和对整段 l<=s&&t<=r 的修改是类似的,两个不太可能不一样。
一遍写过,非常流畅,用时22min,调了24min。
\(01\) 序列,要你支持区间推平和区间查询 \(0/1\) 的数量。
直接做就行了吧,lzy 表示推平成 \(0/1\)。
算是一个不错的结束了?可能以后还会写 P2486 [SDOI2011] 染色?
然而并没有结束。
长链剖分
\(\frac{13}{20}\),继续。
是一种把树剖分成链的另外一种方法,比较有意思。

- 重子节点:为 \(u\) 子节点中,子树深度最大的点编号。
- 轻子节点:为 \(u\) 子节点中,除了重子节点以外的全部点。
轻/重边的定义和重链剖分类似。
- 首先有一个结论,对于一个点,往上走到根至多会经过 \(O(\sqrt n)\) 条轻边。
考虑构造这样的一棵树,一开始只有一个叶子结点,然后想要走更多的轻边,这时候我至少需要两个点拼在它的上面,才能走到这一条轻边。
以此类推(再上一层),那就需要 \(3\) 个点,\(4\) 个点......
根据 \(1+2+3+...+\sqrt n=n\) 的性质,因为每一步我们的构造是最坏的情况,所以瓶颈就是 \(O(\sqrt n)\) 了。
实现方式和重链剖分类似。
长链剖分优化树上 \(k\) 级祖先
普通的倍增可以做到 \(O(n \log n)-O(q \log n)\),但是这还不够。
我们的长链剖分可以优化到 \(O(n \log n)-O(q)\)!
首先我们预处理出来点 \(x\) 的 \(2^i\) 祖先,显然可以 \(O(n \log n)\)。
其次我们在做长链剖分的时候,对于一个链顶 \(p\),假设重链长度为 \(d\),我们直接暴力出来 \(p\) 从 \((1-d)\) 的祖先是谁。
这样做的空间复杂度和时间复杂度都没有问题,因为每个点最多属于一个重链,所以最终数量级是 \(O(n)\) 的。
如果我们找到了一个 \(i\),满足 \(2^i \le k < 2^{i+1}\) 的话,(这个可以 \(O(n)\) 预处理)。
我们从 \(u\) 先跳 \(2^i\) 到 \(u'\),然后根据重链剖分的性质,有 \(k-2^i\le 2^i \le d_{u'}\)。
因为你跳的 \(2^i\) 步是在 \(u'\) 的子树内完成的,容易发现 \(u'\) 子树的重儿子的深度必然不小于 \(2^i\)。
再加上我们最开始的预处理出 \(u'\) 向上 \([1,d_u]\) 的祖先,我们就可以在 \(O(1)\) 查询啦!
下午考试,有空再写代码吧。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号