Optimization: Unconstrained
CanChen ggchen@mail.ustc.edu.cn
为什么先看无约束问题? 因为这是最简单的问题,没有任何约束。
大多数无约束问题,是利用一阶函数确定一个下降方向,然后搜索对应的最优步长因子,称之为一维搜索。
非精确一维搜索
一维搜索分成精确一维搜索和非精确一维搜索。其中精确一维搜索,也不是精确的,是通过黄金分割法,插值法等方法近似的。
这里重点说说非精确一维搜索。作者主要介绍了Goldstein条件:
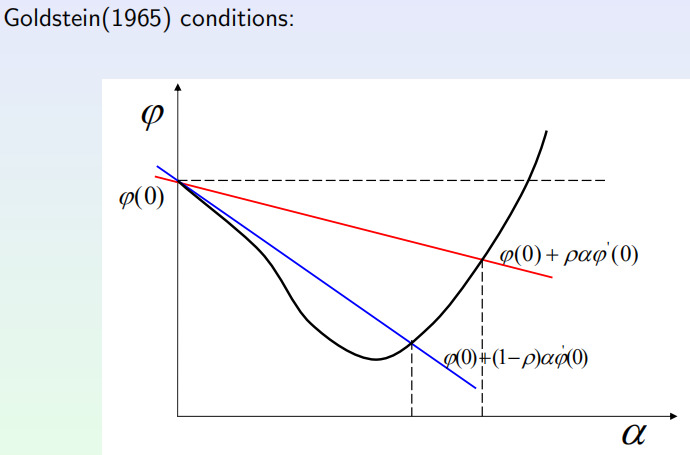
以及Wolfe-Powell条件:
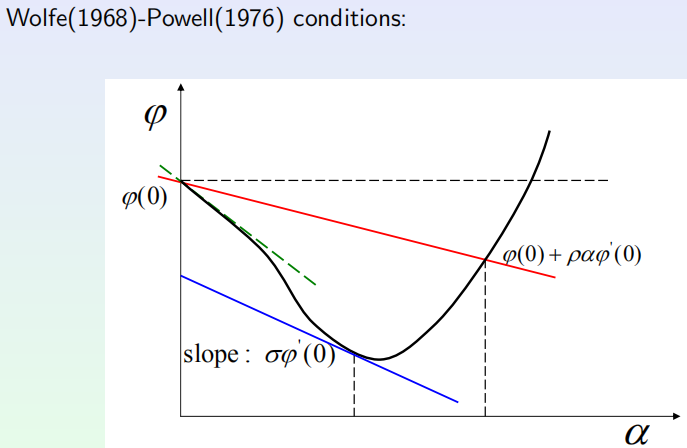
对于Wolfe-Powell条件,作者给了详细的算法迭代,最主要的思想类似于左右指针往中间靠,逼近最优解。
信頼域方法
一维搜索本质上是先确定方向,再确定步长。信頼域方法就是在当前点近似二次函数,同时确定方向和步长,注意这里不是简单的二次型函数,而是在一定半径--即信頼域下的最优二次型函数问题。所以我们同时也要更新信頼域半径。
这里最重要的就是求解信頼域子问题,老师给了个引理,就是Cauchy点在信頼域外,就取信頼域半径上Cauthy方向的点;牛顿点在信頼域里面,那么就取牛顿点;否则,取Cauchy点和牛顿点连线,与圆周的交点。
全局最优解和全局收敛性
全局最优解是指找到了这个问题在定义域里最好的解,而全局收敛性是指从定义域任意初始点出发,都能找到最优解或者稳定解。
全局收敛性定理
最速下降法
d用一阶导,然后用一维搜索确定步长,就是最速下降法。最速下降法的产生点列的所有驻点都是聚点。
关于有趣的牛顿法
f是二阶可微实函数,对f做二阶泰勒展开近似,求最小值,即能得到牛顿方向,牛顿方向的步长是1。
牛顿法收敛定理
把x*和xk放进Lip条件,然后利用x和x*足够近的这个特点,证明G(x)和G(x*)足够近,而G(x*)是正定阵,所以G(xk)的逆是有界的。
这里的lip条件相当于给G加了一阶bound,给f加了三阶bound.

牛顿收敛定理主要是说明了在最优点附近,能以二阶速度快速收敛。
针对牛顿收敛定理对算法作的改进
步长的改进--阻尼牛顿法
步长不用1,而是用一维搜索确定
下降方向的改进
牛顿法的推导是依赖于G的正定性,但是实际迭代过程中H不一定满足正定性。老师的列举的两种比较naive的方法:一种是符合下降条件就用牛顿步,不符合就随机梯度下降;另外一种,是强行加单位阵,让G正定。
拟牛顿法
原来的牛顿法需要求二阶导,计算量大,而且还不一定存在。所谓拟牛顿法就是说用利用上次的信息,加上这次的一阶信息来近似这个二阶逆。
对称秩一矫正
这里就是用H和一阶矫正,来更新本次的H。利用上次的信息来搞这个一阶矫正。这里局限性就是,不一定能保证正定。
DFP
这里用的是二阶矫正,感觉一阶和二阶都是凑参数。这种还有个名字叫DFP。
BFGS
这个本质和DFP是一样的,但是这里是直接更新G。
共轭梯度法
牛顿法虽然厉害,赖不住计算量大,占内存等缺点。另外一种方法是共轭梯度法,这里的共轭是正交的推广。主体思想就是,我第一次迭代用随机梯度下降,后面基于前面的梯度方去构造一个关于G的共轭空间。
这里比较难的一点是,定理推导全都是基于二次型,后面有一系列的修正。而且对于一般函数,非精确一维搜索也不靠谱,所以这里有个重启动策略,每隔一段时间用随机梯度。



