感知器
- 感知器通常用下面的图形表示：
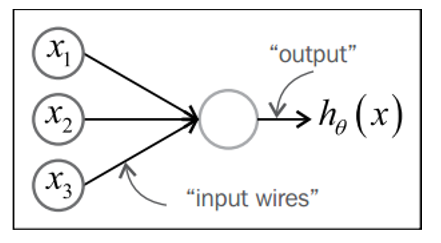
x1，x2和x3是输入单元。每个输入单元分别代表一个特征。感知器通常用另外一个输入单元代表一个常用误差项，但是这个输入单元在图形中通常被忽略了。中间的圆圈是一个计算单元，类似神经元的细胞核连接输入单元和计算单元的边类似于树突。每条边是一个权重，或者是一个参数。参数容易解释，如果某个解释变量与阳性类型（positive class）相关，其权重为正，某个解释变量与阴性类 型（negative class）相关，其权重为负。连接计算单元和输出单元的边类似轴突。
- 激励函数
感知器通过使用激励函数（activation function ）处理解释变量和模型参数的线性组合对样本分类， 计算公式如下所示。解释变量和模型参数的线性组合有时也称为感知器的预激励（preactivation）。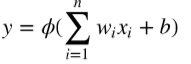
其中， ω¡是模型参数， b是常误差项， Φ()是激励方程。常用的激励方程有几种。Rosenblatt最初的感知器用的是阶跃函数（Heaviside step function或unit step function）作为激励函数。函数公式如 下所示：
如果加权解释变量的和加上常误差项之和大于0，则激励方程返回1，此时感知器就把样本归类为阳 性。否则，激励方程返回0，感知器就把样本归类为阴性。阶跃函数图形如下所示：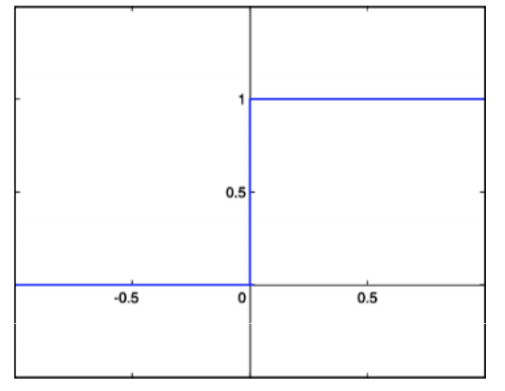
另一个常用的激励函数是逻辑S形（logistic sigmoid ）激励函数。这个激励函数的梯度分布可以更有 效的计算，在处理后面的ANN算法时十分有效。其计算公式如下：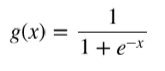
其中， x是加权输入的和。这个模型与第四章的逻辑方程类似，是解释变量值与模型参数的线性组合，与逻辑回归模型是一样的。虽然用逻辑S形激励函数的感知器与逻辑回归是一样的，但是要估计 的参数不同。
