非线性模型的回归和分类问题——决策树

• 问题选择

　　用熵（entropy）来度量信息的不确定性。 以比特（bits）为计量单位，熵量化了一个变量的不确定性，熵计算公式如下所示：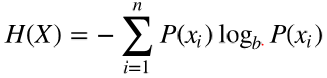

　　例如，一个硬币投掷一次事件发生后一般有两种可能：正面或反面。正面朝上的概率是0.5，反面朝 上的概率也是0.5。那么一个硬币投掷一次的结果这个变量的熵：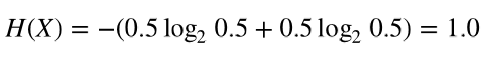

　　也就是说，两个等概率的可能值，正面和反面，只需要一个比特。如果是两个硬币投掷一次事件发生 后一般有四种可能：正面正面，正面反面，反面反面，反面正面，每种可能的概率是0.25。其熵为：

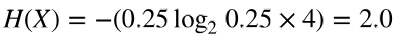
　　如果硬币的两面相同，那么表示其可能值的变量熵为0比特，也就是说，结果是确定的，变量再也不 会产生新信息量了。熵还可以用小数值表示。比如，一个不正常的硬币，其正反面的材质不同，一边 重一边轻。导致其投掷后正面朝上的概率0.8，反面朝上概率0.2。那么其熵为：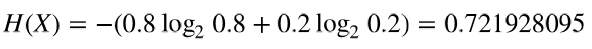

一个不正常的硬币投掷后其结果的熵是一个小数。虽然两种结果都有可能，但是因为其中一种可能性 更大，所有不确定性减小了。

• 信息增益（information gain）

计算公式如下：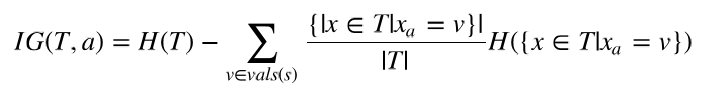

 

• 基尼不纯度（Gini impurity）

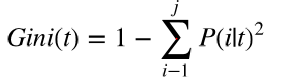
• 决策树集成

随机森林（random forest）