线性回归
参考资料:Mastering Machine Learning with scikit-learn
- 广义线性回归模型之一元线性回归,多元线性回归和多项式回归—回归任务
回归问题的目标是预测出响应变量的连续值
- 一元线性回归
一元线性回归假设解释变量和响应变量之间存在线性关系
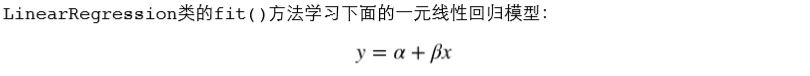
一元线性回归拟合模型的参数估计常用方法是普通最小二乘法(ordinary least squares )或线性最小 二乘法(linear least squares)
- 带成本函数的模型拟合评估
成本函数(cost function)也叫损失函数(loss function),用来定义模型与观测值的误差。模型预测的价格与训练集数据的差异称为残差(residuals)或训练误差(training errors)。模型预测的价格与测试集数据的差异称为预测误差(prediction errors)或测试误差(test errors)。
模型的残差是训练样本点与线性回归模型的纵向距离,如下图所示:
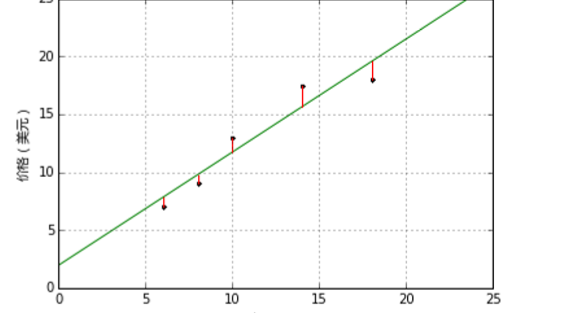
通过残差之和最小化实现最佳拟合,也就是说模型预测的值与训练集的数据最接近就是最佳 拟合。对模型的拟合度进行评估的函数称为残差平方和(residual sum of squares)成本函数。就是 让所有训练数据与模型的残差的平方之和最小化,如下所示: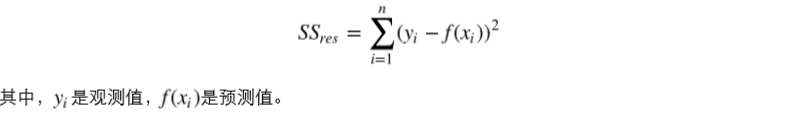
- 解一元线性回归的最小二乘法
通过成本函数最小化获得参数。按照频率论的观点,我们首先需要计算x 的方差和x 与 y的协方差。
方差是用来衡量样本分散程度的。如果样本全部相等,那么方差为0。方差越小,表示样本越集中, 反正则样本越分散。方差计算公式如下: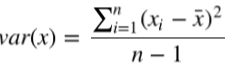
协方差表示两个变量的总体的变化趋势。如果两个变量的变化趋势一致,也就是说如果其中一个大于 自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变 量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之 间的协方差就是负值。如果两个变量不相关,则协方差为0,变量线性无关不表示一定没有其他相关 性。协方差公式如下: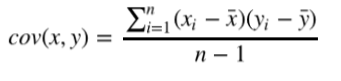
有了方差和协方差,就可以计算相关系统 β了
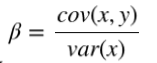
计算 α
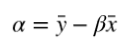
这样就通过最小化成本函数求出模型参数了。
- 模型评估:R方(r-squared)
R方也叫 确定系数(coefficient of determination),表示模型对现实数据拟合的程度。
首先,计算样本总体平方和:
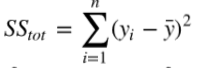
然后,计算残差平方和:
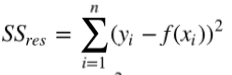
计算R方: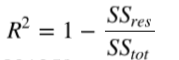
R方表示可以由模型解释的数据集的比例。
- 多元线性回归
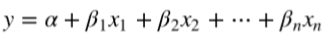
写成矩阵形式如下:
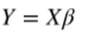
一元线性回归可以写成如下形式:
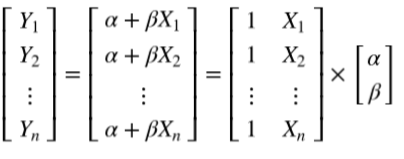
- 多项式回归
多项式回归可以用来构建非线性关系模型
二次回归(Quadratic Regression),即回归方程有个二次项,公式如下:
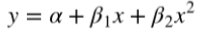
PolynomialFeatures转换器可以用来实现曲线关系
from sklearn.preprocessing import PolynomialFeatures
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression() regressor_quadratic.fit(X_train_quadratic, y_train)
使用更高阶的多项式回归会出现过度拟合,这样的模型并没有从输入和输出中推导出一般的规律,而是记忆训练集的结果,这样在测试集的测试效果就不好了。
- 正则化
正则化(Regularization)是用来防止拟合过度的一种方法,就是用最简单的模型解释数据。
1.岭回归(Ridge Regression,RR, 也叫Tikhonov regularization),通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法。岭回归增加L2范数项来调整成本函数(残差平方和):
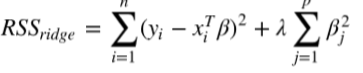
λ是调整成本函数的超参数(hyperparameter),不能自动处理,需要手动调整一种参数。 λ增大,成本函数就变大。
2.最小收缩和选择算子(Least absolute shrinkage and selection operator, LASSO),增加L1范数项来调整成本函数(残差平方和):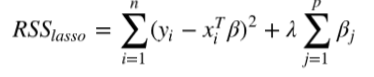
LASSO方法会产生稀疏参数,大多数相关系数会变成0,模型只会保留一小部分特征。而岭回归还是 会保留大多数尽可能小的相关系数。当两个变量相关时,LASSO方法会让其中一个变量的相关系数 会变成0,而岭回归是将两个系数同时缩小。
3.弹性网(elastic net)正则化方法,通过线性组合L1和L2兼具LASSO和岭回归的内容。
- 梯度下降法拟合模型
前面的内容都是通过最小化成本函数来计算参数的:
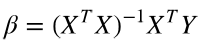 这里X是解释变量矩阵,当变量很多(上万个)的时候, XTX计算量会非常大。另外,如果XTX 的行列式为0,即奇异矩阵,那么就无法求逆矩阵了。这里介绍另一种参数估计的方法,梯度下降法(gradient descent)。拟合的目标并没有变,还是用成本函数最小化来进行参数估计.
这里X是解释变量矩阵,当变量很多(上万个)的时候, XTX计算量会非常大。另外,如果XTX 的行列式为0,即奇异矩阵,那么就无法求逆矩阵了。这里介绍另一种参数估计的方法,梯度下降法(gradient descent)。拟合的目标并没有变,还是用成本函数最小化来进行参数估计.
梯度下降法的一个重要超参数是步长(learning rate)
如果按照每次迭代后用于更新模型参数的训练样本数量划分,有两种梯度下降法。批量梯度下降 (Batch gradient descent)每次迭代都用所有训练样本。随机梯度下降(Stochastic gradient descent,SGD)每次迭代都用一个训练样本,这个训练样本是随机选择的。当训练样本较多的时 候,随机梯度下降法比批量梯度下降法更快找到最优参数。批量梯度下降法一个训练集只能产生一个结果。而SGD每次运行都会产生不同的结果。SGD也可能找不到最小值,因为升级权重的时候只用 一个训练样本。它的近似值通常足够接近最小值,尤其是处理残差平方和这类凸函数的时候。
from sklearn.linear_model import SGDRegressor
regressor = SGDRegressor(loss='squared_loss')
regressor.fit_transform(X_train, y_train



