从带权二分到闵可夫斯基和与凸生成函数
写于 whk 时期,虽然开始 whk 之前就想写了,不过一直没时间。
不过 whk 这边让我学会了灵活的往时间轴里塞东西。
所以虽然我更忙了,但是我更有空了。
不说废话了。
由于在碎时间下写出,所以可能会有很多冗杂的细碎说明,主要是记录了思考过程中想了很久的点。
坏处是文章变得冗长,好处是如果你的思路卡在某个点上,不妨看看本文。
我在网上并未查阅到有人对闵可夫斯基和极为细致的阐释,也没有看到有人称其为生成函数,但偶然的一次代码查阅中我看到有人称其为 poly,有感而发写就本文。
首先看到有很多争议的凹凸函数定义,本文采取主流观点,若使用凹凸区分函数,则凸函数开口朝上(与文字的弯曲方向相反),若使用上凸与下凸来区分函数,则下凸函数开口朝上。
(真的不理解为什么凹凸的函数图像和文字是反的。)
不如我们把形如 \(\cup\) 的凸包称为 \(\min\) 包,将形如 \(\cap\) 的凸包称为 \(\max\) 包。
目录:
- 带权二分
- 基于费用流模型的凸性
- 整体带权二分
- 例题部分
- 闵可夫斯基和
- 例题部分
- 与带权二分间的联系
- 与生成函数间的联系——凸生成函数
- 代码模板
- 例题部分
- 课后习题
带权二分
由于本文重点是后面的闵可夫斯基和,这里仅对带权二分做概念上的介绍,细节上的部分此处不做探究。
实际利用了凸函数的性质和二分求解。
其所求解的问题大体上形式如下:
求一个经典最值问题,但要求其中的某个量恰好为 \(k\)。
典型的例子例如最小生成树但限制与某个点相连的边数恰好为 \(k\)。
这类问题应用带权二分的条件是保证“我们取最值的量”关于“我们取 \(k\) 的量”是一个凸函数。
在 \(\text{OI}\) 中,函数的凸性通常难以证明,一般靠猜结论 + 打表验证的方式来获得结论。
根据定义,凹凸函数的导数是单调的,而在离散的数组中,这反映为差分数组是单调的,验证凸性通常需要用到。
说了这么多,那么我们如何来利用这个凸性呢?
当然一般我们求不出这个凸函数的所有值(要不然那就能直接得出答案了)。
我们应用的性质是:将凸函数加上一个一次函数,其顶点会偏移,但其仍保持凸性。
准确的说,将凸函数 \(f(x)\) 加上 \(-kx\) 得 \(f(x)-kx\) 的顶点横坐标 \(x_0\) 满足 \(f'(x_0)=k\)(即原函数在 \(x_0\) 处的斜率为 \(k\)),理解可以认为 \(k+(-k)\) 刚好等于 \(0\),于是成为顶点。
举个例子的话,最小生成树关于某个点的度数可以证明是凸的,但我们一般求最小生成树的算法只能求出真正的“最小生成树”,也就是不做度数限制的答案。
换句话说,我们求的是凸函数的顶点。
有了顶点纵坐标我们通常能顺便求出横坐标,但关键的问题就是,这个横坐标不等于 \(k\)。
这个时候我们就可以将凸函数加上一次函数来做偏移,你求解一般问题的算法中通常可以比较轻松地实现“每个特殊值的权值都增加 \(x\)”。
在上述问题中,我们每选一条我们要限制度数的边就将答案额外加上 \(x\)(也就相当于它们的边权增加了 \(x\)),那么我们观察图像,横坐标为 \(i\) 的所有点都加上了 \(ix\),也就相当于给凸函数加上了一个一次函数。
尽管你还是不知道这个凸函数长啥样,但你能求顶点以及顶点的横坐标。
这就像一个黑盒子,你每次偏移,盒子告诉你偏大了偏小了,于是就可以应用上二分算法来求解。
关于带权二分的细节:
- 在答案为整数时你可以使用整数二分,这是因为斜率是整数,否则你必须使用小数二分。
- 输出时请减去 \(kx\) 而不要减去 \(k_{\rm true} x\),后者 \(k_{\rm true}\) 表示计算过程中算出来的 \(k\),这是因为如果有多个值是同一斜率,这会导致 \(k_{\rm true}\ne k\),但此时我们减去 \(kx\) 仍然是能得到正确答案的。
这是朴素的带权二分部分。
需要额外注意的一点是如果我们的 check() 部分能写成 \(\text{dp}\) 的形式那么可以把本题看作一个 \(\text {dp}\) 凸优化。
选中恰好 \(k\) 个不相交的非空子区间这种一看就是 \(\text{dp}\),那带度数限制的最小生成树呢?
我们可以把被度数限制的点之外的所有点做一个最小生成树,则剩余的部分为一个树形 \(\text{dp}\)。
这通常适合我们打表验证凸性,我们可以自然地在 \(\text{dp}\) 中加一维 \(k\) 表示我们限制的参数,转移形如 \(f_{k_1,S}\cup f_{k_2,T}\to f_{k_1+k_2,S\cup T}\)。
这个 \(\text{dp}\) 在之后的闵可夫斯基和部分会用到。
说句题外话,带权二分对于斜率有相等的凸函数的处理方式极为麻烦,如果你真的遇到了难以处理的情况,可以使用下面会讲到的闵可夫斯基和。
以及比较恶心的带权二分构造解,我认为该算法的恶心程度上限可以与计算几何并列。
基于费用流模型的凸性
这不是什么算法,而是关于观察凸性的技巧。
虽然果断打表一般是最优解,但对于暴力不是特别好写或者一眼就能看出来费用流模型的,直接应用还是能省不少时间。
费用流模型指的是一张边有流量和费用的图,有源点和汇点,设由源点向汇点流恰好为 \(k\) 流量的最大(最小费用)为 \(f_k\),则 \(f_k\) 是凸的。
若一个问题能规约到费用流模型上,则其天然具有凸性。
整体带权二分
如果题目仅仅要求的是 \(k\in[1,n]\) 的所有答案,我们可以套上一个整体二分。
整体二分具有一定的局限性,它要求 check 的复杂度与区间长度成正比。
以带度数限制的最小生成树为例,我们的 check 就要写成仅仅递归不确定的边,可以证明每条边至多只会向一侧递归。
复杂度 \(\Theta(n\log^2n)\) 且通常带有巨大常数。
这东西没例题,或许可以用下面的闵可夫斯基和例题来练习。
优势是可能稍微好写好想一点。
如果你发现这个带权二分实际上解决的是 \(\text{dp}\) 问题,那么你可以应用上下面介绍的这种能在 \(\Theta(n\log n)\) 的复杂度内解决上述问题的方法。
例题部分
P2619 [国家集训队] Tree I
给定一张带权图,每条边有黑白,要求恰好选出 \(k\) 条白边前提下的最小生成树。
\(m\le 10^5\)。
较为经典的题目。
凸性证明好像比较困难?
不过看了刚刚的内容本题应该没什么可讲的。
稍有蹊跷的是该问题似乎难以用 \(\text{dp}\) 实现。
这类题目令人头疼的点在于其凸性无法大范围验证,因为暴力似乎是指数级别的。
代码。
CF739E Gosha is hunting
做 \(n\) 件事情,你有 \(a\) 次 \(A\) 能力和 \(b\) 次 \(B\) 能力,第 \(i\) 件事情使用 \(A\) 能力成功率是 \(p_i\),使用 \(B\) 能力成功率是 \(u_i\),一件事可以同时使用 \(A,B\) 能力,都干成功算成功一次。
问最大期望成功事件数量。
\(n\le 10^3\)。
Ex:\(n\le 10^5\)。
如果只有一个能力我们显然是可以贪心选的。
我们可以带权二分 \(A\) 能力,也就是每多选一个 \(A\) 能力就把答案减 \(k\),这样我们在这一维就可以贪心选。
然后就可以 \(dp_{i,j}\) 表示前 \(i\) 个事件里用了 \(j\) 次 \(B\) 能力,\(\Theta(n^2\log n)\)。
你发现既然选 \(A\) 是没有限制的,那一个人从不选 \(B\) 到选 \(B\) 的答案增量就是定值 \(\max(p_i+u_i-p_iu_i-k,u_i)-\max(0,p_i-k)\)。
把这些排个序取前 \(b\) 大加上即可做到 \(O(n\log n)\) 的 check,总复杂度 \(O(n\log^2 n)\)。
代码。
P4383 [八省联考 2018] 林克卡特树
给定一棵树,你需要恰好删掉 \(k\) 条边然后连上 \(k\) 条 \(0\) 边形成一棵新树,问新树中两点距离和最大是多少。
\(n\le 3\times 10^5\)。
首先把题目转化成选择 \(k+1\) 条无交链使得权值和最大。
然后设 \(\text{dp}\) 状态,\(f_{x,k,0/1/2}\) 表示 \(x\) 子树,子树总共选了 \(k\) 条链,最终选出的图形在 \(x\) 点有 \(0/1/2\) 个度数。
上面是不连 \(w_{x\to y}\),下面是连 \(w_{x\to y}\)。
初始值 \(f_{x,0,0}=f_{x,1.2}=0,f_{\text{others}}=-\infty\),\(f_{x,1,2}=0\) 表示的是一个节点本身可以视为一条链,相当于连了一个自环不能往外拓展。
代码。
闵可夫斯基和
Minkowski Sum。
闵可夫斯基和的形式化定义是对于两个全凸包(\(\min\) 包或 \(\max\) 包有类似的定义)\(A,B\),\(A+B\) 定义为 \(\{x+y|x\in A,y\in B\}\) 构成的全凸包。
其有很优美的性质。
偷个图:
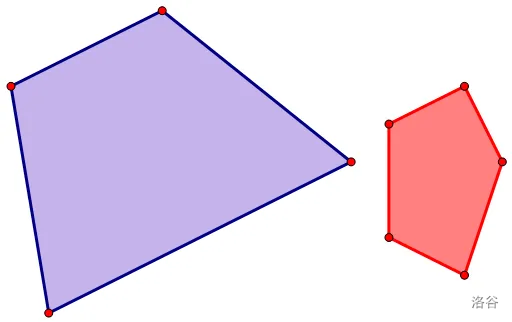
将上图的红蓝凸包做完闵可夫斯基和即为:
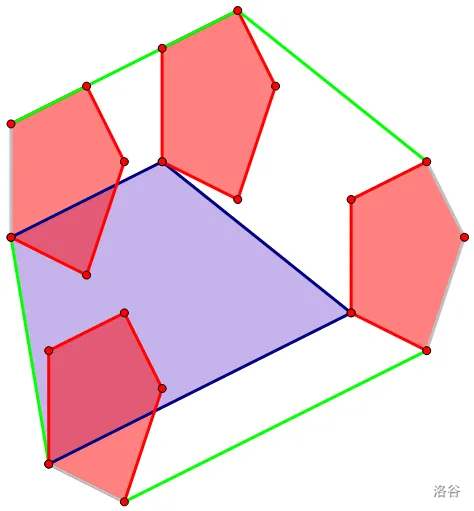
如果我们仔细观察构成这两个凸包的那些边,你发现将它们按斜率排序后顺次相连组成的新凸包正是它们的闵可夫斯基和。
其实是不难理解的,对着图蹬一会儿就理解了。
由于凸包上边的有序性,我们要做的形如线性地归并两个有序的数组。
这往往揭示着更深刻的意义。
如果我们将全凸包类似的改为上下凸包,则我们求出新凸包的方法大体不变。
但我们发现:将两个 \(\min\) 凸数组做 \((\min,+)\) 卷积,则可以线性完成。
(\(\max\) 凸数组与 \((\max,+)\) 卷积同理。)
例题部分
P4557 [JSOI2018] 战争
在平面直角坐标系上,给出两个点集 \(A,B\),\(q\) 次询问,每次给出一个向量 \(\vec x\),问将 \(A\) 集合构成的凸包整体平移 \(x\) 与 \(B\) 集合是否有交。
\(n,q\le 10^5\)。
喜闻乐见的计算几何,由于在当前 \(\text{OI}\) 界并非主流考察或学术点,这里仅涉及思路,代码就不给了(其实是因为我不会写)。
把判定式写出来:\(a+\vec x=b(a\in A,b\in B)\),变形得 \(\vec x=b-a(a\in A,b\in B)\),也就是说我们求出 \(B\) 和 \((-A)\) 做闵可夫斯基和构成的凸包,每次判定 \(x\) 是否在其中即可。
但闵可夫斯基和并不全是计算几何的产物,其可以应用于我们许多平凡的最值问题。
P9962 [THUPC 2024 初赛] 一棵树
给定一棵树,你需要将 \(k\) 个点染成黑色,最小化每条边两边黑点数的差的和。
即令第 \(i\) 条边两边的黑点数之差为 \(s_i\),最小化并求出 \(\sum\limits_is_i\)。
\(n\le 5\times 10^5\)。
其实对两个凸包做 \((\min,+)\) 卷积并不一定要真的笨重地手动归并两个差分数组,本质其实是合并两个可重集,我们可以使用比较厉害的平衡树 + 启发式合并,线段树合并,以及更为厉害的 \(\Theta(\log n)\) 可并堆。
(因为有时候我们还要对凸包做一些差分数组区间加之类的奇怪东西。)
一点题外话是我参加 APIO2023 前刚接触分层图最短路还没开始学就被创死了,这次参加 THUPC2024 前刚接触 Minkowski Sum 还没开始整理就似了。
可以说是官解的细化吧。
首先有朴素的树上背包,设 \(f_{x,i}\) 为子树 \(x\) 中染了 \(i\) 个黑点,该子树(包括根向上连的那条边)的权值最小值。
转移式很简单,首先合并子树 \(f_{x,i}+f_{y,j}\to f_{x,i+j}\),就是做了一个 \((\min,+)\) 卷积。
然后把所有子树合起来之后如果 \(x\ne 1\),那再加上根选或不选的代价,设 \(g_i\) 为子树内选了 \(i\) 个黑点的代价,则有 \(g_i=|i-(k-i)|=|2i-k|\)。
也就是合并结束之后 \(\forall i,f'_{x,i}\gets \min(f_{x,i}+g_i,f_{x,i-1}+g_i)\)。
以上就是 \(\Theta(n^2)\) 的 \(\text{dp}\) 部分,我们考虑优化。
\((\min,+)\) 卷积想要优化只有一个思路,考虑证明 \(f_x\) 关于 \(i\) 是凸的。
事实上不妨假设儿子的 \(f_{y}\) 都是凸的,如果经过合并之后能证明 \(f_x\) 也是凸的,则我们能归纳地证明这个问题。
既然假设 \(f_y\) 是凸的那么对其做 \((\min,+)\) 卷积就是求闵可夫斯基和,也就是将两个单调有序的差分数组归并起来,所以合并后仍为凸函数。
然后我们加上 \(x\) 是否染黑的代价,也就是:
那我们可以进一步拆解,先 \(f'_{i}\gets \min(f_i,f_{i-1})\),再 \(f'_i\gets f_i+g_i\)。
前一个操作可以看作往背包里扔了一个空元素,后一个操作是凸函数加凸函数,仍然是一个凸函数(证明就是单调导数相加仍单调)。
好知道 \(f_x\) 是凸的了,那么前一部分合并就处理完了,现在只需要处理 \(f_i'\gets f_i+g_i\)。
考虑维护 \(f,g\) 的差分数组 \(F,g'\),则我们发现:
(\(g'\) 是 \(g\) 的差分数组。)
所以这对 \(F\) 的影响就是值域上一段前缀向左挪 \(2\),中间可能有一个值不变,后面的部分向右挪 \(2\)。
(实际上对差分数组的第一个数的增加并不是 \(-2\) 而是 \(k\),但这不影响我们的合并过程,我们可以将其留到最后加到答案中。)
考虑 \(F\) 还需要支持快速合并,直接上能打 tag 的可并对顶堆,复杂度 \(\Theta(n\log n)\)。
(也可以平衡树 + 启发式合并,多一只 \(\log\)。)
代码。
与带权二分间的联系
闵可夫斯基和通常可以在与带权二分相同的复杂度内对每个 \(k\in[1,n]\) 解决问题,利用了带权二分的凸性。
刚刚看到这个的时候可能比较难以理解,我们细化到过程中:
首先你需要把带权二分的求极值过程写成 \(\text{dp}\) 的形式,不妨我们假设状态 \(f_S\) 可以近线性求出凸包顶点。
由上可知,我们只需要多开一维状态 \(f_{S,k}\)(\(k\) 表示我们限制的量使用了几个)就可以以错误的复杂度求出所有答案。
那我们将 \(f_{S,k}\) 视为一个函数 \(f_S(k)\),既然该问题可以使用带权二分解决,则 \(f_S\) 必然具有凸性。
我们又知道两个 \(\text{dp}\) 状态合并时 \(k\) 这一维上通常做了 \((\min/\max,+)\) 卷积,那我们使用闵可夫斯基和的方式来合并,通常就可以降低复杂度。
(前提是这个 \(\text{dp}\) 在最终并没有用什么奇怪数据结构优化,是一个正常的 \(\text{dp}\) 形式。)
那合并 \(\text{dp}\) 状态的过程通常形如一棵树,例如 \(\forall i\in[2,n],f_i\gets f_{i-1}\cup a_i\) 就是这种树结构:
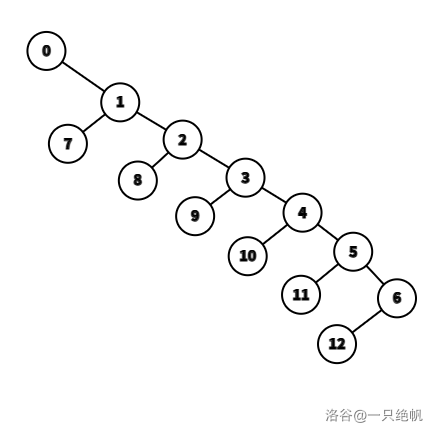
亦或是你直接在一棵树上进行 \(\text{dp}\),每次将儿子的数组合并起来。
闵可夫斯基和对这两种形式都可以处理,见之后的例题部分。
与生成函数的联系
有意思的一点是,若将闵可夫斯基和记作 \(+\),将凸包的取 \(\max\) 记作 \(\text{or}\)(前提是根据某种性质可以证明取完 \(\text{or}\) 仍然为凸包),那么 \(+\) 关于 \(\text{or}\) 是具有分配律的,即 \(a+(b\operatorname{or}c)=a\operatorname{or}b+a\operatorname{or}c\)。
换句话说其实关于 \((+,\text{or})\) 的矩阵乘法是具有结合律的。
不过这没什么用,随着运算量的增加,我们的凸包大小会急剧上升,对其做一些类似矩阵快速幂的东西就像对不取模的 \(\text{OGF}\) 做多项式一样荒谬,而对一个取最值的事物去做取模也完全走不通。
但这揭示了闵可夫斯基和与生成函数的一致性,将 \(+\) 视作多项式乘法,\(\text{or}\) 视作多项式加法,多项式正好也会随着乘法而增加大小,后文的例题会提到,树上分治背包 NTT 的技巧可以直接套用于此。
很多人认为多项式很难也不考没必要学,可于其中解题时的思想火花却无比珍贵。
我认为多项式拦住我们的巨大门槛是 与实际问题没什么关系的运算实现 以及 其解决的大多是难以理解的计数类问题。
那我们不妨从凸包这类具有多项式性质但思想和代码都极其通俗的“多项式”来入门,去揭示这一类“数组”的运算。
我就不起某种抽象的名字了,不如将凸包的多项式性质写实地称为“凸生成函数”。
你想矩阵的 \((+,\times)\) 都可以拓展到 \((\min/\max,+)\) 了,那我们卷积玩家一样可以在某种程度上进行拓展。
这类基础多项式的应用有苛刻的条件:题目的性质必须满足无论如何,你所研究的问题必须在各个过程中一直保持凸性。
如果其碰巧又涉及了凸包的合并或卷积,那么我们就可以放心应用了。
由于 \(\min\) 与 \(\max\) 是对称的,所以我们下文仅讨论 \(\min\) 以及 \(\min\) 包,\(\max\) 的情况可以相应对称过去,下文称所有凸包构成的集合为 \(\mathbb T\)。
视凸包的闵可夫斯基和为乘法,则 \((\mathbb T,\times)\) 构成一个阿贝尔幺半群(有二元运算、交换律、结合律、零元、封闭性的集合)。
在实现上一般采用归并差分数组的方式,复杂度 \(\Theta(|A|+|B|)\)。
在给定意义下若我们保证对两个凸包取 \(\min\) 不改变凸性,则我们视凸包的取 \(\min\) 为加法。
该加法并不满足封闭性,但如果我们在题目的实际意义中证明出凸性不变,那我们可以近似把 \((\mathbb T,+,\times)\) 视作一个阿贝尔半环(有两个二元运算、交换律、结合律、分配律、零元、幺元、封闭性的集合)。
有些题目可能会出现两个凸包合到一起但其状态需要向左一位移动,这种情况下其 \(0\) 位置通常没有意义,可以向左一位存储,但有的时候我们碍于数字意义不想直接把意义左挪一位,所以我们有了左移和右移操作。
右移操作的本质其实就是 \(A\gets A+\{\infty,0\}\),但左移操作呢?难道我们就硬生生多了一个我们需要但如此丑陋的东西吗?
不然,我们只需将凸包引入负数下标便可解决这个问题,记 \(A_{\gets x}\) 为 \(A\) 这个凸包向左移动 \(x\) 个单位,则 \(A_{\gets 1}=A+\{\infty,0\}_{\gets 1}\)。
但负数下标使用的场合较少,同时我们可以证明 \(\forall A,B\in\mathbb T,\forall x,y\in\mathbb R,A_{\gets x}+B_{\gets y}=(A+B)_{\gets x+y}\),所以在实际应用中我们通常添加一个左移操作来弥补负数下标在编程中的不便。
代码模板
多项式写法
下面给出一般的代码实现,在实际代码中一般采用更符合直觉的 + 和 | 运算符(我们对 + 运算符通常的刻板印象并不适合让它作为取 \(\min\) 操作),这个 struct U 可能是 \(\text{OI}\) 中最形象的数据结构表示法了:
struct U:basic_string<ll> {
U() {resize(1);}
U(initializer_list<ll> x):basic_string<ll>(x) {}
U friend operator+(U a,U b) {
U c{a[0]+b[0]};
UF(i,sz(a)-1,1) a[i]-=a[i-1];
UF(i,sz(b)-1,1) b[i]-=b[i-1];
merge(a.begin()+1,a.end(),b.begin()+1,b.end(),back_inserter(c));
F(i,1,sz(c)-1) c[i]+=c[i-1];
F(i,0,sz(c)-1) c[i]=min(c[i],inf);
return c;
}
U friend operator|(U a,U b) {int d=min(sz(a),sz(b));
U c{min(a[0],b[0])};
F(i,1,d-1) c+=min(a[i],b[i]);
F(i,d,sz(a)-1) c+=a[i];
F(i,d,sz(b)-1) c+=b[i];
return c;
}
U operator<<(int x) {
U b=*this;F(i,0,sz(b)-x-1) b[i]=b[i+x];
b.resize(sz(b)-x);return b;
}
};
//(max,+)卷积就是将min改为max,同时不要忘了把operator+()里面的merge()改为:
//merge(a.begin()+1,a.end(),b.begin()+1,b.end(),back_inserter(c),greater<>());
其中 operator+ 有更精简的写法(不过我认为上面的写法更好记):
U friend operator+(U a,U b) {int n=sz(a)+sz(b)-1;
f+=inf*2,g+=inf*2;
U c{a[0]+b[0]};c.resize(n);
for(int i=1,j=0,k=0;i<n;i++)
(a[j+1]-a[j]>b[k+1]-b[k]?j:k)++,r[i]=min(f[j]+g[k],inf);
return c;
}
将 \(k\) 个大小和为 \(n\) 的凸包闵可夫斯基和起来并不能直接一个一个加起来,可以卡到 \(\Theta(n^2)\),我们可以使用分治合并做到 \(\Theta(n\log k)\) 的复杂度:
U mer=[](U A[],int n) {
for(int m=1;m<n;m<<=1) for(int i=0;i+m<n;i+=m<<1)
A[i]=A[i]+A[i+m];
return A[0];
};
若同时想保留原来的凸包数组,那么可以使用递归分治:
U mer(U A[],int L,int R) {
if(L==R) return A[L];int mid=L+R>>1;
return mer(A,L,mid)+mer(A,mid+1,R);
}
树上的凸包合并可以见下面的例题,采用轻重链分治的方式做到 \(\Theta(n\log n)\)。
计算几何写法
虽然我们一般遇不到计算几何,但有时我们是对某些向量进行闵可夫斯基和(见下方课后习题),所以我们需要掌握这种写法。
其实完全没有区别,只不过多了一个向量类而已。
struct V {
int x,y;
V operator+(V b) {return {x+b.x,y+b.y};}
V operator-(V b) {return {x-b.x,y-b.y};}
bool operator<(V b) {if(1ll*b.x*y==1ll*x*b.y) return /*1ll*x*x+1ll*y*y<1ll*b.x*b.x+1ll*b.y*b.y*/;
return 1ll*b.x*y<1ll*x*b.y;}
};
代码框中被注释的部分是需要注意的,根据不同题目对闵可夫斯基和的需要,我们在这里需要讨论应该写什么(这会在向量集转化成凸包的时候被用到),按照凸包的一般定义来说,我们认为模长大者应当被保留,所以我们在处理 \(\min\) 包和 \(\max\) 包的时候需要注意这里的修改。
其余部分与正常闵可夫斯基和完全一样。
还有将若干向量转变为凸包的方法:
U toU(U &A) {
sort(begin(A),end(A),[](V a,V b){return a.x==b.x?/*a.y>b.y*/:a.x<b.x;});
U B{A[0]};F(i,1,sz(A)-1) {
while(sz(B)>=2&&!(B[sz(B)-1]-B[sz(B)-2]<A[i]-B[sz(B)-1])) B.pop_back();
B+=A[i];
} return B;
}
同理在这里的注释部分也需要注意,如果你在上面 struct V 中写的足够完善这里可以不必讨论。
例题部分
不知道来源的板子题
给定一个长为 \(n\) 的序列,对每个 \(k\in[1,n]\) 求出恰好选 \(k\) 个不交的非空子区间,最大的元素和是多少。
\(n\le 3\times10^5\)。
往朴素里想。
我的第一想法其实是从左往右 \(\text{dp}\):\(f_{i,j,0/1}\) 表示考虑到第 \(i\) 个数,已经加了 \(j\) 段,最后一个数有/没有选。
朴素的复杂度是 \(\Theta(n^2)\) 的。
然后我们发现思路死了,这是因为我们去掉 \(j\) 这一维后并没有类似于“合并”的操作,也就利用不上闵可夫斯基和的优秀性质。
我们来看一个朴素意义下复杂度更高的做法:
\(f_{l,r,k,0/1,0/1}\) 表示在区间 \([l,r]\) 内,我们选择了 \(k\) 段,最左边一个数选了/没选,最右边一个数选了/没选。
朴素做复杂度是 \(\Theta(n^3)\) 的。
但我们把每个元素改写成一个函数 \(f_{l,r,0/1,0/1}(k)\),则我们可以验证每个 \(f(k)\) 具有凸性。
而我们合并两个大小为 \(x\) 和 \(y\) 的函数所需的时间是 \(\Theta(x+y)\)。
于是我们递归求解,每次劈成两半求出凸包后再合并,复杂度 \(\Theta(n\log n)\)。
注意这里的合并的本质其实是 \((\min,+)\) 卷积,而不是直接相加,这是闵可夫斯基和真正厉害的地方。
Gym102331J Jiry Matchings
给定一棵边带权的树,你需要对每个 \(k\in[1,n]\),求出 \(k\) 对匹配的最大边权和(不存在则输出 \(-1\))。
\(n\le2\times 10^5\)。
对着别人的代码瞪了整整一天加一下午。
(其实就是刚刚那道板子题的树上版本对吧。)
首先有 \(\text{dp}\) 状态:\(f_{x,i,0/1}\) 表示 \(x\) 子树内,\(i\) 对匹配,\(x\) 选/没选的最大价值。
转移显然(\(v_x\) 表示 \(x\) 节点与父亲的边的边权):
闵可夫斯基和要求必须 \(f\) 关于 \(i\) 有凸性,我们看这个匹配,显然能建出费用流模型。
但是强定必须选 \(i\) 就不是那么美好了,所以我们将 \(f_{x,i,1}\) 的定义改为可选可不选。
(也就是每次 \(f_{x,i,1}\gets f_{x,i,0}\)。)
那既然 \(f\) 是凸的那就很舒服了,我们合并两个子树的复杂度直接从 \(\Theta(|y_1||y_2|)\) 变成了 \(\Theta(|y_1|+|y_2|)\)。
然后你满心欢喜地去看复杂度,发现 \(\Theta(n^2)\to \Theta(n^2)\)。
所以说树形背包真的是个很神奇的东西。
那优化点到底在哪里呢。
其实答案在上面那道例题里,那个错误的方法每次一个点从上一个点转移过来,这次一个点从自己的儿子转移过来,是不是很像。
即使儿子可以快速合并,也会被很长的链卡掉,这启示我们要轻重链剖分。
做到这么大的优化,理论复杂度上界肯定是不可能不变的,我们直接介绍一种在 树上计数背包分治NTT 中广泛应用的算法。
这类算法可以解决一类通用问题,我们都知道,如果合并集合的复杂度是 \(\min(|x|,|y|)\) 的话,利用 dsu on tree 可以轻松做到 \(\Theta(n\log n)\)。
但是如果合并的复杂度是 \(|x|+|y|\) 的话,表面上看数量级没有变化,但是我们却不能轻易优化复杂度。
这种做法可以在 \(\Theta(n\log^2 n)\) 的复杂度内完成上述问题,缺憾是只能求出每个重链链顶的答案,也就是你只能对 \(\Theta(1)\) 个 \(x\) 求 \(f_{x,k}\)。
来说算法流程:
- 首先轻重链剖分。
- 每个点直接把所有轻儿子暴力合并(利用上面提到的分治合并),由于每个点向上至多只有 \(\Theta(\log n)\) 条轻边,每个点这个大小为 \(\Theta(siz_x)\) 的凸包最多会被合并 \(\Theta(\log n)\) 次,每次分治的时候会被访问 \(\Theta(\log n)\) 次,这部分总复杂度 \(\Theta(n\log^2n)\)。
- 重链部分,在链顶处把整条重链使用分治的方法并起来,每个点会在向上的 \(\Theta(\log n)\) 个重链顶被合并,复杂度分析同上。
这种方法看上去比 dsu on tree 复杂度弱了许多,但其优势是能处理本题 \(\text{dp}\) 这种既有复杂的合并操作,合并还会导致数组大小增加的问题。
不要忘了这道题的背后是难以优化的 \((\min,+)\) 卷积。
详细地说合并过程,类似于上题,我们将轻儿子缩到自己身上,这样我们只需要处理重链的分治合并。
你发现我们现在在做类似上题的区间合并,那我们就要同时关注两个端点。
所以我们需要关心上端是否强制不选,下端是否强制不选,设 \(f_{0/1,0/1}\) 是该状态,则转移就是 \(f_{a,b}\cup f_{c,d}\to f_{a,d}\),\(b=c=0\) 的时候就可以把中间的一条边加上。
但这会有个问题:当上下端是同一个点(即分治区间大小为 \(1\))的时候,我们并不能正常完成 \(f_{0,0}+f_{0,0}+w\to f_{0,0}\) 类似的过程,原因显然。
很多代码在这里做了大量的讨论,很丑。
但事实上这部分可以通过一个小技巧规避掉:直接令 \(f_{0,0}\) 在单点时无意义即可,手动模拟一下发现全都吻合,很舒服。
于是你可以免去繁杂的讨论。
但是你发现你的两个大数组合并的时候仍然需要中间那一条边的边权,有没有什么更简洁的方法呢?
你其实可以稍微更改状态,将状态更改为 \(f_{0/1,0/1}\) 表示上端/下端是否一定跟父亲/儿子匹配,同时我们在上端处记录边权,若上端跟父亲匹配,那就将边加到 \(\text{dp}\) 数组中。
重点的是,这个操作并不会改变凸性,因为你现在正在合并一条链,你只需将被钦定的左右两端删掉即可还原回原来的状态。
那么我们的合并也需要做出相应的更改:\(f_{a,b}\cup f_{b,c}\to f_{a,c}\),只有中间的两个点情投意合才能合并,一下子有了一点矩阵乘法的味道。
那我们直接令 \(f_{1,1}=-\infty\),一个点显然不能同时跟父亲儿子匹配。
这样我们就可以大大简化转移,甚至将两个转移的分治合并写到一起。
给一份参考代码,调了好久。
这份代码中的语法特点有很多,不过无关重点。
做这类题最初会有一些不适应,主要是因为我们的思维定式是思考数之间的转换,而对这种数组的转来转去比较陌生。
本题的最优复杂度其实可以做到 \(\Theta(n\log n)\),只需要在每次分治的时候按权找到带权中点即可。
下面是关于复杂度的分析:
我们可以证明该题复杂度是 \(\Theta(n\log n)\) 的。
具体方式只需证明每个凸包被常数次合并之后大小至少变大若干倍即可。
重链部分的复杂度分析类似于全局平衡二叉树,考虑把重链拍成序列,每个点代表的轻子树大小和一定不会超过该点前的前缀和与该点后的后缀和,所以假设左边仍然比右边小太多,没有达到 \(1:2\) 的比例,那左边从右边薅一个点最多薅走右边总大小的一半,也就是将中部的一个点扔到左边之后比例不会超过 \(2:1\),也就是说每个凸包被合并之后 \(siz'>1.5siz\),重链部分证明为 \(\Theta(n\log_{1.5}n)\)。
轻链部分的合并儿子看似不能分析,但合并儿子最大的好处就是没有顺序,那我们类似合并果子,每次把最小的两个合起来,如果被合并的两个凸包 \(A,B\) 较大的那个 \(B\) 本次合并 \(siz\) 没有翻倍,那下次 \(A+B\) 跟另一个凸包 \(C\) 合并的时候一定满足 \(siz_C\ge siz_B\),也就是本次合并后 \(B\) 的 \(siz\) 一定翻倍,每两次合并凸包大小至少翻倍,合并轻儿子部分证明为 \(\Theta(n\log_{\sqrt 2}n)\)。
所以整体的复杂度是 \(\Theta(n\log n)\) 的。
题外话:与矩阵的联系
其实这并不是一个大的部分,但通常在做类似于上面的树上凸包合并时我们要做的并不是朴素的对一个凸包合并,而是多个凸包间的若干复杂关系,当凸包实在过多时,不妨试试矩阵来理顺凸包间的关系。
Gym102331H Honorable Mention
给定一个序列,多组询问 \((l_i,r_i,k_i)\),求 \([l_i,r_i]\) 中选 \(k_i\) 个不交的非空子区间的最大权值和。
\(n\le 3.5\times 10^4,5\text{ seconds}\)。
加上了多组询问那我们就考虑一点常用的数据结构套路。
首先可以使用第一个例题的方式,并保留下分治过程中的凸包矩阵(每个状态都要用到 \(4\) 个凸包)。
然后对于一个区间询问我们会拆成 \(\Theta(\log n)\) 个区间,相当于我们要求出这些区间的凸包矩阵的合并的第 \(k\) 项。
换成普通的背包肯定没辙,但我们保证答案和过程都是凸的。
换位思考一下其实相当于把 \(\Theta(\log n)\) 个有序差分数组归并起来,然后求第 \(k\) 项的值。
那我们直接二分第 \(k\) 项的差分,把所有差分数组在这个值前面的长度找出来相加,看跟 \(k\) 的大小关系即可。
有一个思维误区是可能你觉得求的是矩阵合并而不是朴素的凸包合并就没办法直接做上面的操作了,但实际我们只需要把求出的值组成一个矩阵然后仿照之前的方式合并即可。
也就是说即使合并过程中的状态变化导致凸包左移右移都不要紧,我们的答案是凸的,那我们直接做这个事情就好。
但我们的合并带来了一个问题,你在原来每个凸包用斜率为 \(k\) 的斜线去切然后直接合并那确实是答案,但是经过了矩阵合并的一点点下标偏移之后却并不一定是我们想要的极值了。
但你看我们在做的事情像什么,这不就是个带权二分吗。
所以我们在合并中比较大小的时候需要加上带权二分的系数,以确保我们求出了真正的顶点。
代码。
参考资料
献给 2023 年的自己。
课后习题
之后补充的部分就写在这里吧。
Beautiful World
两个人选装备,每个人都有长为 \(n\) 的装备槽,有 \(m\) 件装备,每件装备最终只能给一个人,每个装备槽也只能放一件装备,第 \(i\) 件装备可以给第一个人的 \(a_i\) 装备槽产生 \(x_i\) 的攻击力加成,或者给第二个人的 \(b_i\) 装备槽产生 \(y_i\) 的攻击力加成,保证存在一种方式使得所有装备都被分完,你需要分配所有装备,最终的总价值为两个人攻击力乘积,使得这个价值最小。
\(n\le 5\times10^5\)。
首先把 \(a_i\) 和 \(b_i+n\) 连边,则这是一个树和基环树并存的图。
基环树中树边显然只能选靠下的点,环边可以有两种选择,总共产生两种方案。
而树相当于选一个点当树根,每条边都选下面那个点,这样大小为 \(o\) 的树就产生了 \(o\) 种可能的情况。
现在的问题是我们有 \(k\) 组向量 \((a_i,b_i)\),你需要每组选一个向量满足最后加起来的横纵坐标乘积最大。
不难发现只有凸包上的点有用,而这又是对向量做 \((\min,+)\) 卷积,直接套上闵可夫斯基和即可。
注意这里的闵可夫斯基和是针对于向量而言的,要使用计算几何写法。
口胡题
给定若干定义域为 \([0,+\infty)\) 的下凸函数(给出构造方法或表达式),选出若干 \(x\) 使得 \(\sum x=m\),且 \(\sum f(x)\) 最小。
Case1:\(x\) 必须是整数,\(m\le 10^6\)。
Case2:\(x\) 可以是实数,\(m\le 10^{18}\)。
Case1 是比较简单的情况,你发现你直接把每个 \(f(x+1)-f(x)\) 扔进堆里,重复 \(m\) 次每次取该权值最小的并把 \(x\gets x+1\)。
Case2:你观察上面这个做法,发现我们其实就是在做 wqs 二分(总答案是若干个凸包的卷积,同样具有凸性),所以直接二分一个 \(k\),对于每个函数求出其导数 \(= k\) 的那一点,求出 \(\sum x\) 并与 \(m\) 做比较即可。


