图计数矩阵树

图论和线性代数的边界之处。

全文约 1.5 万字。

高斯消元求行列式
$\text{LGV}$ 引理
矩阵树定理
$\text{BEST}$ 定理

高斯消元求行列式

ll gau() {ll res=1;
    F(i,1,n) {
        F(j,i+1,n) {
            while(a[i][i]) {
                int d=a[j][i]/a[i][i];
                F(k,i,n) (a[j][k]+=p-d*a[i][k]%p)%=p;
                swap(a[i],a[j]);res=p-res;
            } swap(a[i],a[j]);res=p-res;
        }
    } F(i,1,n) res=res*a[i][i]%p;
    return res;
}

先消成上三角矩阵，再把主对角线上的元素相乘。

每交换一次都需要取反。

LGV 引理

来一个引子：给定一张 $n\times m$ 的网格图，两个点从左下角出发，要到右上角，每次可以向右或向上走一步，且两个人的路径不能在起点终点之外的位置相交，求方案数。

由于不相交，所以可以看作一个人从 $(2,1)$ 走到 $(m,n-1)$，另一个人从 $(1,2)$ 走到 $(m-1,n)$。

有一种优秀的解法：设 $D(n,m)=\binom{n+m}{n}$ 是一个人向右走 $m$ 步，向上走 $n$ 步的方案数，则答案为：

\[D((m-1,n)-(1,2))D((m,n-1)-(2,1))-D((m-1,n)-(2,1))D((m,n-1)-(1,2)) \]

（$(a,b)-(c,d)=(a-c,b-d)$）

用语言描述的话就是分别求出独立走到终点的方案数，然后相乘，交换终点，再求一遍，并减去这次的乘积。

为什么这样是对的？

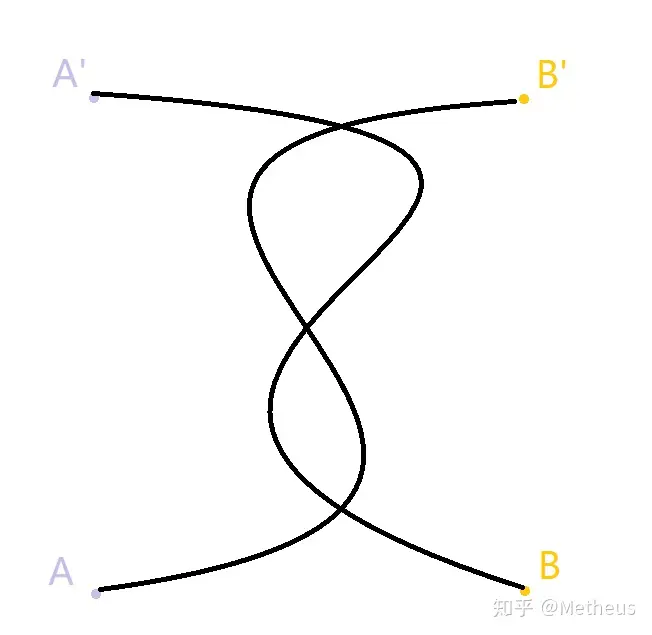
考虑这两个人的路径会发生若干次碰撞，前一种求出的是碰撞了偶数次的方案，后一种求出的是碰撞了奇数次的方案，根据容斥原理除了答案外的每个偶数方案交换终点都可以变成一个奇数方案，所以正确性可证。

用 $e(u,v)$ 表示 $u$ 到 $v$ 的路径条数，则我们的答案可以表示为 $e(A,A')e(B,B')-e(A,B')e(B,A')$。

这个形式有点像一个东西：

\[\begin{vmatrix}e(A,A')&e(A,B)\\e(B,A')&e(B,B')\end{vmatrix} \]

是不是感觉到这背后有一个大坑？

在有向无环图上，给定起点集合 $A$ 与终点集合 $B$，满足 $|A|=|B|=r$。

记一条 $u$ 到 $v$ 的路径为 $u\to v$，记 $\omega(u\to v)$ 为该路径上的边权的积，暂时我们认为边权都为 $1$，定义 $e(u,v)=\sum_{P:u\to v}\omega(P)$，即路径条数。

\[M = \begin{bmatrix}e(A_1,B_1)&e(A_1,B_2)&\cdots&e(A_1,B_r)\\e(A_2,B_1)&e(A_2,B_2)&\cdots&e(A_2,B_r)\\\vdots&\vdots&\ddots&\vdots\\e(A_r,B_1)&e(A_r,B_2)&\cdots&e(A_r,B_r)\end{bmatrix} \]

记不相交方案 $S(\sigma)$：$S(\sigma)_i:A_i\to B_{\sigma_i}$，$\sigma$ 是 $[1,r]$ 的一个排列，$\forall i\ne j$，$S(\sigma)_i$ 和 $S(\sigma)_j$ 没有公共顶点。

$\text{LGV}$ 引理告诉我们，$\det M$ 就是 $A\to B$ 所有不相交路径在所有排列上的带符号和（就是我们通常理解的方案数）。

用容斥原理写成符号形式：

\[\det(M)=\sum_{\sigma}\sum\limits_{S(\sigma)}(-1)^{t(\sigma)}\prod\limits_{i=1}^n \omega(S(\sigma)_i) \]

（$t(S)$ 表示 $S$ 的逆序对数，逆序对是几表示交换了几次终点。）

证明（在通常应用中，我们一般把边权视为 $1$，所以所有的 $\omega$ 都可以视为 $1$，其实使用边权乘积就可以方便处理两点间没有边的情况）：

\[\begin{aligned}\det(M)&=\sum_{\sigma}(-1)^{t(\sigma)}\prod_{i=1}^n e(A_i,B_{\sigma_i})\\&=\sum_{\sigma}(-1)^{t(\sigma)}\prod_{i=1}^n \sum_{P:A_i\to B_{\sigma_i}} \omega(P)\end{aligned} \]

$\prod_{i=1}^n \sum_{P:A_i\to B_{\sigma_i}} \omega(P)$ 实际上是 $A\to B$ 的排列为 $\sigma$ 的任意路径组（即不管是否相交，记为 $R(\sigma)$）的 $\prod_{i=1}^r\omega(R(\sigma)_i)$ 的和。

\[\begin{aligned}&\sum_{\sigma}(-1)^{t(\sigma)}\prod_{i=1}^n \sum_{P:A_i\to B_{\sigma_i}} \omega(P)\\=&\sum_{\sigma}(-1)^{t(\sigma)}\sum_{R(\sigma)}\prod_{i}\omega(R(\sigma)_i)\\=&\sum_{R(\sigma)}(-1)^{t(\sigma)}\prod_i\omega(R(\sigma)_i)\end{aligned} \]

将任意路径组 $R(\sigma)$ 拆成不相交路径组 $U(\sigma)$ 和相交路径组 $V(\sigma)$：

\[\begin{aligned}&\sum_{R(\sigma)}(-1)^{t(\sigma)}\prod_i\omega(R(\sigma)_i)\\=&\sum_{U(\sigma)}(-1)^{t(\sigma)}\prod_i\omega(U(\sigma)_i)+\sum_{V(\sigma)}(-1)^{t(\sigma)}\prod_i\omega(V(\sigma)_i)\end{aligned} \]

其中前一部分是我们的答案，后一部分由于每存在一条 $A_i\to u\to B_{\sigma_i},A_j\to u\to B_{\sigma_j}$，则交换二者终点，其它均不变就可以构造出一个逆序对奇偶性不同，数值相等的结果，二者相互抵消。

那么这玩意有啥用呢。

我们打暴力就像暴力求这个行列式，是阶乘级别的，不过现在我们只需要用低于 $\Theta(n^3)$ 以内的复杂度解决 $e(u,v)$，我们就可以 $\Theta(n^3)$ 求出答案。

CF348D Turtles

上面那个问题，但有些位置有障碍，不能走障碍。

$n,m\le 3000$。

运用 $\text{LGV}$ 引理，我们只需求到一个点的方案数。

这就是另一个经典问题了，将终点视为障碍，设 $f_i$ 是到达第 $i$ 个障碍的方案数，则 $f_i=\sum_jf_jD(x_i-x_j,y_i-y_j)$，按网格顺序转移即可保证拓扑序。

但你枚举上一个障碍总复杂度是 $\Theta(n^2m^2)$ 的。

考虑优化，我们能不能用类似二维前缀和的优化？

其实我们就是要求 $f_{r,c}=\sum_{i=1}^r\sum_{j=1}^c D(r-i,j-c)f_{i,j}$

\[\begin{aligned}f_{r,c}&=\sum_{i=1}^r\sum_{j=1}^c D(r-i,c-j)f_{i,j}\\&=\sum_{i=1}^r\sum_{j=1}^c\frac{(r-i+c-j)!}{(r-i)!(c-j)!}f_{i,j}\end{aligned} \]
是的，然后你就不会拆了。

上述思路对于 $n,m\le 10^7,k\le 5\times 10^3$ 是很好用的，也是很经典的，但是我们在这里使用该方法就像玩原神玩的。

$f_{i,j}=f_{i-1,j}+f_{i-1,j-1},f_{\#}=0$。

代码。

P6657 【模板】LGV 引理 & hdu5852 Intersection is not allowed!

有一个 $n\times n$ 的棋盘，左下角为 $(1,1)$，右上角为 $(n,n)$，若一个棋子在点 $(x,y)$，那么走一步只能走到 $(x+1,y)$ 或 $(x,y+1)$。

现在有 $m$ 个棋子，第 $i$ 个棋子一开始放在 $(a_i,1)$，最终要走到 $(b_i,n)$。问有多少种方案，使得每个棋子都能从起点走到终点，且对于所有棋子，走过路径上的点互不相交。输出方案数 $\bmod\ 998244353$ 的值。

两种方案不同当且仅当存在至少一个棋子所经过的点不同。

$2\leq n\leq10^6$，$1\leq m\leq100$，$1\leq a_1\leq a_2\leq \dots\leq a_m\leq n$，$1\leq b_1\leq b_2\leq \dots\leq b_m\leq n$。

观察这个条件 $a_i\le a_{i+1},b_i\le b_{i+1}$，所以任意合法路径组一定满足 $a_i\to b_i$，所以直接套用模板即可。

Monotonic Matrix

求满足以下条件的 $n\times m$ 矩形的个数：

$A_{i,j}\in\{0,1,2\}$。

$A_{i,j}\le A_{i,j+1}$。

$A_{i,j}\le A_{i+1,j}$。

$n,m\le 3000$。

将坐标视为行列，你发现最后的两条分界线等价于从右上往左下走的两条不相交路径，于是就做完了。

你可能需要讨论 $\{0,1,2\},\{0,2\},\{0,1\},\{1,2\}$，有点麻烦。

你发现可重合但有偏序的路径可以将其中一条平移一个单位，于是就变成了真正意义上的不相交路径。

网格

给定 $n\times m$ 的网格图，网格中有 $C$ 个格子是特殊点，现在要找两条从 $(1,1)$ 到 $(n,m)$ 的路径，要求两条路径经过的特殊点个数之和不能超过 $D$ ，并且两条路径不能在除起点与终点之外格子相交，求路径数。

$n,m\le 10^5,D\le C\le 200$。

首先套一步 $\text{LGV}$，把两条路径变成一条路径，但在最后需要枚举第一条用了多少个特殊点第二条用了多少个。

我们只需要求出 $f_i$ 表示恰好经过了 $i$ 个特殊点的路径方案数就可以了。

这里我产生过疑问，显然最后往答案里加的应该是 $\sum_i\sum_j[i+j\le D](f_ig_j-h_is_j)$ 这种形式，但 $f_ig_j-h_is_j$ 这种东西真的有意义吗，或者说，多了对路径的合法性限制，$\text{LGV}$ 引理的前提在有向无环图上自由行走就不存在了，其证明过程中用到的交换终点后的限制也不同，

但事实上你不应该理解为 $\sum_i\sum_j[i+j\le D](f_ig_j-h_is_j)$，这的确是一种错误理解，你实际上应该理解为 $\sum_i\sum_j[i+j\le D](f_ig_j)-\sum_i\sum_j[i+j\le D](h_is_j)$，这样使用交换终点后路径仍合法的事实就可以获知结论的正确性了。

如何求 $f$？

考虑递推，设 $f_{i,j}$ 为第 $i$ 个点必选，已经选了 $j$ 个点的方案数，转移需要用到不经过中间的特殊点，所以设 $g_{i,j}$ 为从 $i$ 出发，不经过其他特殊点到特殊点 $j$ 的方案数，这个可以经典容斥求出。

Gym102978A Ascending Matrix

求满足以下条件的 $n\times m$ 矩形的个数：

$A_{i,j}\in\mathbb N\cap[1,k]$。

$A_{i,j}\le A_{i,j+1}$。

$A_{i,j}\le A_{i+1,j}$。

$A_{r,c}=v$

$n,m,r,c\le 200,k,v\le 100$。

（建议先往下看到矩阵树中的例题再回来做。）

应用上面那个题的思路，我们首先会处理没有 $A_{r,c}$ 限制的题目。

将坐标视为行列，我们考虑把所有 $(r,c)$ 左下方的路径权值设为 $x$，右上方的路径权值视为 $1$。

跑一遍 $\text{LGV}$ 引理，我们取出 $[x^{v-1}]\det(M)$ 就是答案。

至于怎么求 $\det(M)$，可以去翻看下面的特征多项式，或者直接多项式插值 $\Theta(n^4)$。

矩阵树定理

第一次看见可能是两年以前？

一直觉得这是一个很偏门很朴素的理论，后来发现 $\text{OI}$ 中没有真正的简单理论，任何一个简单的东西都能复杂到难以想象。

注意矩阵树的图中要求不存在自环（其实不注意到这个也可以，自环的影响会抵消）。

记号声明

对于有向图：

\[\begin{aligned}D^{\text{in/out}}_{i,i}&=\deg^{\text{in/out}}_i\\A_{i,j}&=\#e(i,j)\\L^{\text{in/out}}&=D^{\text{in/out}}-A\end{aligned} \]

对于无向图：

\[\begin{aligned}D_{i,i}&=\deg_i\\A_{i,j}&=\#e(i,j)\\L&=D-A\end{aligned} \]

对于一个图来说，$D$ 叫做度数矩阵（入度矩阵出度矩阵），$\#e(i,j)$ 表示 $i$ 连向 $j$ 的边数，$A$ 叫做邻接矩阵，$L$ 叫做图的（出/入度）拉普拉斯矩阵（$\text{Laplacian matrix}$）。

可以看出此处无向图等价于每条无向边转化成两条有向边的有向图，故以下主要讨论有向图情况。

定理叙述

对于无向图，其生成树个数 $t$ 为：

\[t = \det L\binom{1,2,\cdots,i-1,i+1,\cdots,n}{1,2,\cdots,i-1,i+1,\cdots,n} \]

上式对于任意 $i$ 成立。

其中 $L\binom{1,2,\cdots,i-1,i+1,\cdots,n}{1,2,\cdots,i-1,i+1,\cdots,n}$ 表示 $L$ 删去第 $i$ 行第 $i$ 列剩余部分组成的矩阵。

从这里我们可以看出对于任意无向连通图，$\text{rank}(L)=n-1$，且 $n-1$ 阶主子式全部相等。

对于有向图，以 $i$ 为根的内向生成树个数 $t^{\text{in}(i)}$ 为：

\[t^{\text{in}(i)}=\det L^{\text{out}}(G)\binom{1,2,\cdots,i-1,i+1,\cdots,n}{1,2,\cdots,i-1,i+1,\cdots,n} \]

类似的，以 $i$ 为根的外向生成树个数 $t^{\text{out}(i)}$ 为：

\[t^{\text{out}(i)}=\det L^{\text{in}}(G)\binom{1,2,\cdots,i-1,i+1,\cdots,n}{1,2,\cdots,i-1,i+1,\cdots,n} \]

注意到内向树用到的是出度，外向树用到的是入度。

证明似乎超出了我的能力范围，且与应用关系不大，先略过吧。

P6178 【模板】Matrix-Tree 定理

真的是纯板子。

P4111 [HEOI2015] 小 Z 的房间

纯板子。

P4336 [SHOI2016] 黑暗前的幻想乡

给出 $n-1$ 个边集，问从每个边集中选一条边构成生成树的方案数。

$n\le17$。

显然有一个朴素的思路是 $f_{S,T}$ 表示生成树已经加到 $S$ 了，已经选了 $T$ 这些边集的边。

直接算状态数是 $\Theta(4^n)$，但我们发现 $|S|=|T|$，去问了一圈发现这个东西还是 $\Theta(4^n)$，比较神秘。

（$\sum_i\binom n i^2=\sum_i\binom n i\binom n{n-i}=\binom{2n} n$。）

那肯定得换思路了，我们考虑容斥。

设 $f_{S}$ 为 $S$ 这些颜色的边不能选，其他颜色任意，生成树的方案数，则答案为 $\sum_S(-1)^{|S|}f_S$，求 $f_S$ 可以矩阵树定理。

这个容斥是十分巧妙的，复杂度 $\Theta(2^nn^3)$。

来一道相似的题：

P3349 [ZJOI2016] 小星星

给定一颗 $n$ 个点的树和一个 $n$ 个点的无向图，问有多少种编号方式，使得将原树重新编号后每条边都在图上出现。

$n\le17$。

朴素的想法要放到树上来考虑：$f_{i,S}$ 表示子树 $i$ 对应的集合是 $S$ 的方案数，合并儿子是子集枚举。

$\Theta(3^nn^2)$。

有一个想法是枚举哪些边失配，其他任意的方案数。

你发现这不是很好做对吧，很明显的，所有边都失配等价于所有边都在补图中出现，这就归约到原问题了。

我们换一种思路，原题的“排列”这个限制很死，我们能不能直接扔了它？

考虑直接扔掉这个限制，$f_{i,j}$ 表示 $i$ 节点编号是 $j$ 的方案数，有重复编号怎么办？

你发现直接枚举总编号数就可以进行容斥了，具体来说，钦定所有节点只能使用 $S$ 中的编号，换种方式来理解就是 $S$ 之外的元素不准选，其他任意的方案数。

喵喵喵。

P3317 [SDOI2014] 重建

给出 $n$ 个点两两之间有边的概率，问恰好图是一棵树的概率，给定的概率不超过两位小数。

$n\le 50$。

考虑一个合法情况是树边必须出现，非树边必须不出现，于是令所有边都不出现，提前把答案乘上 $\prod(1-p)$，将边的权值设为 $\frac{p}{1-p}$ 然后矩阵树定理即可。

虽然这个题数据太菜了，输入 $1$ 可以当作输入了 $1-\epsilon$，硬算也不会炸精度，但这个题是有正经做法的。

特判输入 $1$，这些边必选，若形成环则 puts("0")，否则缩成连通块，这样就不存在 $1$ 了，然后极端情况下 $n-1$ 次乘上 $0.01$ 精度没有太大问题。

P4455 [CQOI2018] 社交网络

外向树计数，很朴素。

AT_jsc2021_g Spanning Tree

给出每条边必须存在，必须不存在，或可选是否存在，求最终图是树的方案数。

$n\le300$。

把必须存在的缩一下点，缩出环就 $0$。

然后把可选是否存在的边在新图上给连一下（有重边需要练出重边）。

然后就做完了。

[ABC253Ex] We Love Forest

对 $k\in[1,n-1]$ 求出每次从 $m$ 条边中任选一条加上，最终无环的概率。

$n\le 14$。

虽然和矩阵树关系不大，但是可以用矩阵树大大简化。

（押韵）

首先转化成求方案数，最后除 $m^i$ 即可。

设 $f_S$ 为 $S$ 是一棵树的方案数，矩阵树可以直接求出来（下文讲如何 $2^n$ 求）。

然后直接把若干个 $f$ 合并即可，合并的时候需要注意避免重复合并，钦定 $\min S\in T\sube S$ 即可。

$2^n$ 求 $f$ 首先有一个朴素的思路是断开每条边断成两棵树，得到：

\[f_{S}\gets \sum_{T\sub S,T\ne\varnothing}f_{T}f_{S\setminus T}e_{T,S\setminus T} \]

但这样会算重，我们仔细观察发现每条边都会计算一遍，所以直接除掉即可：

\[f_{S}\gets \frac{\sum\limits_{T\sub S,T\ne\varnothing}f_{T}f_{S\setminus T}e_{T,S\setminus T}}{|S|-1} \]

使用集合幂级数可以做到 $2^n\text{poly}(n)$。

P2144 [FJOI2007] 轮状病毒

题目很简单但难以概括。

直接打表可以找到一些规律。

但也可以很暴力的化行列式，因为这个行列式长的很有规律。

唯一有用的定理：行列式等于任意一行的值与其对应的代数余子式的和。

余子式：$M_{i,j}=\det\binom{1,2,\cdots,i-1,i+1,\cdots,n-1,n}{1,2,\cdots,j-1,j+1,\cdots,n-1,n}$，代数余子式 $=(-1)^{i+j}M_{i,j}$。

然后我们就可以暴力拆解成可递推形式了。

前面是矩阵树的皮毛，事实上，矩阵树可以求一些比较神奇的东西。

[ABC323G] Inversion of Tree

给定一个排列 $p$，定义一棵树上的「逆序边」为 $u<v\wedge p_u>p_v$，对 $k\in[0,n-1]$ 求出逆序边数量为这些的树的数量。

$n\le 500,4\text{ seconds}$。

特征多项式详解。

将非逆序边构成的 $\text{Laplacian Matrix}$ 视为 $A$，逆序边的 $\text{Laplacian Matrix} $ 视为 $B$，其实就是要求 $\forall k\in[0,n-1],[x^k]|A+xB|$。

（这个逆序边很没意思，可以任意规定每条边是否重要。）

朴素的做法是将 $x$ 赋值为 $0,1,\cdots,n$ 跑矩阵树然后得到一个系数方程，用多项式插值或者高斯消元搞一搞，$\Theta(n^4)$。

考虑到 $|A+xB|$ 长得很像特征多项式，既然那个东西可以 $\Theta(n^3)$ 求，那我们努力往上凑一凑。

我们肯定希望求出 $D=B^{-1}$ 使得 $BD=I$，那么我们就可以求出 $|A+xB|=\frac{|AD+xBD|}{|D|}=\frac{|AD+xI|}{|D|}$。

很不幸的，$B$ 不一定有逆元，典型的例子是整张图一个逆序边也没有。

我们考虑采用如下方法：

同时对 $A,B$ 进行消元，我们不再寻找非空的一行交换过来，而是寻找非空的一列交换过来。
若 $B$ 这一行已经全空（找不到合法列）则将这一整行乘上 $x$（将 $A$ 这一行复制过来，同时 $A$ 清空）然后把前面消个元接着找。
若已经乘过 $n$ 次以上说明答案全为 $0$。

这样只要没有返回 $0$ 那就是消元成功了。

此时就变成了 $|A'+xI|$，将 $A$ 取个反算特征多项式即可。

这也是 $\Theta(n^3)$ 求出 $|A+xB|$ 的通用方法。

代码。

P6624 [省选联考 2020 A 卷] 作业题

\[val(T)=\left(\sum\limits_{i=1}^{n-1} w_{e_i}\right) \times \gcd(w_{e_1},w_{e_2},\dots,w_{e_{n-1}}) \]
给定无向图，设生成树为 $T$，求 $\sum_Tval(T)$。

$n\le 30,w_i\le152501$。

先来把这个难看的 $(\sum_iw_i)\gcd_iw_i$ 反演掉。

\[\begin{aligned}\sum_iw_i\gcd_iw_i&=\sum_iw_i\sum_{k=1}^{W}k[k=\gcd_iw_i]\\&=\sum_iw_i\sum_{k=1}^Wk[\gcd_i\frac{w_i}k=1]\\&=\sum_iw_i\sum_{k=1}^Wk\sum_{d\mid\gcd_i\frac {w_i}k}\mu(d)\\&=\sum_{k=1}^W\sum_{d=1}^{[\frac W k]}k\mu(d)[\forall i,kd\mid w_i]\sum_iw_i\end{aligned} \]

枚举 $T=kd$，则 $\sum_{d\mid T}\frac T d\mu(d)$ 易得，剩余部分其实就是把 $\forall i,T\mid w_i$ 的边加进去跑矩阵树。

但先别急，这个矩阵树可不是一般意义上的求边权乘积的和，怎么求边权和的和？

矩阵树当然不会废到这都求不了，多项式理论造福全人类。

只需要令每条边的边权为 $wx+1$，则“边权乘积”的一次项恰好就是边权和！

现在我们只需要在 $\bmod \ x^2$ 的意义下算多项式加减乘除即可。

（我本来有段时间不大理解多项式除法，常数除 $x$ 竟然能除出来 $x$ 的正幂次，但后来一想多项式求逆保证了 $ff^{-1}=1$，于是放心了。）

\[\begin{aligned}(ax+c)(bx+d)&=(bc+ad)x+cd\\\frac{ax+c}{bx+d}&=\frac{ad-bc}{d^2}x+\frac c d\end{aligned} \]

不会推下面那个柿子只需要解方程 $(ex+f)(bx+d)=1$ 然后求出 $(ax+c)(ex+f)$ 即可。

代码。

注意取模问题。

P5296 [北京省选集训2019] 生成树计数

给定无向完全图，每条边的边权和 $k$，$\text{val}(T)=(\sum_iw_i)^k$，求 $\sum_T\text{val}(T)$。

$n\le 30,k\le30$。

离正解最近的一次。

你考虑朴素的多项式乘法是：

\[[x^k]f(x)g(x)=\sum_{i=0}^k[x^i]f(x)[x^{k-i}]g(x) \]

但这个题想让你用二项式定理：

\[\begin{aligned}[x^k]f(x)g(x)&=\sum_{i=0}^k\binom{k}{i}[x^i]f(x)[x^{k-i}]g(x)\\&=\sum_{i=0}^k\frac{k!}{i!(k-i)!}[x^i]f(x)[x^{k-i}]g(x)\end{aligned} \]

然后你就不会了。

但你发现这个 $k$ 是固定的啊！那不就相当于求：

\[\begin{aligned}[x^k]f(x)g(x)&=\sum_{i=0}^k\frac{1}{i!(k-i)!}[x^i]f(x)[x^{k-i}]g(x)\\&=\sum_{i=0}^k\frac{[x^i]f(x)}{i!}\frac{[x^{k-i}]g(x)}{(k-i)!}\end{aligned} \]

最后再把答案乘上 $k!$，于是我们最开始直接维护一个 $\sum_{i=0}^k \frac{(wx)^i}{i!}$ 就好了。

需要暴力跑多项式加减乘除，复杂度 $\Theta(n^3k^2)$。

代码。

BEST 定理

若 $G$ 是有向欧拉图，则不同欧拉回路总数 $ec$ 是：

\[\forall i,ec=t^{\text{in}(i)}\prod_{v}(\deg_v-\ 1)! \]

欧拉回路按序排列构成的环不同则欧拉回路不同。

此外，从 $i$ 出发的欧拉回路总数 $ec(i)$ 是：

\[ec(i)=t^{\text{in}(i)}\deg_i!\prod_{v\ne i}(\deg_v-\ 1)! \]

由于指定了起点，欧拉回路按序排列构成的序列不同则欧拉回路不同。

证明是没什么用的，不过可以去理解这个定理：

考虑一个合法欧拉回路方案，假设其从 $1$ 出发并回到 $1$，将 $[2,n]$ 这些节点最后一次走的出边拿出来，可以保证一定不会成环，否则再次绕到一个点时没有出边可以走。

$n-1$ 条出边，没有环，所以这就是内向树。

可以证明这是一个充要条件，即反过来说，如果每个点都选一条内向树上的边最后走，那么剩下的边随便走都能形成欧拉回路。

于是剩下的边随便走就是 $\deg_1!\prod_{v\ne 1}(\deg_i-\ 1)!$，注意 $1$ 并不需要排除一条边。

有一些时候，应用 $\text{BEST}$ 定理时不一定要使用矩阵树，而是利用图的某些性质得到树的个数。

如果不对欧拉回路而是对欧拉路径计数怎么办？

考虑在有向图上欧拉路径与欧拉回路不同当且仅当这是一个半欧拉图，即有一个点出度比入度多 $1$ 作为起点，有一个点入度比出度多 $1$ 作为终点，此时我们把终点向起点连一条有向边，则原图的欧拉路径与新图的欧拉回路对偶。

无向图？

别想了，是 NP-Hard。

P5807 【模板】BEST 定理 | Which Dreamed It

给定有向图，求从 $1$ 出发欧拉回路总数。

$T\le 15,n\le 100$。

需要注意，$\text{BEST}$ 定理使用的前提条件是每个点入度等于出度且孤立连通块大小 $=1$。

删掉所有孤立连通块后，我们就可以使用矩阵树，但要注意的是，矩阵树的部分需要把唯一合法连通块搞出来跑。

虽然你可以把 $a_{i,i}=0$ 的地方忽略，但对于辗转相除的矩阵树写法，这么做有时会产生符号问题，所以还是正常跑比较好。

[AGC051D] C4

有一张 $4$ 个点 $4$ 条边的简单无向连通图，点的编号分别为 $1,2,3,4$ ，边分别连接着 $e_1:(1,2),e_2:(2,3),e_3:(3,4),e_4:(4,1) $。

给定 $4$ 个数 $v_1,v_2,v_3,v_4$ 求满足以下条件的路径数量：

从 $1$ 号点出发并到 $1$ 号点结束，且经过第 $i$ 条边 $e_i$ 恰好 $v_i$ 次。

$v_1,v_2,v_3,v_4 \le 5 \times 10^5$。

考虑发掘一下性质。

虽然判断相等条件不同，但题目确实是想让我们求欧拉回路。

设 $8$ 种不同的连边分别有若干种，可以列出 $8$ 个方程，有 $4$ 个是 $c_1+d_1=v_1$ 这种，另外四个是 $c_1-d_1=c_2-d_2$ 这种。

虽然有八个方程，但后四个方程的秩只有 $3$，所以需要枚举一维。

然后你发现这个判等条件让你的阶乘变成了组合数，但那需要知道哪些边在生成树上，所以需要讨论生成树是哪种情况。

ll D(ll n,ll m) {return n>=0&&m>=0?fac[n+m]*inv[n]%p*inv[m]%p:0;}
inline ll sol(ll c1,ll d1,ll c2,ll d2,ll c3,ll d3,ll c4,ll d4) {
    return D(d4,c1)*(!!c4*!!c3*!!c2*D(d1,c2-1)*D(d2,c3-1)%p*D(d3,c4-1)%p+
                     !!d1*!!c4*!!c3*D(d1-1,c2)*D(d2,c3-1)%p*D(d3,c4-1)%p+
                     !!d2*!!d1*!!c4*D(d1-1,c2)*D(d2-1,c3)%p*D(d3,c4-1)%p+
                     !!d3*!!d2*!!d1*D(d1-1,c2)*D(d2-1,c3)%p*D(d3-1,c4)%p)%p;
}