[JLOI2011]飞行路线 不同的算法,不同的悲伤
题目 :BZOJ2763 洛谷P4568 [JLOI2011]飞行路线
一道最短路的题目,想想写个题解也不错(好久没写题解了_(:з」∠)_)
然后这道题中心思路是dijikstra处理最短路,所以没学过的...咳咳
题目描述
Alice和Bob现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在 n 个城市设有业务,设这些城市分别标记为 0 到 n-1 ,一共有 mm 种航线,每种航线连接两个城市,并且航线有一定的价格。
Alice和Bob现在要从一个城市沿着航线到达另一个城市,途中可以进行转机。航空公司对他们这次旅行也推出优惠,他们可以免费在最多 kk 种航线上搭乘飞机。那么Alice和Bob这次出行最少花费多少?
输入输出格式
输入格式:
数据的第一行有三个整数, n,m,k,分别表示城市数,航线数和免费乘坐次数。
第二行有两个整数, s,t ,分别表示他们出行的起点城市编号和终点城市编号。
接下来有m行,每行三个整数, a,b,c ,表示存在一种航线,能从城市 a 到达城市 b ,或从城市 b 到达城市 a ,价格为 c 。
输出格式:
只有一行,包含一个整数,为最少花费。
输入输出样例
输入样例#1:
5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100
输出样例#1:
8
说明
(只需要100%的数据范围就够了)
对于100%的数据:
2 ≤ n ≤ 10000,1 ≤ m ≤ 50000,0 ≤ k ≤ 10 , 0 ≤ s , t < n ,
0 ≤ a,b < n , a ≠ b , 0 ≤ c ≤ 1000
分析
首先,这是一道最短路的题目(废话,题目前面都讲过了),那么最重要的问题就是处理A、B这俩货白搭飞机的次数了。
那么以下是第一种解法:
第一种解法中,对分析中的问题采取的方法就是将白搭飞机的次数k处理进最短路dis数组中去(就是将dis数组多加一维)
代码如下:
//普通思路的dijikstra
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
typedef long long ll;
using namespace std;
const int M=1e4+100;
inline ll read(){
ll x=0,f=1; char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*f;
}
int dis[M][15];
int n,m,k,s,t,pat;
int in[M][15],head[M];
struct Edge{
int to,val,next;
}e[M*5<<1];
inline void add(int u,int v,int w){
++pat; e[pat].to=v; e[pat].val=w; e[pat].next=head[u]; head[u]=pat;
}
struct pos{ //结构体处理节点问题
int id,num;
friend bool operator < (const pos x,const pos y){ //才发现的friend,神奇+震惊
return x.num>y.num;
}
}nd;
inline void SPFA(){ //抱歉这里其实是dijikstra最短路_(:з」∠)_
nd.id=s; nd.num=0;
priority_queue<pos> Q;
Q.push(nd); in[s][0]=1;
while(!Q.empty()){
pos tmp=Q.top();
int u=tmp.id,g=tmp.num;
in[u][g]=0; Q.pop();
if(dis[u][g]>=dis[t][k]) continue;
for(int i=head[u];i;i=e[i].next){
int v=e[i].to,w=e[i].val;
if(dis[v][g]>dis[u][g]+w){ //(几乎)正常的最短路操作
dis[v][g]=dis[u][g]+w;
if(!in[v][g]){
in[v][g]=1;
pos newp; newp.id=v,newp.num=g;
Q.push(newp);
}
}
if(g<k && dis[v][g+1]>dis[u][g]){ //然后考虑是否可以白搭一次飞机(划不划算)
dis[v][g+1]=dis[u][g];
if(!in[v][g+1]){
in[v][g+1]=1;
pos newp; newp.id=v,newp.num=g+1;
Q.push(newp);
}
}
}
}
}
int main(){
n=read(); m=read(); k=read();
s=read(); t=read();
memset(dis ,0x3f, sizeof(dis));
for(int i=1;i<=m;++i){ //朴素的读边方式
int u=read(),v=read(),w=read();
add(u , v , w); add(v , u , w);
}
dis[s][0]=0; SPFA(); //朴素的最短路
printf("%d\n",dis[t][k]); //然后是朴素的输出
return 0; //最后是朴素的结束(请叫我蒟蒻)
}ok,这个程序要过bzoj是妥妥的了(毕竟bzoj算的是总用时),
然而洛谷非常不给面子的T了我两个点QAQ。
于是我就悲愤的只能去优化了…
于是第二种解法该怎么写呢?
第二种算法是消除了白搭飞机对于求最短路的影响(并且码着码着我发现代码还变短了一丢-_-||)。
那么这是何方神算法呢?其实看到消除影响这里机智的你应该就猜到了一点,估计是把点变多了然后拿空间换时间。
(咳咳,然而事实是用这个算法A了之后的所用空间反而小…原因其实就是在dis数组范围变大之后又减少了一维,即k所代表的的那一维。dis的数组大小在乘以k又除以k之后还是没变过,所以这个算法并不是拿空间换时间,仅仅是将点变多了而已)
那么我们应该如何来增加节点呢?这里用了分层的方法。。。
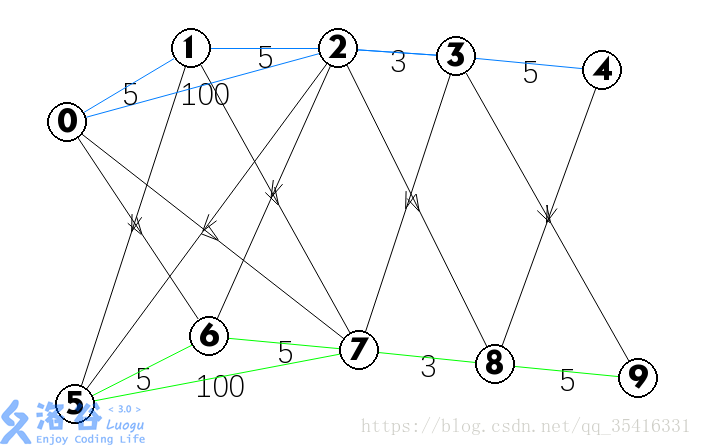
数据的话就用样例,但是怎么用图说话?容我盗个图先:
那么这张图中的5、6、7、8、9五个节点即增加的节点(其实可以看做是上一层节点的“分身”)。
那么这小小的分层图是如何消除白搭飞机这个条件对于最短路求解的影响的呢?就是把原来的图分身出k层,层与层之间的边价值为0,然后再直接SPFA(那么再搞搞事情就是用dijikstra来做),最后直接输出 dis [ t + n * k ] 的值即可(如上图中要输出的dis节点编号为4+5*1=9,即dis[9])。
代码如下:
//分层图做法,效率更高
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
typedef long long ll;
using namespace std;
const int M=1e6+100;
inline ll read(){
ll x=0,f=1; char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*f;
}
int dis[M];
int n,m,k,s,t,pat,top;
int in[M],head[M];
struct Edge{
int to,val,next;
}e[M<<3];
inline void add(int u,int v,int w){
++pat; e[pat].to=v; e[pat].val=w; e[pat].next=head[u]; head[u]=pat;
}
inline bool cmp(int x,int y){
return dis[x]>dis[y];
}
//搞搞堆排序(总觉得不适应STL自定义小根堆)
#define push(x) q[top]=x,++top,push_heap(q,q+top,cmp)
#define pop() pop_heap(q,q+top--,cmp)
inline void SPFA(){ //看这SPFA(dijikstra)多么的短小精悍
int q[M];
push(s); in[s]=1;
while(top){
int u=*q; pop(); in[u]=0;
if(dis[u]>=dis[t]) continue;
for(int i=head[u];i;i=e[i].next){
int v=e[i].to,w=e[i].val;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
if(!in[v]) in[v]=1, push(v);
}
}
}
}
int main(){
n=read(); m=read(); k=read();
s=read(); t=read()+n*k; //读进来的时候终点就直接设成了t+n*k
memset(dis ,0x3f, sizeof(dis));
for(int i=1;i<=m;++i){
int u=read(),v=read(),w=read();
for(int j=0;j<=k;++j){ //存边的时候稍微(几乎没什么压力)累了点
add(u,v,w), add(u,v+n,0);
add(v,u,w), add(v,u+n,0);
u+=n,v+=n;
}
}
dis[s]=0; SPFA(); //然后轻松SPFA(dijikstra)
printf("%d\n",dis[t]); //输出结果
return 0;
}知道为什么我用的M=1e6+吗?╭(╯^╰)╮,因为1e5在洛谷上RE了仨点(难受),于是愤怒之下(当然是在掂量过不会爆内存的情况下)直接把M开成了1e6。
然后下面是效果图(效率提高了…起码10几倍)
Judge课堂再一次over了,bye bye童鞋们!




 浙公网安备 33010602011771号
浙公网安备 33010602011771号