题解 P5270 无论怎样神树大人都会删库跑路

题解 P5270 无论怎样神树大人都会删库跑路

题意已经说得很清楚了，我们直接开始讲题。

首先考虑一次只插入一个字符。问题只在于我们想要判断最后几个字符是否组成相同，即判断两个可重集合是否相等。这个需求很像字符串哈希的目的（快速判断两个字符串是否相等）。但集合怎么哈希呢？

需求一：判断后缀与 \(S\) 是否相等

一个很简单的思路：像做离散化那样把每个字符映射一个随机的值，然后对集合求和来进行判断。

但是同样很显然的，这个做法存在很大缺陷，比如以下映射关系：

原 1 2 3 4 5
映 7 6 8 5 9

这样集合 2 5 和集合 4 4 4 最后哈希出来都是 \(15\)。

但是，我们可以多做几组映射！在所有映射下都相等的集合才判为他俩相等，外加我们的映射是随机给的，因此根本卡不掉。

需求二：一次添加一整个字符串

刚才我们一次只添加了一个字符，但题目要求我们一次添加一整个串。画图来探究一下：

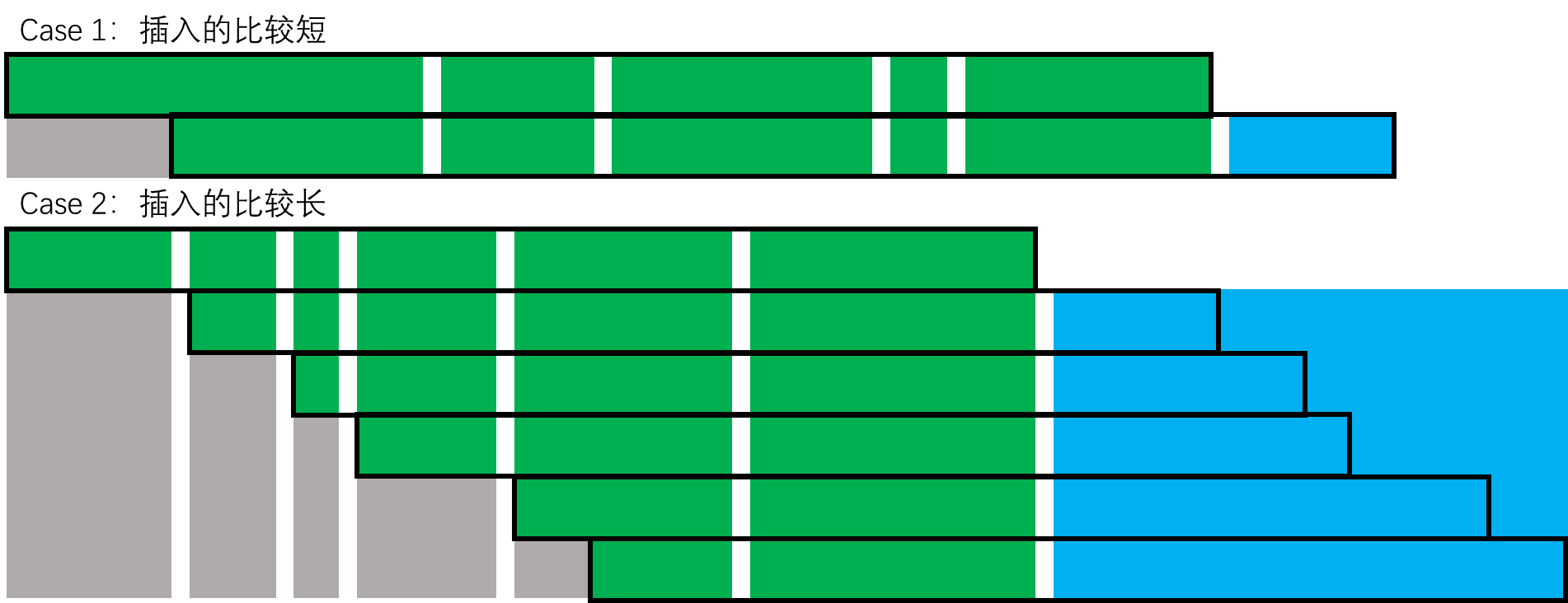
看出点啥来了吗？我们需要预处理每个串内的前缀的哈希值，以及按 \(R\) 数组顺序排列串后的前缀哈希值，就像 Case 2 中插入后第 \(5\) 块绿条并没有完全被踢出范围，于是我们需要先求出最后三条（两绿一蓝）的前缀和，再减去第 \(5\) 条灰色部分的和，这样我们就实现了 \(O(1)\) 进一整个字符串。

需求三：快速地处理循环

但是这题还没有做完。因为 \(Q\le 10^9\)！这喝了 DDV 般的数据范围彻底破灭了我们暴力 hash 的幻想。

仔细分析插入的那个式子：

\[\LARGE a_{R_{((i-1)\bmod m)+1}} \]

看上去挺吓人的，不是吗？但翻译成人话，就是依次插入 \(a_1,a_2,\dots,a_m\)，反复循环直到插入了 \(Q\) 个串。那一个挺好想的思路就是我先暴力的加一遍 \(R\) 数组，然后乘上循环次数，最后单出不到一圈暴力算。

理想很丰满，现实很骨感。这么做是错的，因为刚开始的时候长度还不太够，此时统计出来的答案可能会少，不能用来代表后面的答案。因此我们先手动往里加，一直加到长度达到 \(T\) 了，再按照刚才的思路统计，即可完成本题。

代码