机器学习笔记8

学习内容：
学习决策树、理解信息增益、信息增益率
学习ID3算法优缺点
学习C4.5算法优缺点、理解C4.5算法在ID3算法上有什么提升、学习C4.5算法在连续值上的处理

回答：

（1）学习决策树、理解信息增益、信息增益率

决策树又称为判定树，是运用于分类的一种树结构，其中的每个内部节点代表对某一属性的一次测试，每条边代表一个测试结果，叶节点代表某个类或类的分布。
决策树的决策过程需要从决策树的根节点开始，待测数据与决策树中的特征节点进行比较，并按照比较结果选择选择下一比较分支，直到叶子节点作为最终的决策结果。

有两种树：分类树--对离散变量做决策树，回归树--对连续变量做决策树

决策树的学习过程分为三个部分：

  • 特征选择：从训练数据的特征中选择一个特征作为当前节点的分裂标准（特征选择的标准不同产生了不同的特征决策树算法）。
  • 决策树生成：根据所选特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止声场。
  • 剪枝：决策树容易过拟合，需要剪枝来缩小树的结构和规模（包括预剪枝和后剪枝）。
在决策树算法中,ID3基于信息增益作为属性选择的度量, C4.5基于信息增益作为属性选择的度量, CART基于基尼指数作为属性选择的度量。
信息增益原则对于每个分支节点，都会乘以其权重，也就是说，由于权重之和为1，所以分支节点分的越多，即每个节点数据越小，纯度可能越高。这样会导致信息熵准则偏爱那些取值数目较多的属性。为了解决该问题，这里引入了信息增益率。
信息增益率原则可能对取值数目较少的属性更加偏爱,为了解决这个问题，可以先找出信息增益在平均值以上的属性，在从中选择信息增益率最高的。
（2）学习ID3算法优缺点
ID3算法是由Ross Quinlan提出的决策树的一种算法实现，以信息论为基础，以信息熵和信息增益为衡量标准，从而实现对数据的归纳分类。
ID3算法是建立在奥卡姆剃刀的基础上：越是小型的决策树越优于大的决策树（be simple简单理论）。
ID3算法可用于划分标准称型数据，但存在一些问题：
1）没有剪枝过程，为了去除过渡数据匹配的问题，可通过裁剪合并相邻的无法产生大量信息增益的叶子节点;
2）信息增益的方法偏向选择具有大量值的属性，也就是说某个属性特征索取的不同值越多，那么越有可能作为分裂属性，这样是不合理的；
3）只可以处理离散分布的数据特征
（3）学习C4.5算法优缺点、理解C4.5算法在ID3算法上有什么提升、学习C4.5算法在连续值上的处理
C4.5算法是ID3算法的一种改进。
改进
1）用信息增益率来选择属性，克服了用信息增益选择属性偏向选择多值属性的不足
2）在构造树的过程中进行剪枝
3）对连续属性进行离散化
4）能够对不完整的数据进行处理
对连续值的处理：
将连续型的属性变量进行离散化处理形成决策树的训练集：
1）将需要处理的样本（对应根节点）或样本子集（对应子树）按照连续变量的大小从小到大进行排序
2）假设该属性对应不同的属性值共N个，那么总共有N-1个可能的候选分割值点，每个候选的分割阈值点的值为上述排序后的属性值中两两前后连续元素的中点
3）用信息增益选择最佳划分
代码实现： 
  1 import numpy as np
  2 import pandas as pd
  3 from collections import Counter
  4 from decisionTreePlot import *
  5 
  6 def calcShannonEnt(data):
  7     # print(data.shape[0])
  8     num = data.shape[0]
  9     labelCounts = Counter()
 10     for i in range(num):
 11         labelCounts[data[i][-1]] += 1
 12     # print(labelCounts)
 13     shannonEnt = 0.0
 14     for key in labelCounts:
 15         pro = float(labelCounts[key]) / num
 16         shannonEnt -= pro * np.math.log(pro, 2)
 17     return shannonEnt
 18 
 19 def splitDataSet(data, axis, value):
 20     # print(data)
 21     reDataSet = []
 22     for featVec in data:
 23         # print(featVec)
 24         if featVec[axis] == value:
 25             # print(featVec[axis])
 26             reduceFeatVec = list(featVec[:axis])
 27             reduceFeatVec.extend(featVec[axis+1:])
 28             reDataSet.append(reduceFeatVec)
 29     return np.array(reDataSet)
 30 
 31 def splitContinuousDataSet(data, axis, value, direction):
 32     reDataSet = []
 33     # print(data)
 34     for featVec in data:
 35         # print(featVec)
 36         if direction == 0:
 37             if featVec[axis] > value:
 38                 reduceFeatVec = featVec[:axis]
 39                 reduceFeatVecList = list(reduceFeatVec)
 40                 reduceFeatVecList.extend(featVec[axis+1 :])
 41                 reDataSet.append(reduceFeatVecList)
 42         else:
 43             if featVec[axis] <= value:
 44                 reduceFeatVec = featVec[:axis]
 45                 reduceFeatVecList = list(reduceFeatVec)
 46                 reduceFeatVecList.extend(featVec[axis+1 :])
 47                 reDataSet.append(reduceFeatVecList)
 48     return np.array(reDataSet)
 49 
 50 def chooseBestFeatureToSplit(data):
 51     bestFeature = -1
 52     bestInfoGain = 0.0
 53     baseEntropy = calcShannonEnt(data)
 54     numFeature = data.shape[1] - 1
 55     for i in range(numFeature):
 56         featlist = [example[i] for example in data]
 57         # print(featlist)
 58         if type(featlist[0]).__name__ == 'float' or type(featlist[0]).__name__ == 'int':
 59             sortfeatList = sorted(featlist)
 60             # print(sortfeatList)
 61             splitList = []
 62             for j in range(len(sortfeatList) - 1):
 63                 splitList.append((sortfeatList[j] + sortfeatList[j + 1]) / 2.0)
 64             bestSplitEntropy = 10000
 65             slen = len(splitList)
 66             # print(slen)
 67             for j in range(slen):
 68                 value = splitList[j]
 69                 newEntropy = 0.0
 70                 subDataSet0 = splitContinuousDataSet(data, i, value, 0)
 71                 subDataSet1 = splitContinuousDataSet(data, i, value, 1)
 72 
 73                 pro0 = len(subDataSet0) / len(data)
 74                 newEntropy += pro0 * calcShannonEnt(subDataSet0)
 75                 pro1 = len(subDataSet1) / len(data)
 76                 newEntropy += pro1 * calcShannonEnt(subDataSet1)
 77 
 78                 if newEntropy < bestSplitEntropy:
 79                     bestSplitEntropy = newEntropy
 80                     # bsplit = j
 81                     infoGain = baseEntropy - bestSplitEntropy
 82         else:
 83             uniqueVals = set(featlist)
 84             newEntropy = 0.0
 85             for value in uniqueVals:
 86                 subDataSet = splitDataSet(data, i, value)
 87                 pro = len(subDataSet) / float(len(data))
 88                 newEntropy += pro * calcShannonEnt(subDataSet)
 89             infoGain = baseEntropy - newEntropy
 90         if infoGain > bestInfoGain:
 91             bestInfoGain = infoGain
 92             bestFeature = i
 93     # print(bestInfoGain)
 94     # print(bestFeature)
 95     return bestFeature
 96 
 97 def majorityCnt(classlist):
 98     classCount = {}
 99     for vote in classlist:
100         if vote not in classCount.key():
101             classCount[vote] = 0
102         classCount[vote] += 1
103     return max(classCount)
104 
105 def createTree(dataSet, labels):
106     classList = [example[-1] for example in dataSet]
107     if classList.count(classList[0]) == len(classList):
108         return classList[0]
109     if len(dataSet[0]) == 1:
110         return majorityCnt(classList)
111 
112     bestFeat = chooseBestFeatureToSplit(dataSet)
113     bestFeatLabel = labels[bestFeat]
114     myTree = {bestFeatLabel: {}}
115     del(labels[bestFeat])
116     featValues = [example[bestFeat] for example in dataSet]
117     uniqueVals = set(featValues)
118     for value in uniqueVals:
119         subLabels = labels[:]
120         myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
121     return myTree
122 
123 def test(dataSet, columns):
124     data = np.array([example[1:] for example in dataSet])
125     # print(data)
126     curTree = createTree(data, columns)
127     createPlot(curTree)
128 
129 if __name__ == "__main__":
130     file = pd.read_csv("watermelon_3a.csv")
131     title = file.keys()
132     columns = file.columns.values.tolist()[1:]
133     data = file.values
134     test(data, columns)

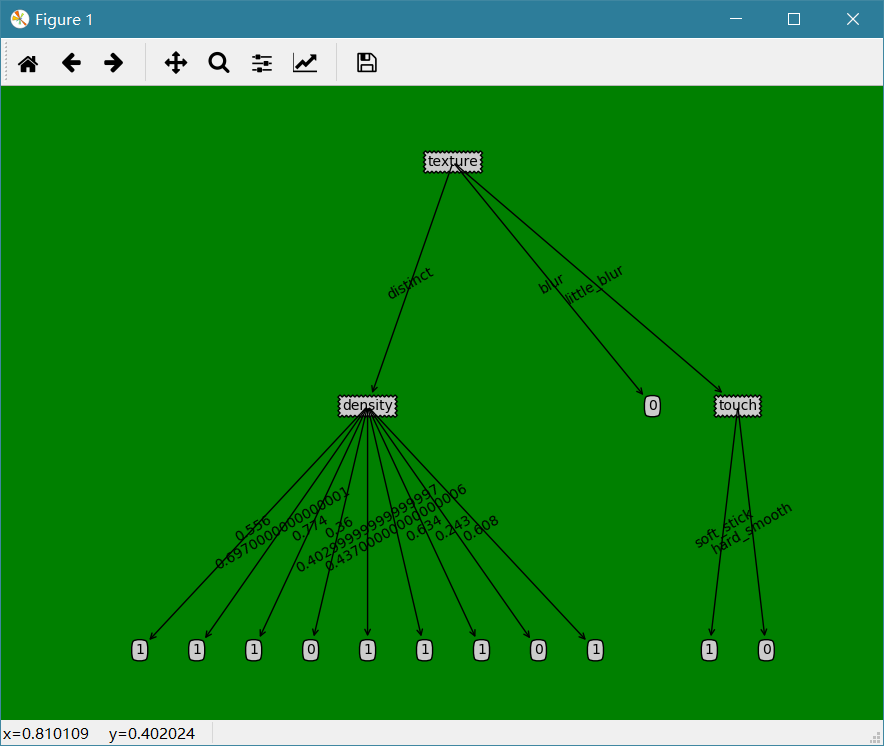
结果展示：

posted @ 2019-06-11 00:36  Joyce_song94  阅读(257)  评论(0)    收藏  举报