二分图建模
二分图简介
二分图是节点由两个集合构成,满足两个集合的内部没有边的图。
给个图理解一下:
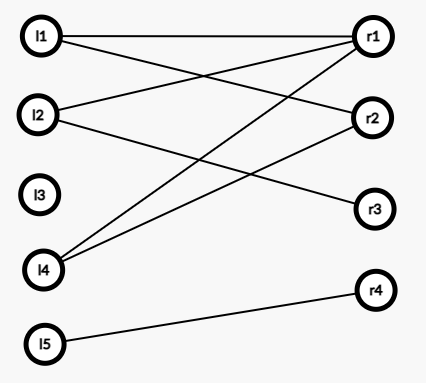
二分图判定
判定方式
很显然,一条边连的两个点一定不属于一个点集,所以我们考虑把图染色:
如果一个点染成黑色,那么与之相邻的点一定会被染成白色。当我们发现一个点相邻的点已经被染过色且与之颜色相同,那么就不是二分图了。反之如果全部满足,那么一定是二分图。
这里我们也得到了二分图的一个重要性质:一定不存在奇环
例题
考虑二分答案。将两人之间矛盾大于等于这个值得连边,然后判断是否为二分图即可。
光明,始于先驱者。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#define N 100005
using namespace std;
int n,m,color[N];
struct edge{
int next,to,dis;
}edge[N << 1];
int head[N << 1],cnt;
void add(int from,int to,int dis){
edge[++cnt].next = head[from];
edge[cnt].to = to;
edge[cnt].dis = dis;
head[from] = cnt;
}
void Input(){
scanf("%d%d",&n,&m);
for(int i = 1,u,v,w;i <= m;i ++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);add(v,u,w);
}
}
queue < int > q;
int check(int mid){
memset(color,0,sizeof(color));
while(!q.empty()) q.pop();
for(int i = 1;i <= n;i ++){
if(!color[i]){
q.push(i);color[i] = 1;
while(!q.empty()){
int x = q.front();q.pop();
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to,w = edge[i].dis;
if(w >= mid){
if(!color[y]){
q.push(y);
if(color[x] == 1) color[y] = 2;
else color[y] = 1;
}
else if(color[y] == color[x]) return 0;
}
}
}
}
}
return 1;
}
void work(){
int l = 0,r = 1e9 + 1;
while(r > l + 1){
int mid = l + r >> 1;
if(check(mid)) r = mid;
else l = mid;
}
printf("%d",l);
return ;
}
int main(){Input();work();return 0;}
二分图建模
转化为最大流模型
令超级源点与左部点、右部点与超级汇点之间以及原左部点向右部点之间存在的边建一条容量为 \(1\) 的边,然后跑最大流即可。
\(1.\) P3386 【模板】二分图最大匹配
无数次,在人世的焦土上,祈望太阳。
#include <iostream>
#include <cstdio>
#include <queue>
#define N 1005
#define M 50004
#define inf 1e18
#define int long long
using namespace std;
int n,m,e,dis[N],now[N];
struct Edge{
int next,to,dis,flow;
}edge[(M + N) << 1];
int head[N],cnt = 1;
void add(int from,int to,int dis){
edge[++cnt] = (Edge){head[from],to,dis,0};
head[from] = cnt;
}
queue < int > q;
int bfs(){
while(!q.empty()) q.pop();q.push(0);
for(int i = 0;i <= n + m + 1;i ++) dis[i] = 0;dis[0] = 1;
while(!q.empty()){
int x = q.front();q.pop();
now[x] = head[x];
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to;
if(!dis[y] and edge[i].flow < edge[i].dis){
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
return dis[n + m + 1];
}
int dfs(int x,int flow){
if(x == n + m + 1 or !flow) return flow;
int res = 0;
for(int i = now[x];i;i = edge[i].next){
now[x] = i;
int y = edge[i].to,d;
if(dis[y] == dis[x] + 1 and (d = dfs(y,min(edge[i].dis - edge[i].flow,flow - res)))){
edge[i].flow += d,edge[i ^ 1].flow -= d;
res += d;if(res == flow) break;
}
}
return res;
}
void Dinic(){
int ans = 0;
while(bfs()) ans += dfs(0,inf);
printf("%lld",ans);
}
void Input(){
scanf("%lld%lld%lld",&n,&m,&e);
for(int i = 1,u,v;i <= e;i ++){
scanf("%lld%lld",&u,&v);
add(u,v + n,1);add(v + n,u,0);
}
for(int i = 1;i <= n;i ++) add(0,i,1),add(i,0,0);
for(int i = 1;i <= m;i ++) add(i + n,n + m + 1,1),add(n + m + 1,i + n,0);
}
signed main(){
Input();
Dinic();
return 0;
}
二分图最小点覆盖(König 定理)
最小点覆盖:选最少的点,满足每条边至少有一个端点被选。
结论:最小点覆盖 \(=\) 最大匹配。证明略。
\(1.\) P7368 [USACO05NOV] Asteroids G
我们对于一个小行星的行和列连一条边。易得如果想打掉一个小行星,要么攻击其所在行,要么攻击其所在列。所以就想到一一个边至少有一个端点被选,转化为了二分图最小点覆盖问题。
光明神已陨落,现在由光明引领我。
#include <bits/stdc++.h>
#define N 1000006
#define inf 1e5
using namespace std;
int n,m,S,T,dis[N];
queue < int > q;
struct Edge{int next,to,dis,flow;}edge[N];
int head[N],now[N],cnt = 1;
void add(int from,int to,int dis){
edge[++cnt] = (Edge){head[from],to,dis,0};
head[from] = cnt;
}
void Input(){
scanf("%d%d",&n,&m);S = 0,T = n * 2 + 1;
for(int i = 1,x,y;i <= m;i ++){
scanf("%d%d",&x,&y);
add(x,y + n,1),add(y + n,x,0);
}
for(int i = 1;i <= n;i ++) add(S,i,1),add(i,S,0);
for(int i = 1;i <= n;i ++) add(i + n,T,1),add(T,i + n,0);
}
bool bfs(){
for(int i = S;i <= T;i ++) dis[i] = 0;
dis[S] = 1,q.push(S);
while(!q.empty()){
int x = q.front();q.pop();
now[x] = head[x];
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to;
if(!dis[y] and edge[i].dis > edge[i].flow){
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
return dis[T];
}
int dfs(int x,int flow){
if(x == T or !flow) return flow;
int res = 0;
for(int i = now[x];i;i = edge[i].next){
now[x] = i;
int y = edge[i].to,d;
if(dis[y] == dis[x] + 1 and (d = dfs(y,min(edge[i].dis - edge[i].flow,flow - res)))){
edge[i].flow += d,edge[i ^ 1].flow -= d;
res += d;if(res == flow) break;
}
}
return res;
}
void work(){
int ans = 0;
while(bfs()) ans += dfs(S,inf);
printf("%d\n",ans);
}
signed main(){Input();work();return 0;}
二分图最大独立集
最大独立集:选最多的点,满足两两之间没有边相连。
结论:最大独立集 \(=n\ -\) 最小点覆盖 \(=n\ -\) 最大匹配。证明略。
一般可用于解决矛盾冲突双方不能同时存在的问题。它一般有两种建图方法:第一种,根据一些性质来确定哪些是左部点,哪些是右部点,然后建图,优点是时间复杂度优。第二种,把一个点拆成两个点,将矛盾的双方分别向对方连边,建图,跑完最大匹配之后除以 \(2\) 即为本来的最大匹配,证明略,优点是好写。
\(1.\) HDU3829 Cat VS Dog
我们将有矛盾的人连边,两个矛盾的人最多只能选一个,所以转化为了最大独立集模型。
另外我们分析是否满足二分图的性质:假设 \(a\) 与 \(b\) 有矛盾,\(b\) 与 \(c\) 有矛盾,那么假设 \(a\) 喜欢猫,那么 \(b\) 一定讨厌猫,\(c\) 就一定喜欢猫,那么 \(a\) 与 \(c\) 之间一定不会有矛盾,因此不存在奇环,所以一定满足建完边之后是一个二分图。
越是没有武器,越要变得强大。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#define N 2003
#define inf 1e5
using namespace std;
int n,m,k,S,T,dis[N],a[N],b[N];
char c[N],d[N];
queue < int > q;
struct Edge{int next,to,dis,flow;}edge[N * N];
int head[N],now[N],cnt = 1;
void add(int from,int to,int dis){
edge[++cnt].next = head[from];
edge[cnt].to = to;
edge[cnt].dis = dis;
edge[cnt].flow = 0;
head[from] = cnt;
}
void Input(){
memset(head,0,sizeof(head));cnt = 1;
S = 0,T = 2 * k + 1;
for(int i = 1;i <= k;i ++) cin >> c[i] >> a[i] >> d[i] >> b[i];
for(int i = 1;i <= k;i ++){
for(int j = 1;j <= k;j ++){
if(c[i] != c[j] && (a[i] == b[j] || a[j] == b[i])){
add(i,j + k,1),add(j + k,i,0);
}
}
}
for(int i = 1;i <= k;i ++) add(S,i,1),add(i,S,0);
for(int i = 1;i <= k;i ++) add(i + k,T,1),add(T,i + k,0);
}
bool bfs(){
for(int i = S;i <= T;i ++) dis[i] = 0;
dis[S] = 1,q.push(S);
while(!q.empty()){
int x = q.front();q.pop();
now[x] = head[x];
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to;
if(!dis[y] && edge[i].dis > edge[i].flow){
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
return dis[T];
}
int dfs(int x,int flow){
if(x == T || !flow) return flow;
int res = 0;
for(int i = now[x];i;i = edge[i].next){
now[x] = i;
int y = edge[i].to,d;
if(dis[y] == dis[x] + 1 && (d = dfs(y,min(edge[i].dis - edge[i].flow,flow - res)))){
edge[i].flow += d,edge[i ^ 1].flow -= d;
res += d;if(res == flow) break;
}
}
return res;
}
void work(){
int ans = 0;
while(bfs()) ans += dfs(S,inf);
printf("%d\n",k - ans / 2);
}
signed main(){while(scanf("%d%d%d",&n,&m,&k) != EOF) Input(),work();return 0;}
\(2.\) P6268 [SHOI2002] 舞会
同样,把跳过舞的人连边,求最大独立集。
同样分析,一个男的和一个女的跳过舞,这个女的可能和另一个男跳过舞,但是这两个男的不会跳过舞,因此一定可以构成二分图。
这是最好的时代,这是最坏的时代,我们一无所有,我们巍然矗立。
#include <bits/stdc++.h>
#define N 2005
#define inf 1e5
using namespace std;
int n,m,S,T,dis[N];
queue < int > q;
struct Edge{int next,to,dis,flow;}edge[N * N];
int head[N],now[N],cnt = 1;
void add(int from,int to,int dis){
edge[++cnt] = (Edge){head[from],to,dis,0};
head[from] = cnt;
}
void Input(){
scanf("%d%d",&n,&m);S = 0,T = 2 * n + 1;
for(int i = 1,a,b;i <= m;i ++){
scanf("%d%d",&a,&b);a ++,b ++;
add(a,b + n,1),add(b + n,a,0);
add(b,a + n,1),add(a + n,b,0);
}
for(int i = 1;i <= n;i ++) add(S,i,1),add(i,S,0);
for(int i = 1;i <= n;i ++) add(i + n,T,1),add(T,i + n,0);
}
bool bfs(){
for(int i = S;i <= T;i ++) dis[i] = 0;
dis[S] = 1,q.push(S);
while(!q.empty()){
int x = q.front();q.pop();
now[x] = head[x];
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to;
if(!dis[y] and edge[i].dis > edge[i].flow){
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
return dis[T];
}
int dfs(int x,int flow){
if(x == T or !flow) return flow;
int res = 0;
for(int i = now[x];i;i = edge[i].next){
now[x] = i;
int y = edge[i].to,d;
if(dis[y] == dis[x] + 1 and (d = dfs(y,min(edge[i].dis - edge[i].flow,flow - res)))){
edge[i].flow += d,edge[i ^ 1].flow -= d;
res += d;if(res == flow) break;
}
}
return res;
}
void work(){
int ans = 0;
while(bfs()) ans += dfs(S,inf);
printf("%d\n",n - ans / 2);
}
signed main(){Input();work();return 0;}
\(3.\) P4304 [TJOI2013] 攻击装置
自己模拟会发现这也满足二分图的性质。
侯非侯,王非王,千乘万骑走北邙。
#include <bits/stdc++.h>
#define N 80005
#define M 2000006
#define inf 1e5
using namespace std;
int n,S,T,dis[N],a[205][205],cnt_a,tot;
char c[205][205];queue < int > q;
int P[8] = {-1,-2,1,2,-1,-2,1,2};
int Q[8] = {-2,-1,-2,-1,2,1,2,1};
struct Edge{int next,to,dis,flow;}edge[M];
int head[N],now[N],cnt = 1;
void add(int from,int to,int dis){
edge[++cnt] = (Edge){head[from],to,dis,0};
head[from] = cnt;
}
void Input(){
scanf("%d",&n);S = 0,T = n * n * 2 + 1;
for(int i = 1;i <= n;i ++){
for(int j = 1;j <= n;j ++){
cin >> c[i][j];
a[i][j] = ++ cnt_a;
if(c[i][j] == '0'){
tot ++;
add(S,a[i][j],1),add(a[i][j],S,0);
add(a[i][j] + n * n,T,1),add(T,n * n + a[i][j],0);
}
}
}
for(int i = 1;i <= n;i ++){
for(int j = 1;j <= n;j ++){
if(c[i][j] == '1') continue;
for(int k = 0;k < 8;k ++){
int x = i + P[k],y = j + Q[k];
if(x > 0 and x <= n and y > 0 and y <= n and c[x][y] == '0'){
add(a[i][j],a[x][y] + cnt_a,1),add(a[x][y] + cnt_a,a[i][j],0);
}
}
}
}
}
bool bfs(){
for(int i = S;i <= T;i ++) dis[i] = 0;
dis[S] = 1;q.push(S);
while(!q.empty()){
int x = q.front();q.pop();
now[x] = head[x];
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to;
if(!dis[y] and edge[i].dis > edge[i].flow){
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
return dis[T];
}
int dfs(int x,int flow){
if(x == T or !flow) return flow;
int res = 0;
for(int i = now[x];i;i = edge[i].next){
now[x] = i;
int y = edge[i].to,d;
if(dis[y] == dis[x] + 1 and (d = dfs(y,min(edge[i].dis - edge[i].flow,flow - res)))){
edge[i].flow += d,edge[i ^ 1].flow -= d;
res += d;if(res == flow) break;
}
}
return res;
}
void work(){
int ans = 0;
while(bfs()) ans += dfs(S,inf);
printf("%d\n",tot - ans / 2);
}
int main(){
Input();work();return 0;
}
\(4.\) P3033 [USACO11NOV] Cow Steeplechase G
同样,横着的只会与竖着的矛盾,因此构成二分图,矛盾的连边,跑最大独立集。
一无所有,至少能肆意如风。
#include <bits/stdc++.h>
#define N 1005
#define inf 1e5
using namespace std;
int n,m,S,T,dis[N];char jilu[N];
struct W{int a,b,c,d;}w[N];
queue < int > q;
struct Edge{int next,to,dis,flow;}edge[N * N];
int head[N],now[N],cnt = 1;
void add(int from,int to,int dis){
edge[++cnt] = (Edge){head[from],to,dis,0};
head[from] = cnt;
}
void Input(){
scanf("%d",&n);S = 0,T = n + 1;
for(int i = 1;i <= n;i ++){
scanf("%d%d%d%d",&w[i].a,&w[i].b,&w[i].c,&w[i].d);
if(w[i].a == w[i].c){
jilu[i] = 'l',add(i,T,1),add(T,i,0);
if(w[i].b > w[i].d) swap(w[i].b,w[i].d);
}
if(w[i].b == w[i].d){
jilu[i] = 'h';add(S,i,1),add(i,S,0);
if(w[i].a > w[i].c) swap(w[i].a,w[i].c);
}
}
for(int i = 1;i <= n;i ++){
if(jilu[i] == 'l') continue;
for(int j = 1;j <= n;j ++){
if(i == j or jilu[j] == 'h') continue;
if(w[i].a <= w[j].a and w[j].a <= w[i].c and w[j].b <= w[i].b and w[i].b <= w[j].d){
add(i,j,1),add(j,i,0);
}
}
}
}
bool bfs(){
for(int i = S;i <= T;i ++) dis[i] = 0;
dis[S] = 1,q.push(S);
while(!q.empty()){
int x = q.front();q.pop();
now[x] = head[x];
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to;
if(!dis[y] and edge[i].dis > edge[i].flow){
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
return dis[T];
}
int dfs(int x,int flow){
if(x == T or !flow) return flow;
int res = 0;
for(int i = now[x];i;i = edge[i].next){
now[x] = i;
int y = edge[i].to,d;
if(dis[y] == dis[x] + 1 and (d = dfs(y,min(edge[i].dis - edge[i].flow,flow - res)))){
edge[i].flow += d,edge[i ^ 1].flow -= d;
res += d;if(res == flow) break;
}
}
return res;
}
void work(){
int ans = 0;
while(bfs()) ans += dfs(S,inf);
printf("%d",n - ans);
}
signed main(){Input(),work();return 0;}
二分图最小边覆盖
选最少的边,满足该图上每一个节点都与这些边中的某一条边关联。
结论:最小边覆盖 \(=n\ -\) 最大匹配。
但存在孤立点的图不存在最小点覆盖。
证明:
为了使边覆盖数最小,肯定会优先选择最大匹配的边,因为它会一次性覆盖两个点并且也不会重复。
假设总边数是 \(n\),最大匹配数是 \(m\),那么剩下点的个数为 \(n-2m\)。
剩下的边已经不存在一个边能覆盖两个没有覆盖的点,因此剩下的边要用 \(n-2m\) 个边来覆盖。
所以最小边覆盖 \(=n-2m+m=n-m\)。
得证。
\(1.\) POJ3020 Antenna Placement
题目大意:最少的用 \(1\times 2\) 的圈(只能水平方向或竖直方向圈)圈住所有 * 的数量。
很明显把可以圈住两个 * 的两个位置连边,然后跑最小边覆盖就行了。
不会让长安城,将我遗忘。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#define N 1005
#define inf 1e5
using namespace std;
int n,m,S,T,dis[N],a[45][45],cnt_a,Q,tot;
char c[45][45];
queue < int > q;
struct Edge{int next,to,dis,flow;}edge[N * N];
int head[N],now[N],cnt = 1;
void add(int from,int to,int dis){
edge[++cnt].next = head[from];
edge[cnt].to = to;
edge[cnt].dis = dis;
edge[cnt].flow = 0;
head[from] = cnt;
}
void Input(){
scanf("%d%d",&n,&m);S = 0,T = n * m * 2 + 1;
memset(head,0,sizeof(head));cnt = 1;cnt_a = tot = 0;
for(int i = 1;i <= n;i ++){
for(int j = 1;j <= m;j ++){
cin >> c[i][j];
a[i][j] = ++ cnt_a;
if(c[i][j] == '*'){
tot ++;
add(S,cnt_a,1),add(cnt_a,S,0);
add(cnt_a + n * m,T,1),add(T,cnt_a + n * m,0);
}
}
}
for(int i = 1;i <= n;i ++){
for(int j = 1;j <= m;j ++){
if(c[i][j] == '*' and j != m){
add(a[i][j],a[i][j + 1] + cnt_a,1),add(a[i][j + 1] + cnt_a,a[i][j],0);
add(a[i][j + 1],a[i][j] + cnt_a,1),add(a[i][j] + cnt_a,a[i][j + 1],0);
}
if(c[i][j] == '*' and i != n){
add(a[i][j],a[i + 1][j] + cnt_a,1),add(a[i + 1][j] + cnt_a,a[i][j],0);
add(a[i + 1][j],a[i][j] + cnt_a,1),add(a[i][j] + cnt_a,a[i + 1][j],0);
}
}
}
}
bool bfs(){
for(int i = S;i <= T;i ++) dis[i] = 0;
dis[S] = 1,q.push(S);
while(!q.empty()){
int x = q.front();q.pop();
now[x] = head[x];
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to;
if(!dis[y] and edge[i].dis > edge[i].flow){
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
return dis[T];
}
int dfs(int x,int flow){
if(x == T or !flow) return flow;
int res = 0;
for(int i = now[x];i;i = edge[i].next){
now[x] = i;
int y = edge[i].to,d;
if(dis[y] == dis[x] + 1 and (d = dfs(y,min(edge[i].dis - edge[i].flow,flow - res)))){
edge[i].flow += d,edge[i ^ 1].flow -= d;
res += d;if(res == flow) break;
}
}
return res;
}
void work(){
int ans = 0;
while(bfs()) ans += dfs(S,inf);
printf("%d\n",tot - ans / 2);
}
signed main(){scanf("%d",&Q);while(Q --) Input(),work();return 0;}
有向无环图的最小不相交路径覆盖
定义:在一个有向图中,找出最少的路径,使得这些路径经过了所有的点,但是要满足每个路径经过的顶点互不相同。
举个例子:
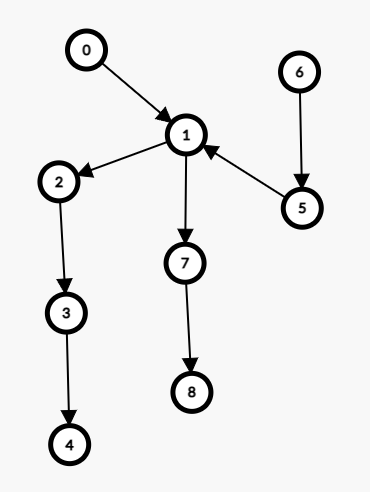
例如这个图,可行的一个最小不相交路径覆盖为 \(0\to1\to2\to3\to4\ ,6\to5\ ,7\to 8\),为 \(3\)。但是不能选择 \(0\to1\to2\to3\to4\ ,6\to5\to1\to7\to 8\),因为有都重复走了 \(1\) 这个点。
把原图的每个店拆点为 \(V_x\ ,V_y\) 两个点,如果有一条有向边 \(A\to B\),那么就加边 \(A_x\to B_y\),这样就得到了一个二分图。
结论:有向无环图的最小不相交路径覆盖 \(=n\ -\) 新图的最大匹配。
证明:
一开始每个点都是独立的为一条路径,总共有n条不相交路径。我们每次在二分图里找一条匹配边就相当于把两条路径合成了一条路径,也就相当于路径数减少了 \(1\)。所以找到了几条匹配边,路径数就减少了多少。所以得证。
\(1.\) POJ1422 Air Raid
有向无环图的最小可相交路径覆盖
定义:在一个有向图中,找出最少的路径,使得这些路径经过了所有的点,但是不需要满足每个路径经过的顶点互不相同。
仍然是这个图:

但是这次可行一种覆盖方法可以是 \(0\to1\to2\to3\to4\ ,6\to5\to1\to7\to8\),因为可以相交。
首先求出原图的 传递闭包,然后就转化为了有向无环图的最小不相交路径覆盖。
证明:其正确性显然
可以感性理解一下,这么做相当于把能连通的边加了一条直接相连的边,你就可以感性理解为 \(5\) 和 \(7\) 之间加了一条边。
\(1.\) POJ2594 Treasure Exploration
我们未知拂晓何方,我们唯有彻夜前行。
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#define N 1005
#define inf 1e5
using namespace std;
int n,m,S,T,dis[N];
bool f[505][505];
queue < int > q;
struct Edge{int next,to,dis,flow;}edge[N * N];
int head[N],now[N],cnt = 1;
void add(int from,int to,int dis){
edge[++cnt].next = head[from];
edge[cnt].to = to;
edge[cnt].dis = dis;
edge[cnt].flow = 0;
head[from] = cnt;
}
void Input(){
S = 0,T = 2 * n + 1;memset(f,0,sizeof(f));
memset(head,0,sizeof(head));cnt = 1;
for(int i = 1,u,v;i <= m;i ++) scanf("%d%d",&u,&v),f[u][v] = 1;
for(int k = 1;k <= n;k ++){
for(int i = 1;i <= n;i ++){
for(int j = 1;j <= n;j ++){
f[i][j] |= f[i][k] & f[k][j];
}
}
}
for(int i = 1;i <= n;i ++){
for(int j = 1;j <= n;j ++){
if(f[i][j]){
add(i,j + n,1),add(j + n,i,0);
}
}
}
for(int i = 1;i <= n;i ++) add(S,i,1),add(i,S,0);
for(int i = 1;i <= n;i ++) add(i + n,T,1),add(T,i + n,0);
}
bool bfs(){
for(int i = S;i <= T;i ++) dis[i] = 0;
dis[S] = 1,q.push(S);
while(!q.empty()){
int x = q.front();q.pop();
now[x] = head[x];
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to;
if(!dis[y] and edge[i].dis > edge[i].flow){
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
return dis[T];
}
int dfs(int x,int flow){
if(x == T or !flow) return flow;
int res = 0;
for(int i = now[x];i;i = edge[i].next){
now[x] = i;
int y = edge[i].to,d;
if(dis[y] == dis[x] + 1 and (d = dfs(y,min(edge[i].dis - edge[i].flow,flow - res)))){
edge[i].flow += d,edge[i ^ 1].flow -= d;
res += d;if(res == flow) break;
}
}
return res;
}
void work(){
int ans = 0;
while(bfs()) ans += dfs(S,inf);
printf("%d\n",n - ans);
}
signed main(){
while(scanf("%d%d",&n,&m)){
if(n == 0 and m == 0) break;
Input(),work();
}
return 0;
}
其它经典题型
\(1.\) P2825 [HEOI2016/TJOI2016] 游戏
注意:可能有些人会想,我能不能像上面求最大独立集一样,把矛盾的连上边,然后求最大独立集。答案是不能的。因为在一行中的三个点 \(a,b,c\),\(a\) 与 \(b\) 有矛盾,\(b\) 与 \(c\) 有矛盾,\(a\) 与 \(c\) 也有矛盾,所以无法构成二分图,因此不能使用最大独立集去做。
所以我们以行和列作为两个点集,我们把一个空地的行和列之间连边,相当于就是求最大匹配,需要尽可能多的让行和列对应。但是由于存在墙,所以我们把一行中两堵墙或者墙与边界之间看成独立的一行,列也同样如此,这样我们就完美的处理了有墙存在的问题。(至于正确性可以自己思考)
投身天地这熔炉,总有些梦想和意志,会因此薪火相传
#include <bits/stdc++.h>
#define N 1000006
#define inf 1e5
using namespace std;
int n,m,S,T,dis[N],cnth,cntl;
char c[55][55];
struct A{int x,y;}b[55][55];
queue < int > q;
struct Edge{int next,to,dis,flow;}edge[N];
int head[N],now[N],cnt = 1;
void add(int from,int to,int dis){
edge[++cnt] = (Edge){head[from],to,dis,0};
head[from] = cnt;
}
void JD(){
for(int i = 1;i <= n;i ++){
cnth ++;
for(int j = 1;j <= m;j ++){
b[i][j].x = cnth;
if(c[i][j] == '#') cnth ++;
}
}
for(int j = 1;j <= m;j ++){
cntl ++;
for(int i = 1;i <= n;i ++){
b[i][j].y = cntl;
if(c[i][j] == '#') cntl ++;
}
}
}
void Input(){
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i ++){
for(int j = 1;j <= m;j ++){
cin >> c[i][j];
}
}
JD();S = 0,T = cnth + cntl + 1;
for(int i = 1;i <= n;i ++){
for(int j = 1;j <= m;j ++){
if(c[i][j] == '*'){
add(b[i][j].x,b[i][j].y + cnth,1);
add(b[i][j].y + cnth,b[i][j].x,0);
}
}
}
for(int i = 1;i <= cnth;i ++) add(S,i,1),add(i,S,0);
for(int i = 1;i <= cntl;i ++) add(i + cnth,T,1),add(T,i + cnth,0);
}
bool bfs(){
for(int i = S;i <= T;i ++) dis[i] = 0;
dis[S] = 1,q.push(S);
while(!q.empty()){
int x = q.front();q.pop();
now[x] = head[x];
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to;
if(!dis[y] and edge[i].dis > edge[i].flow){
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
return dis[T];
}
int dfs(int x,int flow){
if(x == T or !flow) return flow;
int res = 0;
for(int i = now[x];i;i = edge[i].next){
now[x] = i;
int y = edge[i].to,d;
if(dis[y] == dis[x] + 1 and (d = dfs(y,min(edge[i].dis - edge[i].flow,flow - res)))){
edge[i].flow += d,edge[i ^ 1].flow -= d;
res += d;if(res == flow) break;
}
}
return res;
}
void work(){
int ans = 0;
while(bfs()) ans += dfs(S,inf);
printf("%d\n",ans);
}
signed main(){Input();work();return 0;}
\(2.\) P2319 [HNOI2006] 超级英雄
注意此题不是单纯的最大匹配,即我们必须做完第 \(1\) 道题后去做第 \(2\) 道题,做完第 \(2\) 道题后去做第 \(3\) 道题……因此我们的思路是,边加边,边在残留网络上跑,这样可以保证一定是从第一道题依次向后进行的。如果我们发现某一次的最大流不是当前题,那么证明切不到这一题,直接跳出循环即可。
对于输出每个题用的锦囊妙计,我们直接在网络上看哪一个边的当前流量(\(flow\))是 \(1\),证明此边连接的题和锦囊妙计对应,处理答案输出即可。不会实现可以参考代码。
我们的共同点,是都想做第一个看到黎明的人吧。
#include <bits/stdc++.h>
#define N 100005
#define inf 100005
using namespace std;
int n,m,S,T,dis[N],ans,sum,num[N];
queue < int > q;
struct Edge{int next,to,dis,flow;}edge[N];
int head[N],now[N],cnt = 1;
void add(int from,int to,int dis){
edge[++cnt] = (Edge){head[from],to,dis,0};
head[from] = cnt;
}
bool bfs(){
for(int i = S;i <= T;i ++) dis[i] = 0;
dis[S] = 1,q.push(S);
while(!q.empty()){
int x = q.front();q.pop();
now[x] = head[x];
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to;
if(!dis[y] and edge[i].dis > edge[i].flow){
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
return dis[T];
}
int dfs(int x,int flow){
if(x == T or !flow) return flow;
int res = 0;
for(int i = now[x];i;i = edge[i].next){
now[x] = i;
int y = edge[i].to,d;
if(dis[y] == dis[x] + 1 and (d = dfs(y,min(edge[i].dis - edge[i].flow,flow - res)))){
edge[i].flow += d,edge[i ^ 1].flow -= d;
res += d;if(res == flow) break;
}
}
return res;
}
int main(){
scanf("%d%d",&n,&m);sum = m;S = 0,T = n + m + 1;
for(int i = 1;i <= n;i ++) add(S,i,1),add(i,S,0);
for(int i = 1;i <= m;i ++) add(i + n,T,1),add(T,i + n,0);
for(int i = 1,a,b;i <= m;i ++){
scanf("%d%d",&a,&b);a ++,b ++;
add(a,i + n,1),add(i + n,a,0);
add(b,i + n,1),add(i + n,b,0);
while(bfs()) ans += dfs(S,inf);
if(ans != i) {sum = i - 1;break;}
}
printf("%d\n",sum);
for(int i = 1;i <= n;i ++){
for(int j = head[i];j;j = edge[j].next){
int y = edge[j].to;
if(y == S) continue;
if(edge[j].flow == 1){
num[y - n] = i;
break;
}
}
}
for(int i = 1;i <= sum;i ++) printf("%d\n",num[i] - 1);
return 0;
}
\(3.\) P1129 [ZJOI2007] 矩阵游戏
可见只要 \(n\) 行和 \(n\) 列最大匹配是 \(n\) 就行了。因为我们交换两行的本质是交换超级源点 \(S\) 向他们两个的连边,最大匹配不变,交换列同样如此。
身躯于风雪中重塑,心念在绝境中新生。
#include <bits/stdc++.h>
#define N 1005
#define inf 1e5
using namespace std;
int n,m,S,T,dis[N],Q;
queue < int > q;
struct Edge{int next,to,dis,flow;}edge[N * N];
int head[N],now[N],cnt = 1;
void add(int from,int to,int dis){
edge[++cnt] = (Edge){head[from],to,dis,0};
head[from] = cnt;
}
void Input(){
scanf("%d",&n);S = 0,T = 2 * n + 1;
memset(head,0,sizeof(head));cnt = 1;
for(int i = 1;i <= n;i ++){
for(int j = 1,x;j <= n;j ++){
scanf("%d",&x);
if(x == 1) add(i,j + n,1),add(j + n,i,0);
}
}
for(int i = 1;i <= n;i ++) add(S,i,1),add(i,S,0);
for(int i = 1;i <= n;i ++) add(i + n,T,1),add(T,i + n,0);
}
bool bfs(){
for(int i = S;i <= T;i ++) dis[i] = 0;
dis[S] = 1,q.push(S);
while(!q.empty()){
int x = q.front();q.pop();
now[x] = head[x];
for(int i = head[x];i;i = edge[i].next){
int y = edge[i].to;
if(!dis[y] and edge[i].dis > edge[i].flow){
dis[y] = dis[x] + 1;
q.push(y);
}
}
}
return dis[T];
}
int dfs(int x,int flow){
if(x == T or !flow) return flow;
int res = 0;
for(int i = now[x];i;i = edge[i].next){
now[x] = i;
int y = edge[i].to,d;
if(dis[y] == dis[x] + 1 and (d = dfs(y,min(edge[i].dis - edge[i].flow,flow - res)))){
edge[i].flow += d,edge[i ^ 1].flow -= d;
res += d;if(res == flow) break;
}
}
return res;
}
void work(){
int ans = 0;
while(bfs()) ans += dfs(S,inf);
puts(ans == n ? "Yes" : "No");
}
signed main(){scanf("%d",&Q);while(Q --) Input(),work();return 0;}

 一念通天,神魔无惧。如有一味绝境,非历十方生死。雷电遽散。
一念通天,神魔无惧。如有一味绝境,非历十方生死。雷电遽散。

