莫比乌斯函数与莫比乌斯反演
https://www.luogu.com/article/vycu5sds
https://www.cnblogs.com/heyuhhh/p/11231502.html
https://www.luogu.com/article/qkowpfcc
前置
数论分块
简介
数论分块可以快速计算一些含有除法向下取整的和式。它主要运用富比尼定理,将 \(\left\lfloor{\dfrac{n}{i}}\right\rfloor\) 相同的数打包计算。
引理
\(\forall a,b,c\in\mathbb{Z}\),\(\left\lfloor{\dfrac{a}{bc}}\right\rfloor=\left\lfloor{\dfrac{\left\lfloor{\dfrac{a}{b}}\right\rfloor}{c}}\right\rfloor\)。
证明:
\(\dfrac{a}{b}=\left\lfloor{\dfrac{a}{b}}\right\rfloor+r(0\le r<1)\),则 \(\left\lfloor{\dfrac{a}{bc}}\right\rfloor=\left\lfloor{\dfrac{a}{b}\times\dfrac{1}{c}}\right\rfloor=\left\lfloor{\dfrac{1}{c}\times\left(\left\lfloor{\dfrac{a}{b}+r}\right\rfloor\right)}\right\rfloor=\left\lfloor{\dfrac{\left\lfloor{\dfrac{a}{b}}\right\rfloor}{c}+\dfrac{r}{c}}\right\rfloor=\left\lfloor{\dfrac{\left\lfloor{\dfrac{a}{b}}\right\rfloor}{c}}\right\rfloor\)。
形式一
求:\(\begin{aligned}\sum\limits_{i=1}^n\left\lfloor{\dfrac{n}{i}}\right\rfloor\end{aligned}\)。
我们知道有许多 \(\left\lfloor{\dfrac{n}{i}}\right\rfloor\) 的值是一样的,而且它们是呈块状分布的。我们容易得到:对于每一个值相同的块,它的最后一个数是 \(\left\lfloor{\dfrac{n}{\left\lfloor{\dfrac{n}{i}}\right\rfloor}}\right\rfloor\)。
例题:UVA11526
海螺,海诺,唔,这个小海螺你要收好咯,能听到我隐藏版的歌声唷
#include <bits/stdc++.h>
#define int long long
using namespace std;
int T,n;
int H(int x){
int res = 0,l = 1,r;
while(l <= x){
r = x / (x / l);
res += (r - l + 1) * (x / l);
l = r + 1;
}
return res;
}
signed main(){
scanf("%lld",&T);while(T --){
scanf("%lld",&n);
printf("%lld\n",H(n));
}
return 0;
}
形式二
给定 \(k\),求:\(\begin{aligned}\sum\limits_{i=1}^nk\bmod i\end{aligned}\)。
推导:原式 \(\begin{aligned}=\sum\limits_{i=1}^nk-i\times \left\lfloor{\dfrac{k}{i}}\right\rfloor=n\times k-\sum\limits_{i=1}^ni\times \left\lfloor{\dfrac{k}{i}}\right\rfloor\end{aligned}\)。推导毕。
注意处理一下边界的细节问题。
例题 P2261 [CQOI2007] 余数求和
要藏好我的鱼尾巴,别被人类发现啦!
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,k;
int H(){
int res = 0,l = 1,r;
while(l <= min(n,k)){
r = k / (k / l);
if(r > n) res += (l + n) * (n - l + 1) / 2 * (k / l);
else res += (l + r) * (r - l + 1) / 2 * (k / l);
l = r + 1;
}
return res;
}
signed main(){
scanf("%lld%lld",&n,&k);
printf("%lld",n * k - H());
return 0;
}
形式三
求:\(\begin{aligned}\sum\limits_{i=1}^nf(i)\times \left\lfloor{\dfrac{n}{i}}\right\rfloor\end{aligned}\)。
对前半段的函数维护一个前缀和,再用整除分块处理后半段,两段相乘即可。
习题
\(1.\) P3935 Calculating
推导:
\(\begin{aligned}x=\sum\limits_{i=1}^sp_i^{k_i}\end{aligned}\),\(\begin{aligned}f(x)=\prod\limits_{i=1}^s(k_i+1)\end{aligned}\),我们容易发现,\(f(x)\) 表示的其实就是 \(x\) 所有因子的个数,即 \(\begin{aligned}f(x)=\sum\limits_{i=1}^x[i\ |\ x]\end{aligned}\)。
\(\begin{aligned}ans=\sum\limits_{i=l}^rf(i)=\sum\limits_{i=1}^rf(i)-\sum\limits_{i=1}^{l-1}f(i)\end{aligned}\)。对于前者 \(\begin{aligned}\sum\limits_{i=1}^rf(i)\end{aligned}\) 的计算,我们可以利用另外一种解法,即用 \(g(i)\) 表示 \(i\) 在 \(1\sim r\) 中是多少个数的有因子 \(i\),那么很明显 \(\begin{aligned}\sum\limits_{i=1}^rf(i)=\sum\limits_{i=1}^rg(i)\end{aligned}\),同时 \(\begin{aligned}g(i)=\left\lfloor{\dfrac{r}{i}}\right\rfloor\end{aligned}\),因此可得原式 \(\begin{aligned}=\sum\limits_{i=1}^r\left\lfloor{\dfrac{r}{i}}\right\rfloor-\sum\limits_{i=1}^{l-1}\left\lfloor{\dfrac{l-1}{i}}\right\rfloor\end{aligned}\)。
别害怕,黑夜只是白天的前奏
#include <bits/stdc++.h>
#define int long long
#define MOD 998244353
using namespace std;
int H(int n){
int res = 0,l = 1,r;
while(l <= n){
r = n / (n / l);
res += (r - l + 1) * (n / l);
res %= MOD;
l = r + 1;
}
return res;
}
signed main(){
int l,r;scanf("%lld%lld",&l,&r);
printf("%lld",(H(r) + MOD - H(l - 1)) % MOD);
return 0;
}
\(2.\) P2260 [清华集训2012] 模积和
注意题目要求 \(i\ne j\)。我们令 \(n\le m\)(假如大于那就交换一下就行了)。
\(\begin{aligned}ans&=\sum\limits_{i=1}^n(n\bmod i)\sum\limits_{j=1}^m(m\bmod j)-\sum\limits_{i=1}^n(n\bmod i)\times(m\bmod i)\\&=\sum\limits_{i=1}^n(n-i\times\left\lfloor{\dfrac{n}{i}}\right\rfloor)\sum\limits_{j=1}^m(m-j\times\left\lfloor{\dfrac{m}{j}}\right\rfloor)-\sum\limits_{i=1}^n(n-i\times\left\lfloor{\dfrac{n}{i}}\right\rfloor)\times(m-i\times\left\lfloor{\dfrac{m}{i}}\right\rfloor)\\&=(n\times n-\sum\limits_{i=1}^ni\times\left\lfloor{\dfrac{n}{i}}\right\rfloor)\times(m\times m-\sum\limits_{i=1}^mi\times\left\lfloor{\dfrac{m}{i}}\right\rfloor)-\sum\limits_{i=1}^n(n\times m-n\times i\times\left\lfloor{\dfrac{m}{i}}\right\rfloor-m\times i\times\left\lfloor{\dfrac{n}{i}}\right\rfloor+i^2\times\left\lfloor{\dfrac{n}{i}}\right\rfloor\times\left\lfloor{\dfrac{m}{i}}\right\rfloor)\\&=(n\times n-\sum\limits_{i=1}^ni\times\left\lfloor{\dfrac{n}{i}}\right\rfloor)\times(m\times m-\sum\limits_{i=1}^mi\times\left\lfloor{\dfrac{m}{i}}\right\rfloor)-(n^2m-n\times\sum\limits_{i=1}^ni\times\left\lfloor{\dfrac{m}{i}}\right\rfloor-m\times\sum\limits_{i=1}^ni\times\left\lfloor{\dfrac{n}{i}}\right\rfloor+\sum\limits_{i=1}^ni^2\times\left\lfloor{\dfrac{n}{i}}\right\rfloor\times\left\lfloor{\dfrac{m}{i}}\right\rfloor)\end{aligned}\)
\(OK\) 了,式子推完了,我们或许还不知道怎么求的是这一项:\(\begin{aligned}\sum\limits_{i=1}^ni^2\times\left\lfloor{\dfrac{n}{i}}\right\rfloor\times\left\lfloor{\dfrac{m}{i}}\right\rfloor\end{aligned}\)。
我们依旧是分块去求,只不过我们要找的块是 \(\left\lfloor{\dfrac{n}{i}}\right\rfloor\) 和 \(\left\lfloor{\dfrac{m}{i}}\right\rfloor\) 都相等的块,所以把每次更改的 \(r\) 的值改成 min(n / (n / l),m / (m / l)) 即可。关于 \(\begin{aligned}\sum\limits_{i=1}^ni^2\end{aligned}\),有一个结论,\(=\dfrac{n\times(n + 1)\times(2\times n+1)}{6}\),所以每次分完块后用前缀和的思想求一下区间的 \(i^2\) 的和即可。
关于 \(\begin{aligned}\sum\limits_{i=1}^ni^2\end{aligned}=\dfrac{n\times(n + 1)\times(2\times n+1)}{6}\) 的证明:
我们有 \(\dfrac{(n+2)\times(n+1)\times n}{3}-\dfrac{(n+1)\times n\times(n-1)}{3}=(n+1)\times n\)。
使用叠加法,我们有 \(1\times2+2\times3+…+n\times(n+1)=\dfrac{(n+2)\times(n+1)\times n}{3}\)。
即有 \(1^2+2^2+…n^2+(1+2+…+n)=\dfrac{(n+2)\times(n+1)\times n}{3}\),移项,可得:
\(\begin{aligned}\sum\limits_{i=1}^ni^2\end{aligned}=\dfrac{n\times(n + 1)\times(2\times n+1)}{6}\)。
证毕。
预处理一下 \(6\) 在模数下的逆元以节省部分时间,其值为 \(3323403\)。
你听,大海与夕阳之间藏着许多金色的旋律
#include <bits/stdc++.h>
#define MOD 19940417
#define int long long
using namespace std;
int n,m;
int H(int x){
int res = 0,l = 1,r;
while(l <= x){
r = x / (x / l);
res += (l + r) * (r - l + 1) / 2 % MOD * (x / l) % MOD,res %= MOD;
l = r + 1;
}
return res;
}
int H2(){
int res = 0,l = 1,r;
while(l <= n){
r = m / (m / l);
if(r > n) {res += (l + n) * (n - l + 1) / 2 % MOD * (m / l) % MOD,res %= MOD;}
else {res += (l + r) * (r - l + 1) / 2 % MOD * (m / l) % MOD,res %= MOD;}
l = r + 1;
}
return res;
}
int JD(int l,int r){
int a = r * (r + 1) % MOD * (2 * r + 1) % MOD * 3323403 % MOD;
int b = l * (l + 1) % MOD * (2 * l + 1) % MOD * 3323403 % MOD;
return (a - b + MOD) % MOD;
}
int H3(){
int res = 0,l = 1,r;
while(l <= n){
r = min(n / (n / l),m / (m / l));
res += JD(l - 1,r) * (n / l) % MOD * (m / l) % MOD,res %= MOD;
l = r + 1;
}
return res;
}
signed main(){
scanf("%lld%lld",&n,&m);if(n > m) swap(n,m);
int a = ((n * n - H(n)) % MOD + MOD) % MOD;
int b = ((m * m - H(m)) % MOD + MOD) % MOD;
int ans1 = a * b % MOD;
int c = n * n % MOD * m % MOD;
int d = m % MOD * H(n) % MOD;
int e = n % MOD * H2() % MOD;
int f = H3();
int ans2 = ((c - d - e + f) % MOD + MOD) % MOD;
printf("%lld",(ans1 - ans2 + MOD) % MOD);
return 0;
}
积性函数
定义
积性函数:积性函数是指对于所有互质的整数 \(a\) 和 \(b\) 都有性质 \(f(ab)=f(a)f(b)\) 的数论函数,例如欧拉函数 \(\varphi(n)\),莫比乌斯函数 \(\mu(n)\),因数个数函数 \(d(n)\)。
完全积性函数:对于任意整数 \(a\) 和 \(b\) 有性质 \(f(ab)=f(a)f(b)\) 的数论函数。
性质
若 \(f(n)\) 和 \(g(n)\) 都是积性函数,那么以下函数也为积性函数:
\(h(x)=f(x^p)\),\(h(x)=f^p(x)\),\(h(x)=f(x)g(x)\),\(\begin{aligned}h(x)=\sum\limits_{d|x}f(d)g(\dfrac{x}{d})\end{aligned}\)。
常见积性函数
\(\bullet\) 单位函数 \(\epsilon(n)=[n=1]\),别称为“对于狄利克雷卷积的乘法单位”。
\(\bullet\) 幂函数 \(Id^k(n)=n^k\),\(Id^1(n)\) 通常简记为 \(Id(n)\)。
\(\bullet\) 常数函数 \(1(n)=1\)。
\(\bullet\) 因数个数 \(\begin{aligned}d(n)=\sum\limits_{d|n}1\end{aligned}\)。
\(\bullet\) 除数函数 \(\begin{aligned}\sigma_k(n)=\sum\limits_{d|n}d^k\end{aligned}\)。\(k=1\) 时为因数和函数,通常简记为 \(\sigma_n\)。\(k=0\) 时为因数个数函数 \(\sigma_0(n)\)。
\(\bullet\) 欧拉函数 \(\begin{aligned}\varphi(n)=\sum\limits_{i=1}^n[gcd(i,n)=1]\end{aligned}\)。
\(\bullet\) 莫比乌斯函数 \(\mu(n)=\begin{cases}1&n=1\\0&n\ 有平方因子\\(-1)^k&k\ 为\ n\ 的本质不同的质因子个数\end{cases}\)
狄利克雷卷积
定义
定义两个数论函数 \(f(x),g(x)\) 的狄利克雷卷积为:\(\begin{aligned}h(x)=\sum\limits_{d|x}f(d)g(\dfrac{x}{d})=\sum\limits_{ab=x}f(a)g(b)\end{aligned}\)。其和简记为 \(h=f\ast g\)。
性质
\(\bullet\) 满足交换律,结合律,分配律。\(f\ast g=g\ast f\),\((f\ast g)\ast h=f\ast(g\ast h)\),\((f+g)\ast h=f\ast h+g\ast h\)。
\(\bullet\) \(f=g\) 的充要条件是 \(f\ast h=g\ast h\),其中数论函数 \(h(x)\) 要满足 \(h(1)\ne 0\)。
\(\bullet\) \(\epsilon\) 为狄利克雷卷积的单位元,即对于所有的数论函数,有 \((f\ast\epsilon)(n)=f(n)\)。
\(\bullet\) 对于任意一个满足 \(f(x)\ne 0\) 的数论函数,如果有另一个数论函数 \(g(x)\) 满足 \(f\ast g=\epsilon\),则称 \(g(x)\) 是 \(f(x)\) 的逆元,且逆元唯一。
\(\bullet\) 若 \(f,g\) 为积性函数,那么 \(f\ast g\) 为积性函数。
证明:设两个积性函数 \(f(x)\) 和 \(g(x)\),再记 \(h=f\ast g\)。
设 \(gcd(a,b)=1\),则:\(\begin{aligned}h(a)=\sum\limits_{d_1|a}f(d_1)g(\dfrac{a}{d_1}),h(b)=\sum\limits_{d_2|b}f(d_2)g(\dfrac{b}{d_2})\end{aligned}\)。
所以:\(\begin{aligned}h(a)h(b)=\sum\limits_{d_1|a}f(d_1)g(\dfrac{a}{d_1})\sum\limits_{d_2|b}f(d_2)g(\dfrac{b}{d_2})=\sum\limits_{d|ab}f(d)g(\dfrac{ab}{d})=h(ab)\end{aligned}\)。
证毕。
\(\bullet\) \(\begin{aligned}\epsilon=\mu\ast 1\iff\epsilon(n)=\sum\limits_{d|n}\mu(d)\end{aligned}\),\(\begin{aligned}d=1\ast 1\iff d(n)=\sum\limits_{d|n}1\end{aligned}\),\(\begin{aligned}\sigma=id\ast 1\iff\sigma(n)=\sum\limits_{d|n}d\end{aligned}\),\(\begin{aligned}\varphi=\mu\ast id\iff \varphi(n)=\sum\limits_{d|n}d\cdot\mu(\dfrac{n}{d})\end{aligned}\)。
莫比乌斯函数
定义
\(\mu\) 为莫比乌斯函数,其定义为:\(\mu(n)=\begin{cases}1&n=1\\0&n\ 有平方因子\\(-1)^k&k\ 为\ n\ 的本质不同的质因子个数\end{cases}\)
\(n\) 含有平方因子的含义为只要某个质因子出现的次数大于 \(1\) 次,\(\mu(n)\) 就等于 \(0\)。
性质
性质一
莫比乌斯函数是积性函数。
性质二
\(\begin{aligned}\sum\limits_{d|n}\mu(d)=\begin{cases}1&n=1\\0&n\ne 1\end{cases}\end{aligned}\),即可得 \(\begin{aligned}\sum\limits_{d|n}\mu(d)=\epsilon(n),\mu\ast 1=\epsilon\end{aligned}\)。
证明:
设 \(\begin{aligned}n=\prod\limits_{i=1}^sp_i^{c_i},n'=\prod\limits_{i=1}^sp_i\end{aligned}\),则 \(\begin{aligned}\sum\limits_{d|n}\mu(d)=\sum\limits_{d|n'}\mu(d)\end{aligned}\)(因为含有平方因子的因数的 \(\mu\) 为 \(0\))\(\begin{aligned}=\sum\limits_{i=0}^sC_s^i\cdot (-1)^i=(1+(-1))^s\end{aligned}\)(由 二项式定理 得到)。
由此可得只有在 \(s=0\) 即 \(n=1\) 的时候取到值 \(1\),否则为 \(0\),于是 \(\begin{aligned}\sum\limits_{d|n}\mu(d)=[n=1]=\epsilon(n)\end{aligned}\) 以及 \(\mu\ast 1=\epsilon\)。
线性筛求莫比乌斯函数
根据 \(\mu\) 是积性函数求解即可,基本所有的积性函数可以用线性筛解决。
我可不会变成海上的泡沫,我是可以再来一次的人鱼朵朵!
void getMu(){
vis[1] = 1,mu[1] = 1;
for(int i = 2;i <= n;i ++){
if(!vis[i]) Prime[++cnt] = i,mu[i] = -1;
for(int j = 1;j <= cnt and i * Prime[j] <= n;j ++){
vis[i * Prime[j]] = 1;
if(i % Prime[j] == 0){
mu[i * Prime[j]] = 0;
break;
}
mu[i * Prime[j]] = -mu[i];
}
}
}
莫比乌斯变换
设 \(f(n),g(n)\) 为两个数论函数。
根据 \(\mu\ast 1=\epsilon\),可得 \(f=f\ast\epsilon=f\ast(\mu\ast 1)=(f\ast 1)\ast\mu\)。
形式一
如果有 \(\begin{aligned}f(n)=\sum\limits_{d|n}g(d)\end{aligned}\),那么有 \(\begin{aligned}g(n)=\sum\limits_{d|n}\mu(d)f(\dfrac{n}{d})\end{aligned}\)。
这种形式下,数论函数 \(f(n)\) 称为数论函数 \(g(n)\) 的莫比乌斯变换,数论函数 \(g(n)\) 称为数论函数 \(f(n)\) 的莫比乌斯逆变换(反演)。容易看出,数论函数 \(g(n)\) 的莫比乌斯变换,就是将其与常数函数 \(1\) 进行狄利克雷卷积。
证明:
方法一:运用卷积
原问题为:已知 \(f=g\ast 1\),求证 \(g=f\ast \mu\)。
易知 \(f\ast\mu=g\ast 1\ast\mu\),因此 \(f\ast\mu=g\)。(\(1\ast\mu=\epsilon\))
方法二:对原式做数论变换
\(\begin{aligned}\sum\limits_{d|n}\mu(d)f(\dfrac{n}{d})=\sum\limits_{d|n}\mu(d)\sum\limits_{k|\frac{n}{d}}g(k)=\sum\limits_{k|n}g(k)\sum\limits_{d|\frac{n}{k}}\mu(d)=g(n)\end{aligned}\)。
第一步是将已知条件带入得到。第二步是变换求和顺序得到(相当于前者先循环 \(d\) 在循环 \(k\),后者是先循环 \(k\) 在循环 \(d\))。第三部,由性质二可得,只有 \(n=k\) 的时候后者才为 \(1\),其它情况为 \(0\),故只有在 \(k=n\) 的时候才能取到值,即 \(g(n)\)。
证毕。
形式二
如果有 \(\begin{aligned}f(n)=\sum\limits_{n|d}g(d)\end{aligned}\),那么有 \(\begin{aligned}g(n)=\sum\limits_{n|d}\mu(\dfrac{d}{n})f(d)\end{aligned}\)。
证明
\(\begin{aligned}\sum\limits_{n|d}\mu(\dfrac{d}{n})f(d)=\sum\limits_{k=1}^{+\infty}\mu(k)f(kn)=\sum\limits_{i=1}^{+\infty}\mu(k)\sum\limits_{kn|d}g(d)=\sum\limits_{n|d}g(d)\sum\limits_{k|\frac{d}{n}}\mu(k)=g(n)\end{aligned}\)。
拓展
证明 \(\varphi\ast 1=id\):
将 \(n\) 分解质因数得到 \(\begin{aligned}n=\prod\limits_{i=1}^sp_i^{c_i}\end{aligned}\)。因为 \(\varphi\) 是积性函数,故只要证明当 \(n'=p^c\) 时 \(\begin{aligned}\varphi\ast 1=\sum\limits_{d|n'}\varphi(d)=id\end{aligned}\) 成立即可。
因为 \(p\) 时质数,所以 \(d=p^0,p^1…p^c\)。于是我们可得 \(\begin{aligned}\varphi\ast 1=\sum\limits_{d|n}\varphi(d)=\sum\limits_{i=0}^c\varphi(p_i)=1+p^0\times(p-1)+p^1\times (p-1)+p^c\times(p-1)=p^c=id\end{aligned}\)。
该式子两侧同时卷 \(\mu\) 可得到 \(\begin{aligned}\varphi(n)=\sum\limits_{d|n}d\cdot\mu(\dfrac{n}{d})\end{aligned}\)。
反演
莫比乌斯反演结论
\(\begin{aligned}\left[gcd(i,j)=1\right]=\sum\limits_{d|gcd(i,j)}\mu(d)\end{aligned}\)。
证明:运用莫比乌斯函数性质二,其正确性显然。证毕。
同时我们也可以得到 \(\left[gcd(i,j)=1\right]=\epsilon(gcd(i,j))\)。
欧拉反演结论
\(\begin{aligned}gcd(i,j)=\sum\limits_{d|gcd(i,j)}\varphi(d)\end{aligned}\)。
证明详见 我的博客——欧拉函数与欧拉定理。
常见的几种反演形式
以下默认 \(n\le m\)
形式一
\(\begin{aligned}\sum\limits_{i=1}^n\sum\limits_{j=1}^m[gcd(i,j)=1]=\sum\limits_{i=1}^n\sum\limits_{j=1}^m\sum\limits_{d|i}\sum\limits_{d|j}\mu(d)=\sum\limits_{x=1}^n\sum\limits_{i=1}^n\sum\limits_{j=1}^m[d\ |\ i][d\ |\ j]\mu(d)=\sum\limits_{d=1}^n\mu(d)\left\lfloor{\frac{n}{d}}\right\rfloor\left\lfloor{\frac{m}{d}}\right\rfloor\end{aligned}\)
首先 \(O(n)\) 预处理出莫比乌斯函数前缀和,后者二元数论分块即可,单次求解 \(O(\sqrt{n})\)。
习题
\(1.\) P2522 [HAOI2011] Problem b
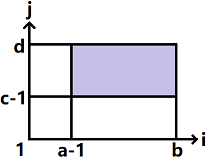
相当于求 \(\begin{aligned}\sum\limits_{i=a}^b\sum\limits_{j=c}^d[gcd(i,j)=k]\end{aligned}\),根据容斥原理,我们可以把它分成四部分,每一部分相当于求 \(\begin{aligned}\sum\limits_{i=1}^n\sum\limits_{j=1}^m[gcd(i,j)=k]=\sum\limits_{i=1}^{\left\lfloor{\frac{n}{k}}\right\rfloor}\sum\limits_{j=1}^{\left\lfloor{\frac{m}{k}}\right\rfloor}[gcd(i,j)=1]\end{aligned}\),然后带入形式一求值,至于分成哪四部分,可以看如图:
外祖母说,最完美的天籁,用热忱和爱才能唱出来!
#include <bits/stdc++.h>
#define N 50004
using namespace std;
int vis[N],mu[N],Prime[N],cnt;
void getMu(){
vis[1] = 1,mu[1] = 1;
for(int i = 2;i <= 50000;i ++){
if(!vis[i]) Prime[++cnt] = i,mu[i] = -1;
for(int j = 1;j <= cnt and Prime[j] * i <= 50000;j ++){
vis[i * Prime[j]] = 1;
if(i % Prime[j] == 0){
mu[i * Prime[j]] = 0;
break;
}
mu[i * Prime[j]] = -mu[i];
}
}
for(int i = 2;i <= 50000;i ++) mu[i] += mu[i - 1];
}
int JD(int n,int m){
if(n > m) swap(n,m);
int res = 0,l = 1,r;
while(l <= n){
r = min(n / (n / l),m / (m / l));
res += (mu[r] - mu[l - 1]) * (n / l) * (m / l);
l = r + 1;
}
return res;
}
int main(){
getMu();int T;scanf("%d",&T);while(T --){
int a,b,c,d,k;scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
printf("%d\n",JD(b / k,d / k) - JD(b / k,(c - 1) / k) - JD((a - 1) / k,d / k) + JD((a - 1) / k,(c - 1) / k));
}
return 0;
}
形式二
\(\begin{aligned}\sum\limits_{i=1}^n\sum\limits_{j=1}^m[gcd(i,j)\in Prime]=\sum\limits_{k\in Prime}\sum\limits_{i=1}^n\sum\limits_{j=1}^m[gcd(i,j)=k]=\sum\limits_{k\in Prime}\sum\limits_{d=1}^{\left\lfloor{\frac{n}{k}}\right\rfloor}\left\lfloor{\frac{n}{kd}}\right\rfloor\left\lfloor{\dfrac{m}{kd}}\right\rfloor\mu(d)=\sum\limits_{T=1}^n\left\lfloor{\dfrac{n}{T}}\right\rfloor\left\lfloor{\dfrac{m}{T}}\right\rfloor\sum\limits_{k|T\land k\in Prime}\mu(\dfrac{T}{k})\end{aligned}\)
最后一步通过换元令 \(T=kd\) 得到。最后一步变换我们实现了可预处理 \(\begin{aligned}\sum\limits_{k|T\land k\in Prime}\mu(\dfrac{T}{k})\end{aligned}\) 的效果,降低了复杂度。预处理方法就是先筛出来所有质数,然后枚举所有质数的倍数即可,处理出来它的前缀和。预处理复杂度 \(O(n\ln n)\),单次求解 \(O(\sqrt{n})\)
习题
\(1.\) P2257 YY的GCD \(\&\) 双倍经验 SP4491 PGCD - Primes in GCD Table
带着歌声,我们一起去往星辰大海吧!
#include <bits/stdc++.h>
#define N 10000000
#define int long long
using namespace std;
int T,n,m,vis[N + 5],mu[N + 5],Prime[N + 5],cnt,f[N + 5];
void getMu(){
vis[1] = 1,mu[1] = 1;
for(int i = 2;i <= N;i ++){
if(!vis[i]) Prime[++cnt] = i,mu[i] = -1;
for(int j = 1;j <= cnt and i * Prime[j] <= N;j ++){
vis[i * Prime[j]] = 1;
if(i % Prime[j] == 0){
mu[i * Prime[j]] = 0;
break;
}
mu[i * Prime[j]] = -mu[i];
}
}
for(int i = 1;i <= cnt;i ++){
for(int j = 1;j * Prime[i] <= N;j ++){
f[j * Prime[i]] += mu[j];
}
}
for(int i = 1;i <= N;i ++) f[i] += f[i - 1];
}
int H(int x){
int res = 0,l = 1,r;
while(l <= x){
r = min(n / (n / l),m / (m / l));
res += (f[r] - f[l - 1]) * (n / l) * (m / l);
l = r + 1;
}
return res;
}
signed main(){
getMu();
scanf("%lld",&T);while(T --){
scanf("%lld%lld",&n,&m);
if(n > m) swap(n,m);
printf("%lld\n",H(n));
}
return 0;
}
形式三
\(\begin{aligned}\sum\limits_{i=1}^n\sum\limits_{j=1}^mgcd(i,j)=\sum\limits_{i=1}^n\sum\limits_{j=1}^m\sum\limits_{d|gcd(i,j)}\varphi(d)=\sum\limits_{d=1}^n\varphi(d)\sum\limits_{i=1}^n[d\ |\ i]\sum\limits_{j=1}^m[d\ |\ j]=\sum\limits_{d=1}^n\left\lfloor{\dfrac{n}{d}}\right\rfloor\left\lfloor{\dfrac{m}{d}}\right\rfloor\varphi(d)\end{aligned}\)
\(O(n)\) 预处理出前缀和 \(\varphi(d)\),单次求解 \(O(\sqrt{n})\)。
习题
\(1.\) SP26017 GCDMAT - GCD OF MATRIX
类似形式一习题一容斥,把它分成四部分。
你小时候都一个人长大,没有伙伴儿么,我都有两条小鱼呢。
#include <bits/stdc++.h>
#define N 50004
#define int long long
#define MOD 1000000007
using namespace std;
int vis[N],phi[N],Prime[N],cnt;
void getPhi(){
vis[1] = 1,phi[1] = 1;
for(int i = 2;i <= 50000;i ++){
if(!vis[i]) Prime[++cnt] = i,phi[i] = i - 1;
for(int j = 1;j <= cnt and i * Prime[j] <= 50000;j ++){
vis[i * Prime[j]] = 1;
if(i % Prime[j] == 0){
phi[i * Prime[j]] = phi[i] * Prime[j];
break;
}
phi[i * Prime[j]] = phi[i] * (Prime[j] - 1);
}
}
for(int i = 1;i <= 50000;i ++) phi[i] = (phi[i] + phi[i - 1]) % MOD;
}
int JD(int n,int m){
if(n > m) swap(n,m);
int res = 0,l = 1,r;
while(l <= n){
r = min(n / (n / l),m / (m / l));
res += (phi[r] - phi[l - 1] + MOD) % MOD * (n / l) * (m / l) % MOD,res %= MOD;
l = r + 1;
}
return res;
}
signed main(){
int T,n,m;scanf("%lld%lld%lld",&T,&n,&m);getPhi();while(T --){
int a,b,c,d;scanf("%lld%lld%lld%lld",&a,&b,&c,&d);a -= 1,b -= 1;
printf("%lld\n",((JD(c,d) - JD(a,d) - JD(c,b) + JD(a,b)) % MOD + MOD) % MOD);
}
return 0;
}
形式四
首先我们先了解一个结论:\(\begin{aligned}d(ij)=\sum\limits_{x|i}\sum\limits_{y|j}[gcd(x,y)=1]\end{aligned}\)。
证明
由于 \(d\) 函数是积性函数,所以我们不妨将每一个质因子分开考虑:
设 \(i,j\) 分别含有 \(a,b\) 个质因子 \(p\),显然等式左侧可以选择的因子的个数为 \(a+b+1\) 个。对于右侧而言,显然也有 \(a+b+1\) 中,即要么 \(x=1\),\(y\) 的选择方法为 \(b\) 个;要么 \(y=1\),\(x\) 的选择方法为 \(a\) 个,要么二者都为 \(1\)。因此等式两边相等。
证毕。
6。啥时候想回来补就回来补。

 浪花是海的笑声,星星是天空的梦,这首是人鱼的歌。
浪花是海的笑声,星星是天空的梦,这首是人鱼的歌。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号