KMP
前置
关于字符串的一些定义:
对于一字符串 \(s\):
前缀:从串首到某一位置 \(i\) 的一个子串,即 \(s[0…i]\)。真前缀:除了 \(s\) 外的其他前缀。
后缀:从某一位置 \(i\) 到串末的一个子串,即 \(s[i…|s|-1]\)。真后缀:除了 \(s\) 外的其他后缀。
前缀函数
定义
定义一字符串 \(s\) 的前缀函数 \(\pi[i]=\max\limits_{k\in[0,i]}\{k:s[0…k-1]=s[i-(k-1)…i]\}\)。
通俗来讲,即我们要找字符串 \(s\) 最长的相等的真前缀和真后缀的长度。
举个例子:对于一个字符串 abcabd。
\(\pi[0]=0\)。
\(\pi[1]=0\)。
\(\pi[2]=0\)。字符串 a、ab、abc 都没有相等的真前缀和真后缀。
\(\pi[3]=1\),因为此时最前面的 a,与最后面的 a 匹配,长度为 \(1\)。
\(\pi[4]=2\),因为此时最前面的 ab,与最后面的 ab 匹配,长度为 \(2\)。
\(\pi[5]=0\),此时最前面的和最后面的无法匹配。
计算前缀函数
暴力做法:
for(int i = 1;i < n;i ++){
for(int j = i;j >= 0;j --){
if(s.substr(0,j) == s.substr(i - j + 1,j)){
pi[i] = j;
break;
}
}
}
都能看懂,时间复杂度 \(O(n^3)\),考虑优化。
优化1
我们很容易的可以得到,相邻的两个前缀函数最多增加 \(1\)。
即对于前缀 \(s[0…i]\) 的前缀函数为 \(\pi[i]\) 时,我们只有当 \(s[i+1]=s[\pi[i]]\) 时,才可以得到 \(\pi[i+1]=\pi[i]+1\)。
所以,我们在第二层循环时,我们不必从 \(i\) 开始,我们仅仅从 \(pi[i-1]+1\) 开始即可,因为他的前缀函数最多只可能比 \(pi[i-1]\) 大 \(1\)。
for(int i = 1;i < n;i ++){
for(int j = pi[i - 1] + 1;j >= 0;j --){
if(s.substr(0,j) == s.substr(i - j + 1,j)){
pi[i] = j;
break;
}
}
}
优化2

假设此时,我们找到了子串 \(s[0…i]\) 的前缀函数 \(\pi[i]\)。

那么此时就判断 \(s[i+1]\) 是否等于 \(s[\pi[i]]\),即图中紫色部分。
那么如果不等于呢?我们的思路就是,找到一个最大的 \(j\),使得同种绿色的部分相等,然后再判断红色的部分是否相等即可。注意这个 \(j\) 此时一定小于 \(\pi[i]\)(根据优化 \(1\) 可以得到)。
那么怎么找到这个最大的 \(j\) 呢?
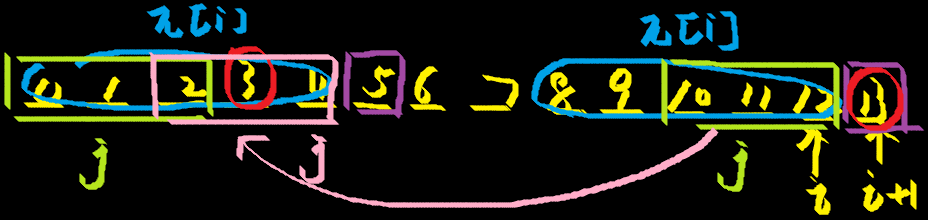
我们发现,对于第二个绿色部分的那一片区域,由于有着上一次计算的 \(\pi[i]\),因此可以转化到粉色部分,那么问题就可以转化为找到一个最大的 \(j\) 使得第一个绿色部分等于粉色部分。我们发现,这不就相当于 \(s[0…\pi[i]-1]\) 的前缀函数吗。
此时我们找到 \(j\) 了,所以我们就判断两个红色的位置是否相等即可。如果还是不相等,那就继续按着这个思路一直往下走就行,知道找到了相等的或者 \(j=0\) 的时候结束。
具体实现请看代码:
for(int i = 1;i < n;i ++){
int j = pi[i - 1];
while(j > 0 and s[i] != s[j]) j = pi[j - 1];
if(s[i] == s[j]) j ++;
pi[i] = j;
}
应用
KMP
所谓 KMP 算法,即是一种高效的模式匹配的一种算法模式匹配,说直白就是找寻子字符串在主字符串的位置。
思路
我们要求 \(s\) 在 \(t\) 中的出现位置,构造一个字符串 \(s+\#+t\),\(\#\) 为一个即不出现在 \(s\) 也不出现在 \(t\) 中的一个分隔符。我们现在来看一下这个大字符串 \(t\) 这一部分前缀函数的一个意义:由于分隔符的存在,后面部分的 \(\pi[i]\) 不可能会大于 \(|s|\),故当 \(\pi[i]=|s|\) 时,意味着 \(s\) 完整的出现在该位置(注意为右端点为 \(i\),且是相对于这个大字符串而言)。
例题 P3375 【模板】KMP
可以看一下代码来理解 KMP。
#include <bits/stdc++.h>
#define N 2000006
using namespace std;
string s,t;int kmp[N];
int main(){
cin >> t >> s;
for(int i = 1;i < s.size();i ++){
int j = kmp[i - 1];
while(s[i] != s[j] and j > 0) j = kmp[j - 1];
kmp[i] = j;if(s[i] == s[j]) kmp[i] ++;
}
t = s + "#" + t;
for(int i = s.size() + 1;i < t.size();i ++){
int j = kmp[i - 1];
while(t[i] != t[j] and j > 0) j = kmp[j - 1];
kmp[i] = j;if(t[i] == t[j]) kmp[i] ++;
if(kmp[i] == s.size()) printf("%d\n",i - s.size() * 2 + 1);
}
for(int i = 0;i < s.size();i ++) printf("%d ",kmp[i]);
return 0;
}
注意:第 \(12\) 行、\(18\) 行是 while,我有一道题就因为写成 if 了而调了两个小时。
习题
1. CF1200E Compress Words
依次读入这 \(n\) 个字符串,即当前累计的答案为 \(ans\),当前需要处理的字符串为 \(s\)。我们需要找的是最长的 \(s\) 的前缀和 \(ans\) 的后缀相等的长度,所以我们定义一个新的字符串 \(t=s+\#+ans\),然后再计算前缀函数即可。
注意一个点,\(ans\) 会累计的越来越大,因此 \(t\) 也将会越来越长,导致再计算前缀函数的时候复杂度越来越大。因此我们每次 \(t\) 不用加上整个 \(ans\) 字符串,而是只取后面的一些部分即可,这个长度为 \(min\{|s|,|ans|\}\)。
潜龙腾渊凌霄上,尘世无名誓不休!
#include <bits/stdc++.h>
#define N 1000006
using namespace std;
int n,kmp[N];string ans;
int main(){
scanf("%d",&n);cin >> ans;
n --;while(n --){
string s;cin >> s;int len = min(s.size(),ans.size());kmp[0] = 0;
string t = s + "#" + ans.substr(ans.size() - len,len);
for(int i = 1;i < t.size();i ++){
int j = kmp[i - 1];
while(t[j] != t[i] and j > 0) j = kmp[j - 1];
kmp[i] = j;if(t[j] == t[i]) kmp[i] ++;
}
for(int i = kmp[t.size() - 1];i < s.size();i ++) ans += s[i];
}
cout << ans;
return 0;
}
2. P4824 [USACO15FEB] Censoring S
类似模板题的题目里让处理的第一个问题,我们找到一个位置以后,直接把字符串里的处在这一个位置的字符串 \(T\) 删去,然后在从删去后当前位置的下标继续向后计算前缀函数,如此往复即可。具体实现请看代码。
我身何畏风雨来?风雨渡江,岂不快哉!
#include <bits/stdc++.h>
#define N 2000006
using namespace std;
int kmp[N];string s,t;
int main(){
cin >> s >> t;s = t + "#" + s;
for(int i = 1;i < s.size();i ++){
int j = kmp[i - 1];
while(s[j] != s[i] and j > 0) j = kmp[j - 1];
kmp[i] = j;if(s[i] == s[j]) kmp[i] ++;
if(kmp[i] == t.size() and i != t.size() - 1) s.erase(i - t.size() + 1,t.size()),i -= t.size();
}
s.erase(0,t.size() + 1);cout << s << endl;
return 0;
}
3. UVA12467 Secret Word
定义 \(s'\) 为字符串 \(s\) 反转后的字符串,那么令 \(t=s+\#+s'\),然后再求出来 \(s'\) 所在区间内的最大的前缀函数 \(\pi_{max}\) 即为所求,只不过要倒序输出 \(s[0…\pi_{max}-1]\)。
振银鳞,赴虞渊,再历星天万千年。
#include <bits/stdc++.h>
#define N 2000006
using namespace std;
int T,kmp[N];string s;
int main(){
scanf("%d",&T);while(T --){
cin >> s;string t = s;reverse(t.begin(),t.end());
s = s + "#" + t;int num = 0;
for(int i = 1;i < s.size();i ++){
int j = kmp[i - 1];
while(j > 0 and s[j] != s[i]) j = kmp[j - 1];
kmp[i] = j;if(s[j] == s[i]) kmp[i] ++;
if(i > t.size()) num = max(num,kmp[i]);
}
for(int i = num - 1;i >= 0;i --) cout << s[i];puts("");
}
return 0;
}
4. CF471D MUH and Cube Walls
思路:我们计算出 \(a\),\(b\) 数组每相邻两位的方差,分别记为 \(p\),\(q\),那么此题就可以转化为 \(q\) 在 \(p\) 中出现的次数。直接套 \(KMP\) 即可。另外需要注意一些细节的东西。
此战,只有彼我存亡,绝无两败俱伤。
#include <bits/stdc++.h>
#define N 400005
using namespace std;
int n,m,num,a[N],jd[N],kmp[N];
int main(){
scanf("%d%d",&n,&m);a[m - 1] = 1e9;if(m == 1){printf("%d",n);return 0;}
for(int i = 1;i <= n;i ++) {scanf("%d",&jd[i]);if(i != 1) a[i + m - 2] = jd[i] - jd[i - 1];}
for(int i = 1;i <= m;i ++) {scanf("%d",&jd[i]);if(i != 1) a[i - 2] = jd[i] - jd[i - 1];}
for(int i = 1;i <= n + m - 2;i ++){
int j = kmp[i - 1];
while(j > 0 and a[i] != a[j]) j = kmp[j - 1];
kmp[i] = j;if(a[i] == a[j]) kmp[i] ++;
if(i >= m and kmp[i] == m - 1) num ++;
}
printf("%d",num);
return 0;
}
5. POJ2752 Seek the Name, Seek the Fame
输出整个字符串的所有前缀函数。
剑成如飚,意裁风刀。
#include <iostream>
#include <cstdio>
#include <string>
#define N 400005
using namespace std;
int kmp[N],ans[N],cnt;string s;
int main(){
while(cin >> s){
int n = s.size();cnt = 0;
for(int i = 1;i < n;i ++){
int j = kmp[i - 1];
while(j && s[i] != s[j]) j = kmp[j - 1];
kmp[i] = j;if(s[i] == s[j]) kmp[i] ++;
}
while(kmp[n - 1]) ans[++cnt] = kmp[n - 1],kmp[n - 1] = kmp[kmp[n - 1] - 1];
for(int i = cnt;i >= 1;i --) printf("%d ",ans[i]);printf("%d ",n);puts("");
}
return 0;
}
6. UVA12604 Caesar Cipher
简要说一下题意:对于 \(T\) 组数据,每组数据都有三个字符串 \(a\),\(w\),\(s\)。字符串 \(a\) 表示一个字符表(这个字符表包含小写字母、大写字母、数字)。我们定义 “移位” 表示 \(a\) 中字符串中的每一个字符都变为它的下一个字符(最后一个变成第一个),然后还可以在这个状态下再次 “移位”,也就是字符串 \(a\) 一共有 \(|a|\) 中状态。\(w\) 也可以根据 \(a\) 中的移位去改变自己的状态。例如:\(a=E0CF2\),那么第一次移位后,\(a=0CF2E\),那么此时原 \(E\to 0\),\(0\to C\),\(C\to F\),\(F\to 2\),\(2\to E\);假设 \(w=EC2\),那么此时 \(w=0FE\)。现在,我们要找出 \(w\) 的所有状态(包括原状态)在 \(s\) 中的出现次数。我们记录所有的 某个状态在 \(s\) 中只出现一次 的所有状态。假如说没有,则输出 no solution。假如只有一个,则输出 unique: #(# 表示移位的次数)。假如有两个及以上,则先输出 ambiguous: ,然后在从小到大输出满足条件的移位的次数,中间用空格隔开。
注意:行末不能有多余空格。可以参考代码 \(28\),\(29\) 行。
解析:我们暴力枚举 \(a\) 的所有状态,进而去得到 \(w\) 的所有状态,然后计算前缀函数即可。
神龙显昭——直取太霄!
#include <bits/stdc++.h>
#define N 1000006
using namespace std;
unordered_map < char , char > p;
int T,kmp[N],cnt,num,ans[N];
string a,w,s;
int main(){
scanf("%d",&T);while(T --){
cin >> a >> w >> s;cnt = 0;
for(int opt = 0;opt < a.size();opt++){
for(int i = 0;i < a.size();i ++) p[a[i]] = a[(opt + i) % a.size()];
string t = "";for(int i = 0;i < w.size();i ++){string jd;jd = p[w[i]],t += jd;}
t = t + "#" + s;num = 0;
for(int i = 1;i < t.size();i ++){
int j = kmp[i - 1];
while(j > 0 and t[i] != t[j]) j = kmp[j - 1];
kmp[i] = j;if(t[i] == t[j]) kmp[i] ++;
if(i != w.size() - 1 and kmp[i] == w.size()) num ++;
}
if(num == 1) ans[++cnt] = opt;
}
if(cnt == 0) puts("no solution");
else if(cnt == 1) printf("unique: %d\n",ans[1]);
else{
printf("ambiguous:");
for(int i = 1;i <= cnt;i ++) printf(" %d",ans[i]);puts("");
}
}
return 0;
}
7. P2375 [NOI2014] 动物园
值得练习,非常典的一道题。一定要自己思考。
我们的思路是,记录字符串每一个前缀子串的前缀函数的数量,记为 \(num_i\)。每次查询时,我们只要对于每一个子串的前缀函数一直递归到 \(\pi_i\times 2\le i+1\) 时就可以了,然后答案加上对应的 \(num_i\)。
不过我们做完之后,发现会 TLE,为什么呢?假设这个字符串有 \(1000000\) 个 \(a\),模拟一下,你就知道为什么会 \(TLE\) 了。
那怎么解决呢?我们每次递归玩找到了 \(j\) 后,保留这个 \(j\) 值到下一个子串。因为这个 \(j\) 已经满足了 \(j\times 2\le i+1\)。然后通过这个值在去找满足当前情况的 \(j\) 就行了。
可能你还会有不懂的地方,自己想想。如果你对 \(KMP\) 理解透彻的话,想通这个题是没有什么问题的。
怀必死之志,搏转圜之机!
#include <bits/stdc++.h>
#define N 1000006
#define int long long
#define MOD 1000000007
using namespace std;
int T,kmp[N],num[N],ans;string s;
signed main(){
scanf("%lld",&T);while(T --){
cin >> s;kmp[0] = 0,ans = 1;memset(num,0,sizeof(num));num[1] = 1;
for(int i = 1;i < s.size();i ++){
int j = kmp[i - 1];
while(s[j] != s[i] and j > 0) j = kmp[j - 1];
kmp[i] = j;if(s[j] == s[i]) j ++,kmp[i] ++;
num[i + 1] = num[j] + 1;
}
int j = 0;
for(int i = 1;i < s.size();i ++){
while(s[j] != s[i] and j > 0) j = kmp[j - 1];
if(s[j] == s[i]) j ++;
if(j * 2 > i + 1) j = kmp[j - 1];
ans = ans * (num[j] + 1) % MOD;
}
printf("%lld\n",ans);
}
return 0;
}
字符串的周期
对于一个 \(1\le p\le |s|\),若对于所有的 \(i\in[0,|s|-p-1]\) 有 \(s[i]=s[i+p]\),则称 \(p\) 是 \(s\) 的一个周期。
显然,稍加思考,对于 \(s\) 的最小周期为 \(|s|-\pi[|s|-1]\)。
例题 P4391 无线传输
问我来处,青野之梗;问我去处,冥冥天穹;谁与我同游……白首一仙翁。
#include <bits/stdc++.h>
#define N 1000006
using namespace std;
int kmp[N],L;string s;
int main(){
scanf("%d",&L);cin >> s;
for(int i = 1;i < s.size();i ++){
int j = kmp[i - 1];
while(j > 0 and s[i] != s[j]) j = kmp[j - 1];
kmp[i] = j;if(s[i] == s[j]) kmp[i] ++;
}
printf("%d",L - kmp[L - 1]);
return 0;
}
习题
1. P3435 [POI2006] OKR-Periods of Words
题目说的是类似周期的东西,所以我们先往周期那里去想。
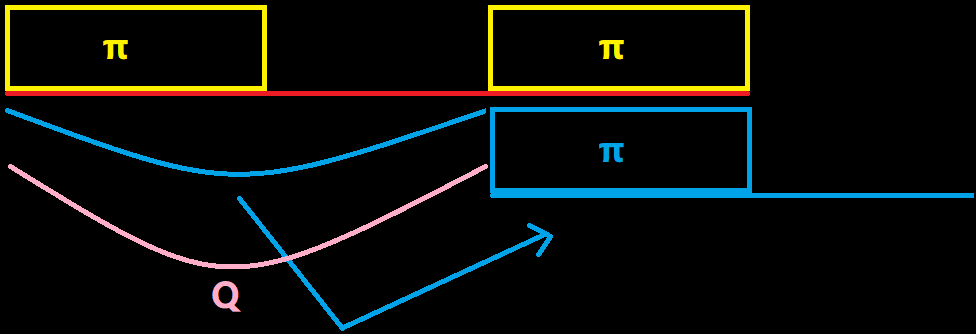
从这里我们可以发现,当我们找到一个字符串的一个前缀函数后(黄色部分),我们把这个蓝色(粉色)的部分,复制到他们的后面,这样的话原字符串就是当前大字符串的一个子串,也就是题目中所说的 \(Q\)。题目中说要让 \(Q\) 最大,所以我们需要让让 \(\pi\) 最小才能让这个 \(Q\) 最大。转换一下,也就是要去求这个 \(\pi\) 的最小值,那么就可以转化为每次求他的最小前缀函数。
那么最小前缀函数怎么求呢?
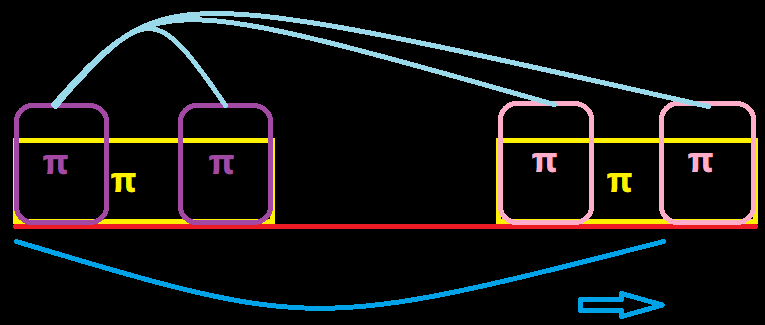
现在大概就懂了吧,紫色和粉色都是一样的,因此我们就一次求前缀函数的前缀函数,找到最小的且不为 \(0\) 的那个就行了。
所以我们就还是先把每一个的最大前缀函数求出来,然后在一次去遍历最小的前缀函数就行。不过如果每次都暴力求最小前缀函数的话,会 TLE,因此我们就加一个记忆化,每次求出来最小前缀函数后就赋值给这个字符串的前缀函数即可,这样在后续求解其他的最小前缀函数的如果需要用到就可以直接到这个最小的前缀函数。
处身浮世,谁又不是命在倏忽?但叶落归根,生生无穷,此我族之道。
#include <bits/stdc++.h>
#define N 1000006
#define int long long
using namespace std;
int n,num,kmp[N];string s;
signed main(){
scanf("%lld",&n);cin >> s;
for(int i = 1;i < s.size();i ++){
int j = kmp[i - 1];
while(s[j] != s[i] and j > 0) j = kmp[j - 1];
kmp[i] = j;if(s[j] == s[i]) kmp[i] ++;
}
for(int i = 1;i < s.size();i ++){
int j = kmp[i];if(j == 0) continue;
while(kmp[j - 1]) j = kmp[j - 1];
kmp[i] = j,num += i + 1 - j;
}
printf("%lld",num);
return 0;
}
2. HDU3746 Cyclic Nacklace
首先,特判 \(kmp[|s|-1]=0\) 的情况,输出 \(|s|\)。
其次,计算最小周期 \(T=|s|-\pi[|s|-1]\),假设 \(|s| \bmod T=0\),那么证明已经满周期,输出 \(0\)。
否则,输出 \(T-n \bmod T\)。
生当奋飞,腾必九霄。
#include <iostream>
#include <cstdio>
#include <string>
#define N 100005
using namespace std;
int T,kmp[N];string s;
int main(){
scanf("%d",&T);while(T --){
cin >> s;int n = s.size();
for(int i = 1;i < n;i ++){
int j = kmp[i - 1];
while(j && s[i] != s[j]) j = kmp[j - 1];
kmp[i] = j;if(s[i] == s[j]) kmp[i] ++;
}
if(kmp[n - 1] == 0) printf("%d\n",n);
else{
if(n % (n - kmp[n - 1]) == 0) printf("%d\n",0);
else printf("%d\n",n - kmp[n - 1] - n % (n - kmp[n - 1]));
}
}
return 0;
}
3. UVA11452 Dancing the Cheeky-Cheeky
与上题类似,计算一个字符串的周期。虽然题目说这个周期必须在字符串中出现了 \(2\) 至 \(3\)(包含 \(2\),但是不包含 \(3\)),不过我们可以发现,不管我们周期计算的大小是多少,对我们的结果都不会造成影响,因此直接计算最短周期周期输出在当前周期下紧接着给定的字符串的 \(8\) 个字符即可。
所谓兴灭继绝,就是从一族最险最痛的伤口上,将往事,一一重建。
#include <iostream>
#include <cstdio>
#include <string>
#define N 100005
using namespace std;
int T,kmp[N];string s;
int main(){
scanf("%d",&T);while(T --){
cin >> s;int n = s.size();
for(int i = 1;i < n;i ++){
int j = kmp[i - 1];
while(j && s[i] != s[j]) j = kmp[j - 1];
kmp[i] = j;if(s[i] == s[j]) kmp[i] ++;
}
if(n % (n - kmp[n - 1]) == 0){
int i = 0,cnt = 0;while(cnt < 8){
cout << s[i];i ++;cnt ++;
if(i == n - kmp[n - 1]) i = 0;
}
}
else{
int i = n % (n - kmp[n - 1]),cnt = 0;while(cnt < 8){
cout << s[i];i ++;cnt ++;
if(i == n - kmp[n - 1]) i = 0;
}
}
puts("...");
}
return 0;
}
4.SP34020 ADAPET - Ada and Pet
基本板题,不做解析。注意事项请看“计算循环节”的第二段。
若你在世间不曾见我,想必那时,我已飞度天外。
#include <bits/stdc++.h>
#define N 500005
#define int long long
using namespace std;
int T,kmp[N],k;char s[N];
signed main(){
scanf("%lld",&T);while(T --){
scanf("%s %lld",s,&k);int n = strlen(s);
for(int i = 1;i < n;i ++){
int j = kmp[i - 1];
while(j && s[i] != s[j]) j = kmp[j - 1];
kmp[i] = j;if(s[i] == s[j]) kmp[i] ++;
}
printf("%lld\n",n + (n - kmp[n - 1]) * (k - 1));
}
return 0;
}
统计每个前缀的出现次数
给定一个字符串 \(s\),求 \(s\) 的所有前缀在字符串中的出现次数。我们可以用如下方法求解:
for(int i = 0;i < s.size();i ++) ans[kmp[i]] ++;
for(int i = s.size() - 1;i > 0;i --) ans[kmp[i - 1]] += ans[i];
for(int i = 0;i <= s.size();i ++) ans[i] ++;
解释:我们优先统计每个字符串前缀函数在 \(kmp\) 数组(也就是 \(\pi\) 数组)中出现了都少次,然后在统计答案:如果前缀长度为 \(i\) 出现了 \(ans_i\) 次,那么就把该值叠加到其最长的前缀函数的子串出现的次数中。最后对每个前缀 \(+1\) 以统计原始的前缀。
如果有疑问的话,自己手动搓一组数据(可以参考下面例题的样例)就行。
例题 CF432D Prefixes and Suffixes
大道并非一条,哪有那么多过来人能一一指路——我要自己走。
#include <bits/stdc++.h>
#define N 100005
using namespace std;
int kmp[N],ans[N];string s;
struct W{int a,b;}w[N];
bool cmp(W a,W b) {return a.a < b.a;}
int main(){
cin >> s;
for(int i = 1;i < s.size();i ++){
int j = kmp[i - 1];
while(j > 0 and s[i] != s[j]) j = kmp[j - 1];
kmp[i] = j;if(s[i] == s[j]) kmp[i] ++;
}
for(int i = 0;i < s.size();i ++) ans[kmp[i]] ++;
for(int i = s.size() - 1;i > 0;i --) ans[kmp[i - 1]] += ans[i];
for(int i = 0;i <= s.size();i ++) ans[i] ++;
int j = s.size(),cnt = 0;
while(j) w[++cnt].a = j,w[cnt].b = ans[j],j = kmp[j - 1];
printf("%d\n",cnt);sort(w + 1,w + cnt + 1,cmp);
for(int i = 1;i <= cnt;i ++) printf("%d %d\n",w[i].a,w[i].b);
return 0;
}
习题
1. HDU3336 Count the string
就是板子,只是为了让你们加深一下印象重新打一遍。
我虽年弱,但龙有逆鳞,犯之者死。
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#define N 200005
#define MOD 10007
using namespace std;
int T,n,kmp[N],ans[N];string s;
int main(){
scanf("%d",&T);while(T --){
scanf("%d",&n);cin >> s;
for(int i = 1;i < s.size();i ++){
int j = kmp[i - 1];
while(j > 0 && s[j] != s[i]) j = kmp[j - 1];
kmp[i] = j;if(s[j] == s[i]) kmp[i] ++;
}
int num = 0;memset(ans,0,sizeof(ans));
for(int i = 0;i < s.size();i ++) ans[kmp[i]] ++;
for(int i = s.size() - 1;i > 0;i --) ans[kmp[i - 1]] += ans[i],ans[kmp[i - 1]] %= MOD;
for(int i = 1;i <= s.size();i ++) num += ans[i] + 1,num %= MOD;
printf("%d\n",num);
}
return 0;
}
2. HDU1686 Oulipo
是的,还是板子。思路是令一个新的字符串等于 \(s+\#+t\),计算前缀出现次数即可。
欲破举世沉疴——于我一剑下。
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#define N 2000006
using namespace std;
int T,kmp[N],ans[N];
string s,t;
int main(){
scanf("%d",&T);while(T --){
cin >> s >> t;t = s + "#" + t;
memset(ans,0,sizeof(ans));
for(int i = 1;i < t.size();i ++){
int j = kmp[i - 1];
while(j && t[i] != t[j]) j = kmp[j - 1];
kmp[i] = j;if(t[i] == t[j]) kmp[i] ++;
}
for(int i = 0;i < t.size();i ++) ans[kmp[i]] ++;
for(int i = t.size() - 1;i > 0;i --) ans[kmp[i - 1]] += ans[i];
printf("%d\n",ans[s.size()]);
}
return 0;
}
一个字符串中本质不同的子串数目
使用 \(kmp\) 解决的话不太高效,总复杂度为 \(O(n^2)\),数据大的需要使用 \(SA\) 或 \(SAM\) 来解决。但是如果数据弱的话我们可以直接使用 \(kmp\) 来解决。
我们将迭代的解决问题。即,我们知道当前字符串 \(s\) 本质不同的子串的个数,如果在它的后面加上一个字符 \(c\),会有多少个新的子串出现?
我们构造一字符串 \(t=s+c\),并将其反转得到 \(t'\)。现在我们只需要计算有多少 \(t'\) 的前缀没有在其余地方出现即可。我们如果计算出了 \(t'\) 前缀函数的最大值 \(\pi_{max}\),那么自然其他所有更短的前缀也就出现了。即,当添加一个新字符后新出现的子串数目为 \(|s|+1-\pi_{max}\)。
例题 P2408 不同子串个数
注:用此方法做的话只能得到 \(60\) 分,正解使用 \(SA\) 或 \(SAM\),因为我没有找到其他题,因此先凑活着用吧。
不必将我视作需要相让的稚子,像你这样的敌人,我不止有一个。
#include <bits/stdc++.h>
#define N 100005
using namespace std;
int n,kmp[N],f[N];
string s;
int main(){
scanf("%d",&n);cin >> s;f[0] = 1;
for(int i = 1;i < s.size();i ++){
string t = s.substr(0,i + 1);reverse(t.begin(),t.end());
int num = 0;
for(int j = 1;j < t.size();j ++){
int k = kmp[j - 1];
while(k > 0 and t[j] != t[k]) k = kmp[k - 1];
kmp[j] = k;if(t[j] == t[k]) kmp[j] ++;
num = max(num,kmp[j]);
}
f[i] = f[i - 1] + i + 1 - num;
}
printf("%d",f[s.size() - 1]);
return 0;
}
字符串的压缩
给定一字符串 \(s\),我们希望找到一个最短的字符串 \(t\),使得 \(s\) 可以被 \(t\) 的一份或者多份拷贝的拼接表示。
结论:通过计算该前缀函数的最后一个值 \(\pi[|s|-1]\),我们定义 \(k=|s|-\pi[|s|-1]\)。如果 \(k\) 能被 \(n\) 整除,那么 \(k\) 就是答案;否则不存在一个有效的压缩,答案为 \(n\)。
简单证明:根据前缀函数的定义,我们知道该字符串长度为 \(|s|-k\) 的前缀等于其后缀,那么这就意味着随后一个块和倒数第二个块相等,倒数第二个块和倒数第三个块相等,等等。
对于证明该值为最优解:假设有一个更小的 \(k\),那么前缀函数的最后一个值 \(\pi[|s|-1]\) 一定会比 \(|s|-k\) 要大,与现有条件不符,因此 \(k\) 就是最优解。
例题 POJ2406 Power Strings
谁共我,万丈颠波!
#include <iostream>
#include <cstdio>
#include <string>
#define N 1000006
using namespace std;
int kmp[N];string s;
int main(){
while(cin >> s){
if(s == ".") return 0;
for(int i = 1;i < s.size();i ++){
int j = kmp[i - 1];
while(j && s[i] != s[j]) j = kmp[j - 1];
kmp[i] = j;if(s[i] == s[j]) kmp[i] ++;
}
if(kmp[s.size() - 1] != 0 and s.size() % (s.size() - kmp[s.size() - 1]) == 0) printf("%d\n",s.size() / (s.size() - kmp[s.size() - 1]));
else puts("1");
}
}
习题
1. POJ1961 Period
类似板子。
何消天涯风共雪?前尘为梦;何陟人间雨翻云?来日方长。
#include <iostream>
#include <cstdio>
#include <string>
#define N 1000006
using namespace std;
int n,cnt,kmp[N];string s;
int main(){
while(1){
cin >> n;if(n == 0) return 0;cin >> s;
cnt ++;printf("Test case #%d\n",cnt);
for(int i = 1;i < s.size();i ++){
int j = kmp[i - 1];
while(j && s[i] != s[j]) j = kmp[j - 1];
kmp[i] = j;if(s[i] == s[j]) kmp[i] ++;
if(kmp[i] != 0 && (i + 1) % (i + 1 - kmp[i]) == 0) printf("%d %d\n",i + 1,(i + 1) / (i + 1 - kmp[i]));
}puts("");
}
}
计算循环节
直接上例题。
例题 HDU6740 MUV LUV EXTRA
我们的思路是把小数点后面的部分反转,然后依次求解每个前缀的前缀函数,那么循环节就是那么对应的答案即为 \(a\times(i+1)-b\times(i+1-kmp_i)\)。原因:我们想让这个结果最大,那么就应该让 \(b\times(i+1-kmp_i)\) 最小,那么就应该让 \(kmp_i\) 最大,故求最长的前缀函数就可以。自己可以手动模拟一下。
有一个注意的东西,我不知道问什么。输入字符串的直接用 cin 输入字符串是会 TLE 的,但是如果使用 scanf 输入一个字符数组就可以了。另外,一个字符数组的长度可以用 strlen(s) 得到,但是它的时间复杂度是 \(O(n)\) 的,而一个字符串 \(s.size()\) 的时间复杂度是 \(O(1)\) 的。但是用前者会 TLE,后者可以 AC。注意一下就行了。(话说我因为这个东西对着题解调了两个小时?)
向世间,破尽尘骸一剑中。
#include <iostream>
#include <cstdio>
#include <string>
#include <algorithm>
#include <cstring>
#define N 10000007
using namespace std;
int num,kmp[N],cnt;
long long a,b;
char s[N],t[N];
int main(){
while(~scanf("%lld%lld",&a,&b)){
scanf("%s",s);long long num = a - b;int cnt = -1;
for(int i = strlen(s) - 1;i >= 0;i --){
if(s[i] == '.') break;
t[++cnt] = s[i];
}
for(int i = 1;i <= cnt;i ++){
int j = kmp[i - 1];
while(j && t[i] != t[j]) j = kmp[j - 1];
kmp[i] = j;if(t[i] == t[j]) kmp[i] ++;
num = max(num,a * (i + 1) - b * (i + 1 - kmp[i]));
}
printf("%lld\n",num);
}
return 0;
}
KMP 与 DP 的结合
不会,等啥时候重温了 \(DP\) 在写。(一般立这种 \(flag\) 可能就不写了)

 悬名天下,我昭四方。
悬名天下,我昭四方。
