园龄：1年11个月粉丝：40 关注：22

可持久化线段树

前置

线段树

引入

可持久化线段树模板题：P3834 【模板】可持久化线段树 2

题目大意：给定由 $n$ 个整数构成的序列 $a$ ，对于一区间 $[l, r]$ 查询其第 $k$ 小值。

思路：每一次加入新的数都建一个线段树，保存所有历史版本，以便查询区间第 $k$ 小。

解释

思路

整体思路就是逐一插入每一个数字，然后利用前缀和的思想求解。

由于 $a_{i} \leq 10^{9}$ ，所以需要将所有数离散化之后在进行操作。

我们通过样例来模拟：

 5 5
25957 6405 15770 26287 26465 
2 2 1
3 4 1
4 5 1
1 2 2
4 4 1

离散化后的结果： $25957 \to 3, 6405 \to 1, 15770 \to 2, 26287 \to 4, 26465 \to 5$ 。

〇首先建一棵空树：

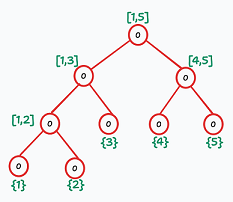
然后依次将每个离散化后的数字的编号插入到它的位置上，然后把所有包括它的区间的 $a n s$ 都 $+ 1$ 。

① 加入 $25957 \to 3$ ② 加入 $6405 \to 1$ ③ 加入 $15770 \to 2$ ④ 加入 $26287 \to 4$ ⑤ 加入 $26465 \to 5$

假设要查询 $[2, 5]$ 中的第 $3$ 大的数。我们首先把第 ① 棵线段树和第 ⑤ 棵线段树拿出来。

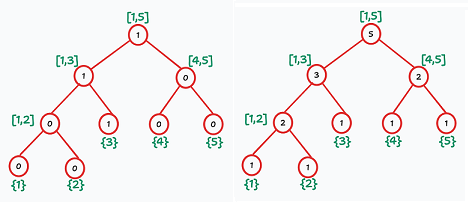
然后我们把对应节点的数相减，刚好就是 $[2, 5]$ 范围内数的个数。

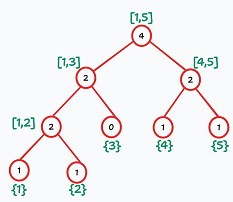
然后对于每一个区间 $[l, r]$ ，我们每次可以计算出 $[l, m i d]$ 范围内的数，如果数量 $\geq k$ ，就往左子树走，否则往右子树走；如果向右子树走，那么 $k$ 就变为 $k - l_{s u m}$ ， $l_{s u m}$ 表示左子树内数的数量。

由此模拟可得， $[2, 5]$ 中的第 $3$ 大的数为编号为 $4$ 的数，即 $26287$ 。

但是呢，我们不可能每到一个版本就建一颗完整的线段树，这样的话空间会爆炸，所以我们动态开点，每次建线段树只修改我们需要修改的节点，其他的节点我们仍然使用上一个版本的线段树的节点。举个例子：

假设我们现在是从第①棵线段树到第②棵线段树，我们发现我们只有蓝色的节点改变了数值，所以我们只添加这些改变数值的节点，其他节点仍然使用第①棵线段树的节点。

由此可以得出，我们不能单纯用 $p \times 2$ 和 $p \times 2 + 1$ 来代表一个节点的左右儿子节点，而是每一个节点都用一个特定的值来表示此节点，由此可以节省超大部分空间。具体如何实现可以去通过代码去理解。具体线段树开多少倍，建议往大里开，本人建议是 $N \times 40$ 左右。

代码实现

我们需要用动态开点的方法来储存每个节点的左右儿子编号，同时需要记录每一个历史版本的根节点。

离散化

 struct A{int w,id;}a[N];
bool cmp(A a,A b) {return a.w < b.w;}
void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i].w),a[i].id = i;
	sort(a + 1,a + n + 1,cmp);
	for(int i = 1;i <= n;i ++) _rank[a[i].id] = i,sum[i] = a[i].w;
}

建空树

 void build(int &p,int l,int r){
	p = ++tmp;
	if(l == r) return ;
	int mid = l + r >> 1;
	build(t[p].ls,l,mid);
	build(t[p].rs,mid + 1,r);
}
Set.build(rt[0],1,n);

加点

记录每一个线段树的根节点。

加点前我们先把历史版本复制过来，然后再进行修改，因为修改只会涉及其左子树或者其右子树。

通过查找当前加入得节点的位置，对其进行对应权值的修改。

 void new_copy(int &p) {t[++tmp] = t[p],p = tmp;}
void update(int &p,int l,int r,int x){
	new_copy(p),t[p].ans ++;
	if(l == r) return ;
	int mid = l + r >> 1;
	if(x <= mid) update(t[p].ls,l,mid,x);
	else update(t[p].rs,mid + 1,r,x); 
}
for(int i = 1;i <= n;i ++) rt[i] = rt[i - 1],Set.update(rt[i],1,n,_rank[i]);

查询

利用前缀和的思想，当前节点的权值 $=$ 版本 $r$ 当前节点的权值 $-$ 版本 $l - 1$ 当前节点的权值，如果左子树点的权值 $\leq k$ ，则往左子树查询，否则，向右子树查询， $k$ 变为 $k - l_{s u m}$ ， $l_{s u m}$ 表示左子树点的权值。

 int query(int a,int b,int l,int r,int x){
	if(l == r) return l;
	int l_sum = t[t[b].ls].ans - t[t[a].ls].ans;
	int mid = l + r >> 1;
	if(x <= l_sum) return query(t[a].ls,t[b].ls,l,mid,x);
	else return query(t[a].rs,t[b].rs,mid + 1,r,x - l_sum);
}
printf("%d\n",sum[Set.query(rt[l - 1],rt[r],1,n,x)]);

不得贪胜，不可不胜。

 #include <bits/stdc++.h>
#define N 200005
 
using namespace std;
 
int n,m,_rank[N],sum[N],tmp,rt[N];
 
struct A{int w,id;}a[N];
bool cmp(A a,A b) {return a.w < b.w;}
 
void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i].w),a[i].id = i;
	sort(a + 1,a + n + 1,cmp);
	for(int i = 1;i <= n;i ++) _rank[a[i].id] = i,sum[i] = a[i].w;
}
 
struct Set{
	struct Tree{int ls,rs,ans;}t[N << 5];
	
	void build(int &p,int l,int r){
		p = ++tmp;
		if(l == r) return ;
		int mid = l + r >> 1;
		build(t[p].ls,l,mid);
		build(t[p].rs,mid + 1,r);
	}
	
	void new_copy(int &p) {t[++tmp] = t[p],p = tmp;}
	
	void update(int &p,int l,int r,int x){
		new_copy(p),t[p].ans ++;
		if(l == r) return ;
		int mid = l + r >> 1;
		if(x <= mid) update(t[p].ls,l,mid,x);
		else update(t[p].rs,mid + 1,r,x); 
	}
	
	int query(int a,int b,int l,int r,int x){
		if(l == r) return l;
		int l_sum = t[t[b].ls].ans - t[t[a].ls].ans;
		int mid = l + r >> 1;
		if(x <= l_sum) return query(t[a].ls,t[b].ls,l,mid,x);
		else return query(t[a].rs,t[b].rs,mid + 1,r,x - l_sum);
	}
}Set;
 
void work(){
	Set.build(rt[0],1,n);
	for(int i = 1;i <= n;i ++) rt[i] = rt[i - 1],Set.update(rt[i],1,n,_rank[i]);
	int l,r,x;while(m --){
		scanf("%d%d%d",&l,&r,&x);
		printf("%d\n",sum[Set.query(rt[l - 1],rt[r],1,n,x)]);
	}
}
 
int main(){
	Input();
	work();
	return 0;
}

三倍经验： SP3946 MKTHNUM - K-th Number（代码完全一样）P1533 可怜的狗狗（改一下数组大小就行）。

习题

$1.$ P3919 【模板】可持久化线段树 1（可持久化数组）

线段树节点维护对应数组的值，然后利用主席树思想修改、查询即可。

若世有神明，亦会胜他半子。

 #include <bits/stdc++.h>
#define N 1000006
 
using namespace std;
 
int n,m,a[N],rt[N];
 
void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i]); 
}
 
struct Set_Tree{
	struct Tree{int ls,rs,ans;}t[N << 5];
	int tmp;
	
	void build(int &p,int l,int r){
		p = ++tmp;
		if(l == r) return (void)(t[p].ans = a[l]);
		int mid = l + r >> 1;
		build(t[p].ls,l,mid);
		build(t[p].rs,mid + 1,r);
	}
	
	void new_copy(int &p) {t[++tmp] = t[p],p = tmp;} 
	
	void update(int &p,int l,int r,int loc,int k){
		new_copy(p);
		if(l == r) return (void)(t[p].ans = k);
		int mid = l + r >> 1;
		if(loc <= mid) update(t[p].ls,l,mid,loc,k);
		else update(t[p].rs,mid + 1,r,loc,k);
	}
	
	int query(int p,int l,int r,int loc){
		if(l == r) return t[p].ans;
		int mid = l + r >> 1;
		if(loc <= mid) return query(t[p].ls,l,mid,loc);
		else return query(t[p].rs,mid + 1,r,loc);
	}
}Set;
 
void work(){
	Set.build(rt[0],1,n);
	int v,opt,loc,x;for(int i = 1;i <= m;i ++){
		scanf("%d%d%d",&v,&opt,&loc);
		rt[i] = rt[v];
		if(opt == 1) scanf("%d",&x),Set.update(rt[i],1,n,loc,x);
		if(opt == 2) printf("%d\n",Set.query(rt[v],1,n,loc));
	}
}
 
int main(){
	Input();
	work();
	return 0;
}

$2.$ P3567 [POI2014] KUR-Couriers

思路：对于序列 $a$ 依次加点，每一个线段树维护的是某一段连续的数内所有数出现的次数。查询时，每一个节点的值为 $t_{r_{a n s}} - t_{{l - 1}_{a n s}}$ 。从根节点开始，如果左子树（表示 $\leq m i d$ 的值）所有的数出现的次数 $\times 2 \leq r - l + 1$ ，则肯定不在左子树，同理右子树；若两边都不满足，证明没有，返回 $0$ 。

方寸棋盘，便是我的天地。

 #include <bits/stdc++.h>
#define N 500005
 
using namespace std;
 
int n,m,a[N],rt[N];
 
void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i]);
}
 
struct Set_Tree{
	struct Tree{int ls,rs,ans;}t[N << 5];
	int tmp;
	
	void build(int &p,int l,int r){
		p = ++tmp;t[p].ans = 0;
		if(l == r) return ;
		int mid = l + r >> 1;
		build(t[p].ls,l,mid);
		build(t[p].rs,mid + 1,r);
	}
	
	void new_copy(int &p) {t[++tmp] = t[p],p = tmp;}
	
	void update(int &p,int l,int r,int x){
		new_copy(p);t[p].ans ++;
		if(l == r) return ;
		int mid = l + r >> 1;
		if(x <= mid) update(t[p].ls,l,mid,x);
		else update(t[p].rs,mid + 1,r,x);
	}
	
	int query(int a,int b,int l,int r,int x){
		if(l == r) return l;
		int l_sum = t[t[a].ls].ans - t[t[b].ls].ans;
		int r_sum = t[t[a].rs].ans - t[t[b].rs].ans;
		int mid = l + r >> 1;
		if(l_sum * 2 > x) return query(t[a].ls,t[b].ls,l,mid,x);
		if(r_sum * 2 > x) return query(t[a].rs,t[b].rs,mid + 1,r,x);
		return 0;
	}
}Set;
 
void work(){
	Set.build(rt[0],1,n);
	for(int i = 1;i <= n;i ++) rt[i] = rt[i - 1],Set.update(rt[i],1,n,a[i]);
	int l,r;while(m --){
		scanf("%d%d",&l,&r);
		printf("%d\n",Set.query(rt[r],rt[l - 1],1,n,r - l + 1));
	}
}
 
int main(){
	Input();
	work();
	return 0;
}

$3.$ P1972 [SDOI2009] HH的项链

每一个线段树维护的是从 $1$ 到 $i$ 这个区间内每一段连续区间内出现的数的个数。当有重复的数字出现时，把这个数字上一次出现的位置对应线段树的所有区间内的 $a n s$ 减去 $1$ ，再把当前位置 $+ 1$ ，这样就保证了每个数字值记录一次，并且都是在相对靠后的位置记录的该数字，以方便查询。查询的时候，我们查询第 $r$ 个线段树，具体进行操作即可，具体查询方法请看代码。

双倍经验： SP3267 DQUERY - D-query（代码完全一样）。

黑子深邃，为长夜苍茫莫测；白子耀眼，若恒星亘古不变。

 #include <bits/stdc++.h>
#define N 1000006
 
using namespace std;
 
int n,m,a[N],rt[N],head[N];
 
void Input(){
	scanf("%d",&n);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i]);
}
 
struct Set_Tree{
	struct Tree{int ls,rs,ans;}t[N * 40];
	int tmp;
	
	void build(int &p,int l,int r){
		p = ++tmp;
		if(l == r) return ;
		int mid = l + r >> 1;
		build(t[p].ls,l,mid);
		build(t[p].rs,mid + 1,r);
	}
	
	void new_copy(int &p) {t[++tmp] = t[p],p = tmp;}
	
	void update(int &p,int l,int r,int loc,int x){
		new_copy(p);t[p].ans += x;
		if(l == r) return ;
		int mid = l + r >> 1;
		if(loc <= mid) update(t[p].ls,l,mid,loc,x);
		else update(t[p].rs,mid + 1,r,loc,x);
	}
	
	int query(int p,int l,int r,int x){
		if(l == r) return t[p].ans;
		int mid = l + r >> 1;
		if(x <= mid) return query(t[p].ls,l,mid,x) + t[t[p].rs].ans;
		else return query(t[p].rs,mid + 1,r,x);
	}
}Set;
 
void work(){
	Set.build(rt[0],1,n);
	for(int i = 1;i <= n;i ++){
		if(!head[a[i]]) rt[i] = rt[i - 1],Set.update(rt[i],1,n,i,1);
		else rt[i] = rt[i - 1],Set.update(rt[i],1,n,head[a[i]],-1),Set.update(rt[i],1,n,i,1);
		head[a[i]] = i;
	}
	int l,r;scanf("%d",&m);while(m --){
		scanf("%d%d",&l,&r);
		printf("%d\n",Set.query(rt[r],1,n,l));
	}
}
 
int main(){
	Input();
	work();
	return 0;
}

$4.$ P3939 数颜色

对于每一个颜色建一颗线段树，修改、查询即可。

会一直胜下去，为了父亲大人的认可。

 #include <bits/stdc++.h>
#define N 300005
 
using namespace std;
 
struct Set_Tree{
	struct Tree{int ls,rs,ans;}t[N * 40];
	int tmp;
	
	void update(int &p,int l,int r,int x,int k){
		if(!p) p = ++tmp;t[p].ans += k;
		if(l == r) return ;
		int mid = l + r >> 1;
		if(x <= mid) update(t[p].ls,l,mid,x,k);
		else update(t[p].rs,mid + 1,r,x,k);
	}
	
	int query(int p,int l,int r,int nl,int nr){
		if(nl <= l and r <= nr) return t[p].ans;
		int mid = l + r >> 1,res = 0;
		if(nl <= mid) res += query(t[p].ls,l,mid,nl,nr);
		if(nr > mid) res += query(t[p].rs,mid + 1,r,nl,nr);
		return res;
	}
}Set;
 
int n,m,a[N],rt[N];
 
void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i]),Set.update(rt[a[i]],1,n,i,1);
}
 
void work(){
	int opt,l,r,c;while(m --){
		scanf("%d",&opt);
		if(opt == 1) scanf("%d%d%d",&l,&r,&c),printf("%d\n",Set.query(rt[c],1,n,l,r));
		if(opt == 2) scanf("%d",&c),Set.update(rt[a[c]],1,n,c,-1),Set.update(rt[a[c]],1,n,c + 1,1),Set.update(rt[a[c + 1]],1,n,c + 1,-1),Set.update(rt[a[c + 1]],1,n,c,1),swap(a[c],a[c + 1]);
	}
}
 
int main(){
	Input();
	work();
	return 0;
}

$5.$ P2633 Count on a tree

前置知识：树链剖分。

这个题与模板不同的是，这个题的操作是在树上进行的。整体思路不变，只不过修改的时候是按照在熟练剖分预处理 $d f n$ 的时候依次修改，保存每一个历史版本，最后查询就是根据 $t_{u_{a n s}} + t_{v_{a n s}} - t_{l c a (u, v)_{a n s}} - t_{f a [l c a (u, v)]_{a n s}}$ 这一颗主席树去进行查询。

落子无悔。

 #include <bits/stdc++.h>
#define N 100005
 
using namespace std;
 
struct A{int w,id;}a[N];
bool cmp(A a,A b) {return a.w < b.w;}
 
struct Edge{int next,to;}edge[N << 1];
int head[N],cnt;
void add(int from,int to){
	edge[++cnt] = (Edge){head[from],to};
	head[from] = cnt;
}
 
 
int n,m,_rank[N],sum[N],rt[N],siz[N],dep[N],fa[N],top[N],son[N];
 
void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i].w),a[i].id = i;
	sort(a + 1,a + n + 1,cmp);
	for(int i = 1;i <= n;i ++) _rank[a[i].id] = i,sum[i] = a[i].w;
	for(int i = 1,u,v;i < n;i ++) scanf("%d%d",&u,&v),add(u,v),add(v,u);
}
 
struct Set_Tree{
	struct Set{int ls,rs,ans;}t[N * 40];
	int tmp;
	
	void build(int &p,int l,int r){
		p = ++tmp;t[p].ans = 0;
		if(l == r) return ;
		int mid = l + r >> 1;
		build(t[p].ls,l,mid);
		build(t[p].rs,mid + 1,r);
	}
	
	void new_copy(int &p) {t[++tmp] = t[p],p = tmp;}
	
	void update(int &p,int l,int r,int x){
		new_copy(p);
		if(l == r) return (void)(t[p].ans ++);
		int mid = l + r >> 1;
		if(x <= mid) update(t[p].ls,l,mid,x);
		else update(t[p].rs,mid + 1,r,x);
		t[p].ans = t[t[p].ls].ans + t[t[p].rs].ans;
	}
	
	int query(int x,int y,int w,int z,int l,int r,int k){
		if(l == r) return sum[l];
		int l_sum = t[t[x].ls].ans + t[t[y].ls].ans - t[t[w].ls].ans - t[t[z].ls].ans;
		int mid = l + r >> 1;
		if(k <= l_sum) return query(t[x].ls,t[y].ls,t[w].ls,t[z].ls,l,mid,k);
		else return query(t[x].rs,t[y].rs,t[w].rs,t[z].rs,mid + 1,r,k - l_sum);
	}
}Set;
 
struct Tree_apart{
	
	void dfs1(int x,int f,int deep){
		siz[x] = 1,dep[x] = deep,fa[x] = f;
		int maxnson = -1;
		for(int i = head[x];i;i = edge[i].next){
			int y = edge[i].to;
			if(y == f) continue;
			dfs1(y,x,deep + 1);
			siz[x] += siz[y];
			if(siz[y] > maxnson) maxnson = siz[y],son[x] = y;
		}
	}
	
	void dfs2(int x,int t){
		rt[x] = rt[fa[x]],Set.update(rt[x],1,n,_rank[x]);
		top[x] = t;
		if(!son[x]) return ;
		dfs2(son[x],t);
		for(int i = head[x];i;i = edge[i].next){
			int y = edge[i].to;
			if(y == son[x] or y == fa[x]) continue;
			dfs2(y,y);
		}
	}	
	
	int LCA(int x,int y){
		while(top[x] != top[y]){
			if(dep[top[x]] < dep[top[y]]) swap(x,y);
			x = fa[top[x]];
		}
		return dep[x] < dep[y] ? x : y;
	}
}Ta;
 
void work(){
	Ta.dfs1(1,0,1),Set.build(rt[0],1,n),Ta.dfs2(1,1);
	int u,v,k,lst = 0;while(m --){
		scanf("%d%d%d",&u,&v,&k);u ^= lst;
		int l = Ta.LCA(u,v);
		lst = Set.query(rt[u],rt[v],rt[l],rt[fa[l]],1,n,k);
		printf("%d\n",lst);
	}
}
 
int main(){
	Input();
	work();
	return 0;
}

$6.$ P1383 高级打字机

每一个线段树就维护每个节点是哪一个字母就行。对于第一个操作，就在第一个还没有插入字母的位置插入即可，具体实现方法就是，维护一个 $n u m$ 值，表示区间内一共插入了多少字母，就可以方便找到第一个没有插入字母的位置，可以见代码。对于第二个操作，之间令根节点等于那一个线段树版本的根节点即可。查询就不用多说了。

点击查看代码

 #include <bits/stdc++.h>
#define N 100005
 
using namespace std;
 
struct Set_Tree{
	struct Tree{int ls,rs,ans,sum;}t[N << 5];
	int tmp;
	
	void build(int &p,int l,int r){
		p = ++tmp;t[p].sum = 0;
		if(l == r) return ;
		int mid = l + r >> 1;
		build(t[p].ls,l,mid);
		build(t[p].rs,mid + 1,r);
	}
	
	void new_copy(int &p) {t[++tmp] = t[p],p = tmp;}
	
	void update(int &p,int l,int r,char x){
		new_copy(p);t[p].sum ++;
		if(l == r) return (void)(t[p].ans = x);
		int mid = l + r >> 1;
		if(t[t[p].ls].sum < mid - l + 1) update(t[p].ls,l,mid,x);
		else update(t[p].rs,mid + 1,r,x);
	}
	
	char query(int p,int l,int r,int k){
		if(l == r) return t[p].ans;
		int mid = l + r >> 1;
		if(t[t[p].ls].sum >= k) return query(t[p].ls,l,mid,k);
		else return query(t[p].rs,mid + 1,r,k - t[t[p].ls].sum);
	}
}Set;
 
int n,rt[N];
 
int main(){
	scanf("%d",&n);Set.build(rt[0],1,n);
	char opt,c;int x,ans = 0;for(int i = 1;i <= n;i ++){
		cin >> opt;
		if(opt == 'T') cin >> c,ans ++,rt[ans] = rt[ans - 1],Set.update(rt[ans],1,n,c);
		if(opt == 'U') scanf("%d",&x),ans ++,rt[ans] = rt[ans - x - 1];
		if(opt == 'Q') scanf("%d",&x),cout << Set.query(rt[ans],1,n,x) << endl;
	}
	return 0;
}

上一篇乘法逆元

下一篇基础优化技巧1

posted @ 2023-11-02 18:10 Joy_Dream_Glory 阅读(38) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 基础优化技巧1

· 分块与莫队

· 可持久化线段树小记

· 可持久化线段树/并查集

· #5. 可持久化线段树

阅读排行：
· winform 绘制太阳，地球，月球运作规律
· TypeScript + Deepseek 打造卜卦网站：技术与玄学的结合
· AI 智能体引爆开源社区「GitHub 热点速览」
· Manus的开源复刻OpenManus初探
· 写一个简单的SQL生成工具

Joy_Dream_Glory

可持久化线段树

前置

引入

解释

思路

代码实现

离散化

建空树

加点

查询

习题

$1.$ P3919 【模板】可持久化线段树 1（可持久化数组）

$2.$ P3567 [POI2014] KUR-Couriers

$3.$ P1972 [SDOI2009] HH的项链

$4.$ P3939 数颜色

$5.$ P2633 Count on a tree

$6.$ P1383 高级打字机

公告

常用链接

随笔分类

随笔档案

	struct A{int w,id;}a[N];
	bool cmp(A a,A b) {return a.w < b.w;}
	void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i].w),a[i].id = i;
	sort(a + 1,a + n + 1,cmp);
	for(int i = 1;i <= n;i ++) _rank[a[i].id] = i,sum[i] = a[i].w;
	}

	void build(int &p,int l,int r){
	p = ++tmp;
	if(l == r) return ;
	int mid = l + r >> 1;
	build(t[p].ls,l,mid);
	build(t[p].rs,mid + 1,r);
	}
	Set.build(rt[0],1,n);

	void new_copy(int &p) {t[++tmp] = t[p],p = tmp;}
	void update(int &p,int l,int r,int x){
	new_copy(p),t[p].ans ++;
	if(l == r) return ;
	int mid = l + r >> 1;
	if(x <= mid) update(t[p].ls,l,mid,x);
	else update(t[p].rs,mid + 1,r,x);
	}
	for(int i = 1;i <= n;i ++) rt[i] = rt[i - 1],Set.update(rt[i],1,n,_rank[i]);

	int query(int a,int b,int l,int r,int x){
	if(l == r) return l;
	int l_sum = t[t[b].ls].ans - t[t[a].ls].ans;
	int mid = l + r >> 1;
	if(x <= l_sum) return query(t[a].ls,t[b].ls,l,mid,x);
	else return query(t[a].rs,t[b].rs,mid + 1,r,x - l_sum);
	}
	printf("%d\n",sum[Set.query(rt[l - 1],rt[r],1,n,x)]);

	#include <bits/stdc++.h>
	#define N 200005

	using namespace std;

	int n,m,_rank[N],sum[N],tmp,rt[N];

	struct A{int w,id;}a[N];
	bool cmp(A a,A b) {return a.w < b.w;}

	void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i].w),a[i].id = i;
	sort(a + 1,a + n + 1,cmp);
	for(int i = 1;i <= n;i ++) _rank[a[i].id] = i,sum[i] = a[i].w;
	}

	struct Set{
	struct Tree{int ls,rs,ans;}t[N << 5];

	void build(int &p,int l,int r){
	p = ++tmp;
	if(l == r) return ;
	int mid = l + r >> 1;
	build(t[p].ls,l,mid);
	build(t[p].rs,mid + 1,r);
	}

	void new_copy(int &p) {t[++tmp] = t[p],p = tmp;}

	void update(int &p,int l,int r,int x){
	new_copy(p),t[p].ans ++;
	if(l == r) return ;
	int mid = l + r >> 1;
	if(x <= mid) update(t[p].ls,l,mid,x);
	else update(t[p].rs,mid + 1,r,x);
	}

	int query(int a,int b,int l,int r,int x){
	if(l == r) return l;
	int l_sum = t[t[b].ls].ans - t[t[a].ls].ans;
	int mid = l + r >> 1;
	if(x <= l_sum) return query(t[a].ls,t[b].ls,l,mid,x);
	else return query(t[a].rs,t[b].rs,mid + 1,r,x - l_sum);
	}
	}Set;

	void work(){
	Set.build(rt[0],1,n);
	for(int i = 1;i <= n;i ++) rt[i] = rt[i - 1],Set.update(rt[i],1,n,_rank[i]);
	int l,r,x;while(m --){
	scanf("%d%d%d",&l,&r,&x);
	printf("%d\n",sum[Set.query(rt[l - 1],rt[r],1,n,x)]);
	}
	}

	int main(){
	Input();
	work();
	return 0;
	}

	#include <bits/stdc++.h>
	#define N 1000006

	using namespace std;

	int n,m,a[N],rt[N];

	void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i]);
	}

	struct Set_Tree{
	struct Tree{int ls,rs,ans;}t[N << 5];
	int tmp;

	void build(int &p,int l,int r){
	p = ++tmp;
	if(l == r) return (void)(t[p].ans = a[l]);
	int mid = l + r >> 1;
	build(t[p].ls,l,mid);
	build(t[p].rs,mid + 1,r);
	}

	void new_copy(int &p) {t[++tmp] = t[p],p = tmp;}

	void update(int &p,int l,int r,int loc,int k){
	new_copy(p);
	if(l == r) return (void)(t[p].ans = k);
	int mid = l + r >> 1;
	if(loc <= mid) update(t[p].ls,l,mid,loc,k);
	else update(t[p].rs,mid + 1,r,loc,k);
	}

	int query(int p,int l,int r,int loc){
	if(l == r) return t[p].ans;
	int mid = l + r >> 1;
	if(loc <= mid) return query(t[p].ls,l,mid,loc);
	else return query(t[p].rs,mid + 1,r,loc);
	}
	}Set;

	void work(){
	Set.build(rt[0],1,n);
	int v,opt,loc,x;for(int i = 1;i <= m;i ++){
	scanf("%d%d%d",&v,&opt,&loc);
	rt[i] = rt[v];
	if(opt == 1) scanf("%d",&x),Set.update(rt[i],1,n,loc,x);
	if(opt == 2) printf("%d\n",Set.query(rt[v],1,n,loc));
	}
	}

	int main(){
	Input();
	work();
	return 0;
	}

	#include <bits/stdc++.h>
	#define N 500005

	using namespace std;

	int n,m,a[N],rt[N];

	void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i]);
	}

	struct Set_Tree{
	struct Tree{int ls,rs,ans;}t[N << 5];
	int tmp;

	void build(int &p,int l,int r){
	p = ++tmp;t[p].ans = 0;
	if(l == r) return ;
	int mid = l + r >> 1;
	build(t[p].ls,l,mid);
	build(t[p].rs,mid + 1,r);
	}

	void new_copy(int &p) {t[++tmp] = t[p],p = tmp;}

	void update(int &p,int l,int r,int x){
	new_copy(p);t[p].ans ++;
	if(l == r) return ;
	int mid = l + r >> 1;
	if(x <= mid) update(t[p].ls,l,mid,x);
	else update(t[p].rs,mid + 1,r,x);
	}

	int query(int a,int b,int l,int r,int x){
	if(l == r) return l;
	int l_sum = t[t[a].ls].ans - t[t[b].ls].ans;
	int r_sum = t[t[a].rs].ans - t[t[b].rs].ans;
	int mid = l + r >> 1;
	if(l_sum * 2 > x) return query(t[a].ls,t[b].ls,l,mid,x);
	if(r_sum * 2 > x) return query(t[a].rs,t[b].rs,mid + 1,r,x);
	return 0;
	}
	}Set;

	void work(){
	Set.build(rt[0],1,n);
	for(int i = 1;i <= n;i ++) rt[i] = rt[i - 1],Set.update(rt[i],1,n,a[i]);
	int l,r;while(m --){
	scanf("%d%d",&l,&r);
	printf("%d\n",Set.query(rt[r],rt[l - 1],1,n,r - l + 1));
	}
	}

	int main(){
	Input();
	work();
	return 0;
	}

	#include <bits/stdc++.h>
	#define N 300005

	using namespace std;

	struct Set_Tree{
	struct Tree{int ls,rs,ans;}t[N * 40];
	int tmp;

	void update(int &p,int l,int r,int x,int k){
	if(!p) p = ++tmp;t[p].ans += k;
	if(l == r) return ;
	int mid = l + r >> 1;
	if(x <= mid) update(t[p].ls,l,mid,x,k);
	else update(t[p].rs,mid + 1,r,x,k);
	}

	int query(int p,int l,int r,int nl,int nr){
	if(nl <= l and r <= nr) return t[p].ans;
	int mid = l + r >> 1,res = 0;
	if(nl <= mid) res += query(t[p].ls,l,mid,nl,nr);
	if(nr > mid) res += query(t[p].rs,mid + 1,r,nl,nr);
	return res;
	}
	}Set;

	int n,m,a[N],rt[N];

	void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i]),Set.update(rt[a[i]],1,n,i,1);
	}

	void work(){
	int opt,l,r,c;while(m --){
	scanf("%d",&opt);
	if(opt == 1) scanf("%d%d%d",&l,&r,&c),printf("%d\n",Set.query(rt[c],1,n,l,r));
	if(opt == 2) scanf("%d",&c),Set.update(rt[a[c]],1,n,c,-1),Set.update(rt[a[c]],1,n,c + 1,1),Set.update(rt[a[c + 1]],1,n,c + 1,-1),Set.update(rt[a[c + 1]],1,n,c,1),swap(a[c],a[c + 1]);
	}
	}

	int main(){
	Input();
	work();
	return 0;
	}

	#include <bits/stdc++.h>
	#define N 100005

	using namespace std;

	struct A{int w,id;}a[N];
	bool cmp(A a,A b) {return a.w < b.w;}

	struct Edge{int next,to;}edge[N << 1];
	int head[N],cnt;
	void add(int from,int to){
	edge[++cnt] = (Edge){head[from],to};
	head[from] = cnt;
	}


	int n,m,_rank[N],sum[N],rt[N],siz[N],dep[N],fa[N],top[N],son[N];

	void Input(){
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i].w),a[i].id = i;
	sort(a + 1,a + n + 1,cmp);
	for(int i = 1;i <= n;i ++) _rank[a[i].id] = i,sum[i] = a[i].w;
	for(int i = 1,u,v;i < n;i ++) scanf("%d%d",&u,&v),add(u,v),add(v,u);
	}

	struct Set_Tree{
	struct Set{int ls,rs,ans;}t[N * 40];
	int tmp;

	void build(int &p,int l,int r){
	p = ++tmp;t[p].ans = 0;
	if(l == r) return ;
	int mid = l + r >> 1;
	build(t[p].ls,l,mid);
	build(t[p].rs,mid + 1,r);
	}

	void new_copy(int &p) {t[++tmp] = t[p],p = tmp;}

	void update(int &p,int l,int r,int x){
	new_copy(p);
	if(l == r) return (void)(t[p].ans ++);
	int mid = l + r >> 1;
	if(x <= mid) update(t[p].ls,l,mid,x);
	else update(t[p].rs,mid + 1,r,x);
	t[p].ans = t[t[p].ls].ans + t[t[p].rs].ans;
	}

	int query(int x,int y,int w,int z,int l,int r,int k){
	if(l == r) return sum[l];
	int l_sum = t[t[x].ls].ans + t[t[y].ls].ans - t[t[w].ls].ans - t[t[z].ls].ans;
	int mid = l + r >> 1;
	if(k <= l_sum) return query(t[x].ls,t[y].ls,t[w].ls,t[z].ls,l,mid,k);
	else return query(t[x].rs,t[y].rs,t[w].rs,t[z].rs,mid + 1,r,k - l_sum);
	}
	}Set;

	struct Tree_apart{

	void dfs1(int x,int f,int deep){
	siz[x] = 1,dep[x] = deep,fa[x] = f;
	int maxnson = -1;
	for(int i = head[x];i;i = edge[i].next){
	int y = edge[i].to;
	if(y == f) continue;
	dfs1(y,x,deep + 1);
	siz[x] += siz[y];
	if(siz[y] > maxnson) maxnson = siz[y],son[x] = y;
	}
	}

	void dfs2(int x,int t){
	rt[x] = rt[fa[x]],Set.update(rt[x],1,n,_rank[x]);
	top[x] = t;
	if(!son[x]) return ;
	dfs2(son[x],t);
	for(int i = head[x];i;i = edge[i].next){
	int y = edge[i].to;
	if(y == son[x] or y == fa[x]) continue;
	dfs2(y,y);
	}
	}

	int LCA(int x,int y){
	while(top[x] != top[y]){
	if(dep[top[x]] < dep[top[y]]) swap(x,y);
	x = fa[top[x]];
	}
	return dep[x] < dep[y] ? x : y;
	}
	}Ta;

	void work(){
	Ta.dfs1(1,0,1),Set.build(rt[0],1,n),Ta.dfs2(1,1);
	int u,v,k,lst = 0;while(m --){
	scanf("%d%d%d",&u,&v,&k);u ^= lst;
	int l = Ta.LCA(u,v);
	lst = Set.query(rt[u],rt[v],rt[l],rt[fa[l]],1,n,k);
	printf("%d\n",lst);
	}
	}

	int main(){
	Input();
	work();
	return 0;
	}

Joy_Dream_Glory

可持久化线段树

前置

引入

解释

思路

代码实现

离散化

建空树

加点

查询

习题

1. P3919 【模板】可持久化线段树 1（可持久化数组）

2. P3567 [POI2014] KUR-Couriers

3. P1972 [SDOI2009] HH的项链

4. P3939 数颜色

5. P2633 Count on a tree

6. P1383 高级打字机

公告

常用链接

随笔分类

随笔档案

$1.$ P3919 【模板】可持久化线段树 1（可持久化数组）

$2.$ P3567 [POI2014] KUR-Couriers

$3.$ P1972 [SDOI2009] HH的项链

$4.$ P3939 数颜色

$5.$ P2633 Count on a tree

$6.$ P1383 高级打字机