(180905)如何通过梯度下降法降低损失----Google机器学习速成课程笔记
以下内容只需了解,理解更好;像梯度下降法这些机器学习算法都已经被机器学习框架所集成了,只要会用就好
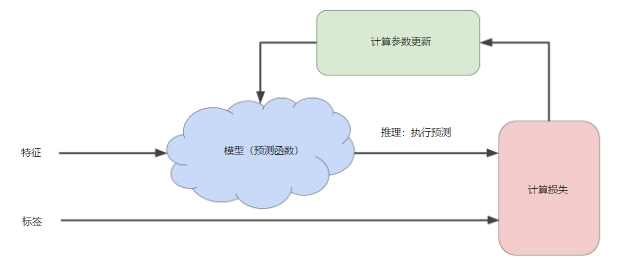
通过迭代减少损失
如图所示,机器学习算法通过不断地通过模型得出预测值,再检验损失进而调整模型的参数(使得损失更小的参数)更新模型,直到损失尽可能不再变化或至少变化极其缓慢为止为止
计算损失的部分通过损失函数,一般就是平方损失函数
这里的迭代和编程语言中的稍有不同,它主要强调的是按照同一步骤,次数多而已
如下将介绍一种降低损失的方法:梯度下降法
梯度下降法
- 了解:深入浅出–梯度下降法及其实现,想深入了解最好仔细想想这篇文章
- 梯度是偏导数,对于多元变量而言是一个矢量值
上面博客中的图片,J 是多元 θ 的函数,梯度就是对多个变量分别求导,如图

- 为了求得损失值最小值,应该向梯度下降的方向前进,且最小值就是在梯度趋近与0的地方取得(损失函数收敛处)
- 起始点θ0可以随便取,下一个点θ1由公式可求得
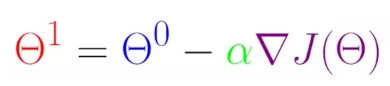
α 是学习速率,也叫做步长;梯度取负值表示向下降最快的方向前进
个人对减小损失的理解
这里在谈谈我的理解,结合上面训练模型的流程,通过梯度下降法可以得出损失的最小值和取得最小值之处的一组权重值 <θ0、θ1、θ2…> (因为梯度是权重的函数,梯度趋近 0【这里0也应该是矢量值】 时所得到的 θ 就是所求权重,再结合损失值可得到偏差)
而样本不同,训练的批次不同,可以求出若干组这样的值。只要选取使得损失最小且趋于稳定那一组参数就能构成理想的模型
理想的步长 α
明确步长过短运算量太大,降低效率;过长,可能永远取不到最小值
每个回归问题都存在一个金发姑娘学习速率。“金发姑娘”值与损失函数的平坦程度相关。如果您知道损失函数的梯度较小,则可以放心地试着采用更大的学习速率,以补偿较小的梯度并获得更大的步长。
理想的学习速率:
一维空间(一元变量)中的理想学习速率是 1/f(x)″
二维或多维空间(多元变量)中的理想学习速率是海森矩阵(由二阶偏导数组成的矩阵)的倒数
广义凸函数的情况则更为复杂。
随机梯度下降法(SGD)
- 批量:单次迭代过程中用于求梯度下降法的样本总数
- 对于样本非常大的情况,批量越大,花的时间就越多,而且出现数据冗杂的情况越高
- SGD:从数据集中随机选择1个样本,迭代次数足够多,可以通过小得多的数据集估算(尽管过程非常杂乱)出较大的平均值
随机梯度下降法 (SGD) 将这种想法运用到极致,它每次迭代只使用一个样本(批量大小为 1)。如果进行足够的迭代,SGD 也可以发挥作用,但过程会非常杂乱。“随机”这一术语表示构成各个批量的一个样本都是随机选择的
小批量随机梯度下降法(小批量 SGD)
通常随机选取10~1000个样本,介于全批量梯度下降和随机梯度下降法之间。 可以减少 SGD 中的杂乱样本数量,但仍然比全批量更高效