实验一拓展文献阅读—反向传播计算图上的微积分

 

 

 

 

 

http://colah.github.io/posts/2015-08-Backprop/?spm=a2c4e.11153940.blogcont149583.20.4ab360c05me4Uv

Calculus on Computational Graphs: Backpropagation

计算图上的微积分：反向传播

Introduction

反向传播是使训练深度模型在计算上易于处理的关键算法。对于现代神经网络，相对于天真的实现，它可以使梯度下降训练的速度提高一千万倍。这是一个模型需要一周的培训和20万年的差异。

除了在深度学习中的应用之外，反向传播是许多其他领域的强大计算工具，从天气预报到分析数值稳定性 - 它只是用不同的名称。实际上，该算法在不同领域至少被重新发明了几十次（参见Griewank（2010））。一般的，独立于应用程序，名称是“反向模式区分”。

从根本上说，它是一种快速计算衍生品的技术。这是一个必不可少的技巧，不仅在深度学习中，而且在各种数值计算环境中。

计算图

计算图是思考数学表达式的好方法。 例如，考虑表达式e =（a + b）*（b + 1）。 有三个操作：两个加法和一个乘法。 为了帮助我们讨论这个问题，让我们介绍两个中间变量c和d，以便每个函数的输出都有一个变量。 我们现在有：

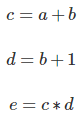
为了创建计算图，我们将这些操作以及输入变量中的每一个都放入节点中。 当一个节点的值是另一个节点的输入时，箭头从一个节点到另一个节点。

这些类型的图表一直出现在计算机科学中，特别是在谈论功能程序时。 它们与依赖图和调用图的概念密切相关。 它们也是流行的深度学习框架Theano背后的核心抽象。

我们可以通过将输入变量设置为特定值并通过图形向上计算节点来评估表达式。 例如，设置a = 2且b = 1：

 

表达式的计算结果为6。

计算图的导数

如果想要理解计算图中的导数，关键是理解边缘上的导数。 如果a直接影响c，那么我们想知道它如何影响c。 如果a发生了一点变化，c会如何变化？ 我们称之为c的偏导数。

要评估此图中的偏导数，我们需要求“和法则”和“乘积法则”：

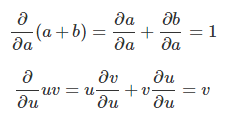
下面，图表标记了每条边上的导数。

 

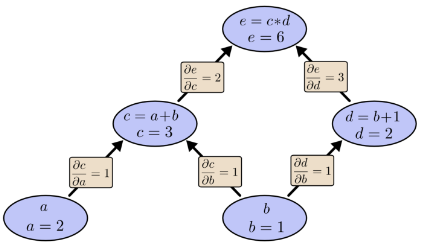
如果我们想了解非直接连接的节点如何相互影响，该怎么办？ 让我们考虑一下如何影响e。 如果我们以1的速度改变a，则c也以1的速度变化。反过来，c以1的速度变化导致e以2的速度变化。因此，e关于a以1 * 2的速率变化。

一般规则是将从一个节点到另一个节点的所有可能路径相加，将路径的每个边缘上的导数相乘。 例如，为了得到关于b的e的导数，我们得到：

 

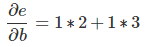
这解释了b如何影响e到c以及它如何通过d影响它。

这种一般的“路径总和”规则只是思考多变量链规则的另一种方式。

因子分解路径

仅仅“对路径求和”的问题在于，很容易在可能路径的数量上发生组合爆炸。

 

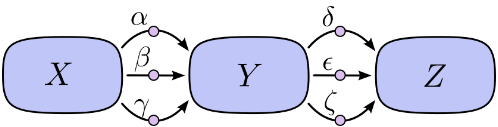
 在上图中，从X到Y有三条路径，从Y到Z有另外三条路径。 如果我们想通过对所有路径求和得到导数∂Z/∂X，我们需要求和3 * 3 = 9路径：

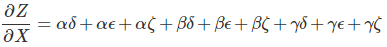
上面只有九条路径，但随着图形变得越来越复杂，路径的数量会呈指数增长。

不要只是天真地对路径求和，而是将它们考虑起来要好得多：

这就是“前向模式差分”和“反向模式差分”的用武之地。它们是通过分解路径来有效计算总和的算法。 它们不是明确地对所有路径求和，而是通过在每个节点处将路径合并在一起来更有效地计算相同的和。 实际上，两种算法都只触摸每个边缘一次！

前向模式差分从图形的输入开始并向末尾移动。 在每个节点处，它对所有进入的路径求和。每个路径代表输入影响该节点的一种方式。 通过将它们相加，我们得到节点受输入影响的总方式，即为导数。

 

虽然可能没有从图形方面考虑它，但是前向模式差分非常类似于在介绍微积分类时隐含学习的内容。

另一方面，反向模式差分从图形的输出开始并向开始移动。 在每个节点处，它合并源自该节点的所有路径。

 

 前向模式差分跟踪一个输入如何影响每个节点。 反向模式差分跟踪每个节点如何影响一个输出。 也就是说，前向模式差分将运算符∂/∂X应用于每个节点，而反向模式差分将运算符∂Z/∂应用于每个节点。

计算的收益（成功之处）victories

此时，您可能想知道为什么有人会关心反向模式差分。 它看起来像是一种与前向模式做同样事情的奇怪方式。 有一些优势吗？

让我们再考虑一下我们原来的例子：

 

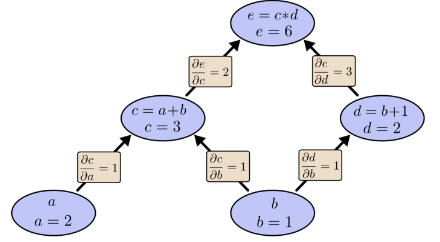
 我们可以使用从b出发的前向模式差分。 关于b的每个节点的导数如下图：

我们计算了∂e/∂b，它是我们输出相对于我们的一个输入的导数。

如果我们从e向下进行反向模式差分怎么办？ 这给了我们关于每个节点的e的导数：

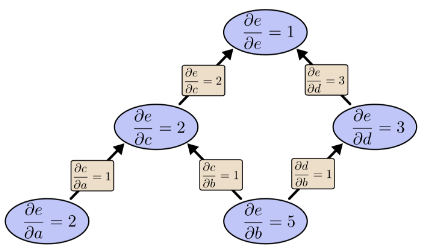
反向模式区分为我们提供了关于每个节点的e的导数时，注意是每个节点。我们得到∂e/∂a和∂e/∂b，e相对于两个输入的导数。前向模式微分给出了我们输出相对于单个输入的导数，但是反向模式微分给了我们全部。

对于此图表，这只是两倍加速的因子，但想象一下具有一百万个输入和一个输出的功能。前向模式的区分需要我们通过图表一百万次来获得乘积。反向模式微分可以一举得到它们！加速百万分之一是非常好的！

在训练神经网络时，我们考虑成本（描述神经网络执行有多糟糕的值）作为参数的函数（描述网络行为的数字）。我们想要计算所有参数的成本导数，用于梯度下降。现在，神经网络中通常有数百万甚至数千万个参数。因此，在神经网络环境中称为反向传播的反向模式微分给我们带来了巨大的加速！

（在任何情况下，前向模式区分更有意义吗？是的，有！反向模式给出了一个输出相对于所有输入的导数，前向模式给出了所有输出相对于一个输入。如果一个具有大量输出的功能，前向模式区分可以更快，更快。）

这不是微不足道的吗？

当我第一次明白反向传播是什么时，我的反应是：“哦，那只是连锁规则！我们怎么花这么长时间才弄明白？“我不是唯一一个有这种反应的人。确实，如果你问“有没有一种聪明的方法来计算前馈神经网络中的导数？”答案并不那么困难。

但我认为这比看起来要困难得多。你看，在反传播发明的时候，人们并没有把注意力集中在我们研究的前馈神经网络上。微分是训练它们的正确方法，这一点也不明显。一旦你意识到你可以快速计算微分时，这些只是显而易见的存在循环依赖。

更糟糕的是，在随意的思想中，将任何循环依赖关系都写下来是很容易的。用衍生物训练神经网络？当然，你只是陷入局部极小。显然，计算所有这些微分会很昂贵。这只是因为我们知道这种方法有效，我们不会立即开始列出它可能没有的原因。

这是后见之明的好处。一旦你构思了问题，最艰难的工作就已经完成了。

结论

微分比你想象的要容易。这是从这篇文章中拿走的主要教训。事实上，它们的价格非常便宜，而我们愚蠢的人类不得不反复重新发现这一事实。在深度学习中要理解这一点很重要。在其他领域中了解它也是一件非常有用的事情，如果不是常识，那就更是如此。

还有其他课程吗？我觉得有。

反向传播也是理解微分如何流经模型的有用透镜。这对于推理某些模型难以优化的原因非常有用。这方面的典型例子是递归神经网络中逐渐消失的梯度问题。

最后，我声称有一个广泛的算法课程可以从这些技术中剔除。反向传播和前向模式区分使用一对强大的技巧（线性化和动态编程）来比计算可能的更有效地计算导数。如果您真的了解这些技术，您可以使用它们来有效地计算涉及衍生物的其他几个有趣的表达式。

这篇文章给出了非常抽象的反向传播处理方法。我强烈建议阅读Michael Nielsen关于它的章节进行精彩讨论，更具体地关注神经网络。