OO前三次作业思考（第一次OO——Blog）

OO前三次作业总结

基于度量分析程序结构

由于三次作业较多，决定分析内容、功能最为复杂的第三次作业。

 

上图为第三次作业的类图。我使用了一个抽象类Factor，写了五个因子继承Factor，然后又单独开了一个Term类，还有表达式类，其中Expression因子包含一个表达式类，其他就是常见的Main类，InputHandle类，求导和输出都在Main类中完成。个人认为本次的架构还可以，较为清晰，具有延展性，若是加入其他因子只需要继续继承Factor类，而在其他类中改动无需太多就可继续使用，而在递归求导方面，每一个类都有一个Derivation方法，递归下降进行求导。

 

 

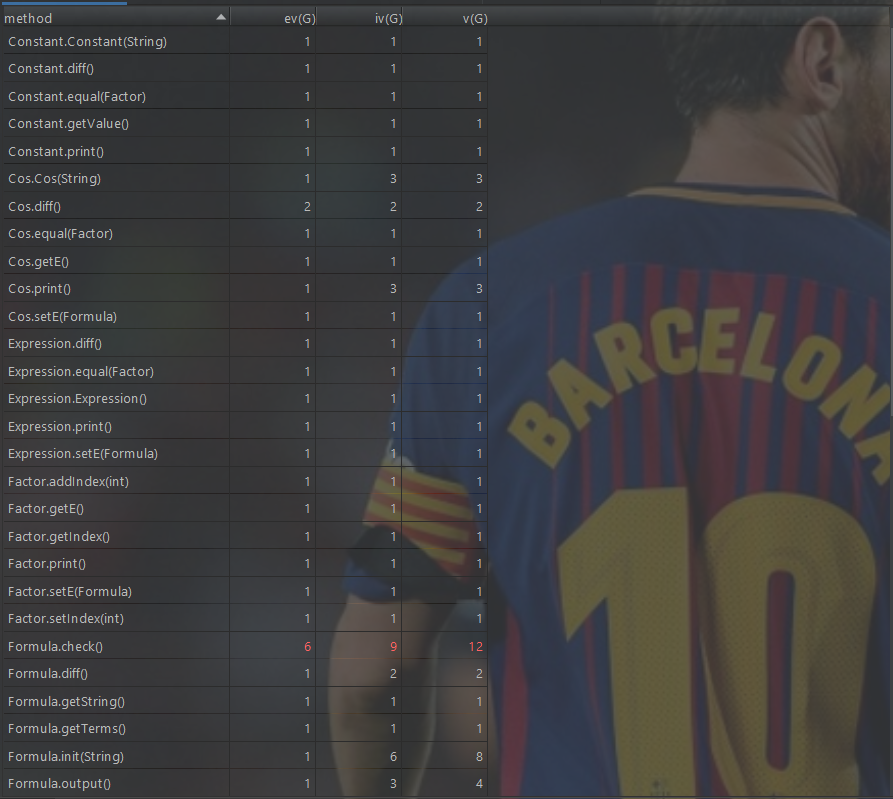
以上两张图为MetricsReloaded对于代码复杂度在方法层面的分析，可以看出基本复杂度，结构最复杂的方法集中在了初始化，判断输入合法性这两个方面，因为我的输入合法性判断采取大量的正则表达式以及递归判断，导致复杂也可以理解，并没有想到很好的解决合法性判断的方法。

 

 

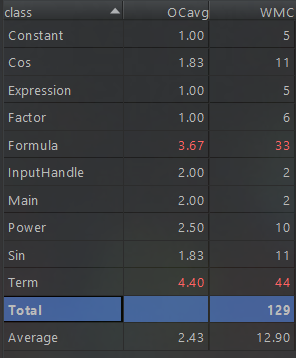
上图为类复杂度的分析，可以看出复杂度高的类为Formula类和Term类，这两个类包含了大量的正则判断，即合法性判断，还有通过matcher.group方法获取输入内容，导致复杂度过高。

 

分析⾃⼰程序的bug

前两次作业我的鲁棒性较好，并没有被互测或是公测用例发现bug，但是第三次作业出现了bug，公测阶段还好，并没有出太多极端数据，而在互测阶段，发现了bug，说起来导致bug的原因很简单，在我的Constant类中，使用了int来存储常数项的值，而不是BigInteger，但是在指导书中明确说明了带符号整数，同时提示中也给出了BigInteger选项，但是我在码代码的时候习惯性的使用了int类型，且在自己测试的时候并没有进行覆盖性测试，导致了这个点遭到遗漏，现在想来是因为以往使用int类型次数过多，在定义一个变量且是数值是，会习惯性的使用int类型，还并没有完全适应Java的编程习惯，这一点在日后的编程过程中会多多注意。（同时有一点，在互测阶段有一个同学hack了我这个bug三次，且使用的是显然可以看出的手造数据，而不是自动生成的数据，显然是明知同质bug而hack。。。。就很让人不舒服，唉）

同时我发现，在写代码初期，逐步测试是个非常好的习惯，每写出一个功能，就通过toString方法进行检测，数据复杂程度无需太大，就可以发现自己写出的许多bug，这样每一步都会修改前一步的bug，大大减少了后期程序成型后修复bug的时间，且前期代码数较少，也方便进行修复。

 

分析⾃⼰发现别⼈程序bug所采⽤的策略

在互测阶段，第一次作业我还是采取了极其低效的打开了8个IDEA窗口，对于8份代码逐个调试，速度极其缓慢，且测试样例的覆盖面极低，基本是根据自己对于指导书的理解，给出一些包含可能坑点的测试样例，还有就是在和同学交流中，得到的一些出错率较高的样例。但是在第一次作业的问题上，由于代码架构并不复杂，还存在读代码找bug的可能，比如阅读正则表达式，查看是否有漏判或是误判的可能。而之后的代码，复杂程度太高，架构不同可能导致代码量的急剧增大，阅读代码找bug会有巨大的工作量，而我并没有太多时间。。。

第二次以及第三次作业中，我从网上学习了一些自动化测试的方法，同时在同学的帮助写，写了一个低配版的评测机，使用python的xeger，通过正则表达式生成符合指导书要求的测试样例，并且使用python调用所有的.class文件，进行测试，python调用java的方法是参考了讨论区大佬进行的分享，在自动化评测机制的帮助下，评测效率提高了，那天晚上我就跑了2w+测试数据，有所收获，但是对于跑出的样例，由于是自动生成，导致我并不了解这份代码导致WA或是WF的原因，也就无法很好的区分是否同质bug，导致在提交bug时，并不能保证不是同质bug，也无法很好的加强自己的代码能力。

第三次作业同样如此，但由于嵌套因子的存在，导致无法正则生成测试样例，而采用了C语言，随机生成样例，但这次并没有测试出太多的WF或是WA，而之后我才查看ROOM内其他的hack样例时，发现了一些极其简单的测试数据，但就是由于其简单，导致生成数据时可能生成的概率极低，而若是我个人手写生成样例，存在可能性去覆盖这些点，因此我对于自动评测机感觉，有利有弊，打算今后的测试以个人手动测试为主，其他时间保持评测机运行即可。

 

Applying Creational Pattern

我的架构并不是很成功，三次作业，三次重构，能够沿用的怕是只有InputHandle类，过于真实。首先第一次写Java作业的时候，根本没想到复用性的问题，大量的面向过程编程思想，导致我只是使用了三个类，没有任何的面向对象。而第二次作业，当时为了保证程序的正确性，并没有胆量去使用递归求导的方法，于是在明知第三次作业可能有嵌套因子的情况下，我选择了使用公式求导，毕竟当时只有三角函数以及带常系数的幂函数，求导公式并不复杂，复用性极差但成功的保证了在强侧以及互测阶段没有被找出bug，也算一种另类的优势吧。

但第三次作业就不一样了，没有一个好的架构甚至无法完成对于数据合法性的判断，最初的架构花去了我大量的时间，写代码甚至不及架构一般的时间，虽然都知道要递归，但在哪里递归，怎么递归，都是一个很重要的问题。最后我采取对于括号内部进行递归，每一对括号内部都是另一个表达式，建一个新的Formula类，在输入的同时将括号的那种进行替换，替换后的表达式并没有嵌套因子，也就可以采用正则表达式进行判断，而由于递归定义，括号内的表达式自身，也会进行合法性判断，同时读入时就建立好完整的表达式数，首先是Formula类包含整个表达式，使用一个Term数组进行存储，而Term内部，是一个抽象类Factor数组，Factor类包括了Constant，Sin，Cos，Power，Expression五个子类，自此整个表达式就可以用一个Formula类储存下来，然后在每一个类中都包含Derivation方法，Formula和Term层面都是向下传递，到了Factor层面才真正开始求导，也就解决了求导问题，同时每个类也都有一个Output方法，依次输出。