KMP算法

    // TODO: 2018/4/9 比较重要的KMP算法 要理解 并且可以手写出来
    @Test
    public void testKMP(){
        char[] str = "bacbababadababacambabacaddababacasdsd".toCharArray();
        char[] ptr = "ababaca".toCharArray();
        int a = KMP(str, 36, ptr, 7);
        System.out.println(a);
    }

计算next数组：

   public void cal_next(char[] str, int[] next, int len)
    {
        next[0] = -1;//next[0]初始化为-1，-1表示不存在相同的最大前缀和最大后缀
        int k = -1;//k初始化为-1
        for (int q = 1; q <= len-1; q++)
        {
            while (k > -1 && str[k + 1] != str[q])//如果下一个不同，那么k就变成next[k]，注意next[k]是小于k的，无论k取任何值。k标识的是已经有几个位置是一样的了
            {
                k = next[k];//往前回溯
            }
            if (str[k + 1] == str[q])//如果相同，k++
            {
                k = k + 1;
            }
            next[q] = k;//这个是把算的k的值（就是相同的最大前缀和最大后缀长）赋给next[q]
        }
    }

KMP算法：

 // KMP算法
    int KMP(char[] str, int slen, char[] ptr, int plen)
    {
    int[] next = new int[plen];
        cal_next(ptr, next, plen);//计算next数组
        int k = -1;
        for (int i = 0; i < slen; i++)
        {
            while (k >-1&& ptr[k + 1] != str[i])//ptr和str不匹配，且k>-1（表示ptr和str有部分匹配）
                k = next[k];//往前回溯
            if (ptr[k + 1] == str[i])
                k = k + 1;
            if (k == plen-1)//说明k移动到ptr的最末端
            {
                //cout << "在位置" << i-plen+1<< endl;
                //k = -1;//重新初始化，寻找下一个
                //i = i - plen + 1;//i定位到该位置，外层for循环i++可以继续找下一个（这里默认存在两个匹配字符串可以部分重叠），感谢评论中同学指出错误。
                return i-plen+1;//返回相应的位置
            }
        }
        return -1;
    }

String str = "bacbababadababacambabacaddababacasdsd";// 长度为n


String ptr = "ababaca";// 长度为m


最笨的办法是拿着长度为m的ptr子串到长度为n的str串中逐一去匹配，每次匹配的时候str的步数是1，ptr的步数也是1.所以时间复杂度就是O((n-m)*m);

KMP算法是充分利用了目标字符串ptr的性质，比如里面部分字符串的重复性，即使不存在重复字段，在比较时，实现最大的移动量，

每次匹配的时候str的步数是1，ptr的步数用可能的最大的移动量，也就是next数组的值。

 

第一步：计算next数组

概念：相同的最长前缀和最长后缀的长度

这里的前缀，后缀的概念：

String ptr = "ababaca"的最长前缀是“ababac”，

前缀：不能包括最后一个字符，

后缀概念也相同，不能包括第一个字符 。

 

对于目标字符串："ababaca" 有如下

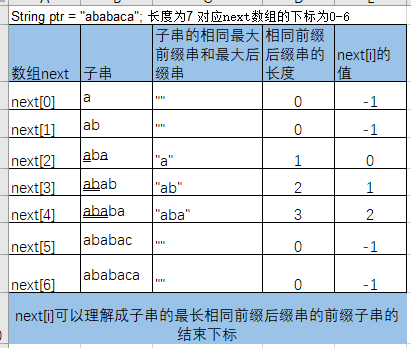
 next数组就是最大的移动量，在计算next数组的时候，

int k，就是累计已经匹配相同的前缀后缀子串前缀的下标，到下一个元素的时候，看这个元素是否相等，

若相等，k再次累加1，如果不相等，k=next[k],犹豫k是目前已经累积相等的子串的长度的下标，所以next[k]一定小于k

 第二步：利用next数组的计算结果来匹配

在这一步里 k标记的是ptr串中累计的已经匹配的长度的下标值。待k累计到ptr的长度-1 m-1的时候，就表示完整匹配到了目标子串。