相似度计算方法总结

1. 皮尔森相关系数

1.1 相关系数

考察两个事物（在数据里我们称之为变量）之间的相关程度。如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：

• 当相关系数为 0 时，X 和 Y 两变量无关系
• 当 X 的值增大（减小），Y 值增大（减小），两个变量为正相关，相关系数在 0.00 与 1.00 之间
• 当X的值增大（减小），Y值减小（增大），两个变量为负相关，相关系数在 -1.00 与 0.00 之间

相关系数的绝对值越大，相关性越强，相关系数越接近于 1 或 -1 ，相关度越强，相关系数越接近于 0，相关度越弱。

通常情况下通过以下取值范围判断变量的相关强度：

相关系数	相关度
0.8-1.0	极强相关
0.6-0.8	强相关
0.4-0.6	中等程度相关
0.2-0.4	弱相关
0.0-0.2	极弱相关或无相关

1.2 皮尔森(Pearson)相关系数

两个连续变量 (X,Y) 的 pearson 相关性系数(Px,y)等于它们之间的协方差cov(X,Y) 除以它们各自标准差的乘积 (σX,σY)。系数的取值总是在 -1.0 到 1.0 之间，接近 0 的变量被称为无相关性，接近 1 或者 -1 被称为具有强相关性。

• 皮尔逊系数是对称的：Corr(X, Y) = Corr(Y, X)。
• 皮尔逊相关系数有一个重要的数学特性是，因两个变量的位置和尺度的变化并不会引起该系数的改变，即它该变化的不变量(由符号确定)。也就是说，如果把 X 移动到 a+bX 和把 Y 移动到 c+dY (其中a、b、c和d是常数)，并不会改变两个变量的相关系数（该结论在总体和样本皮尔逊相关系数中都成立）。

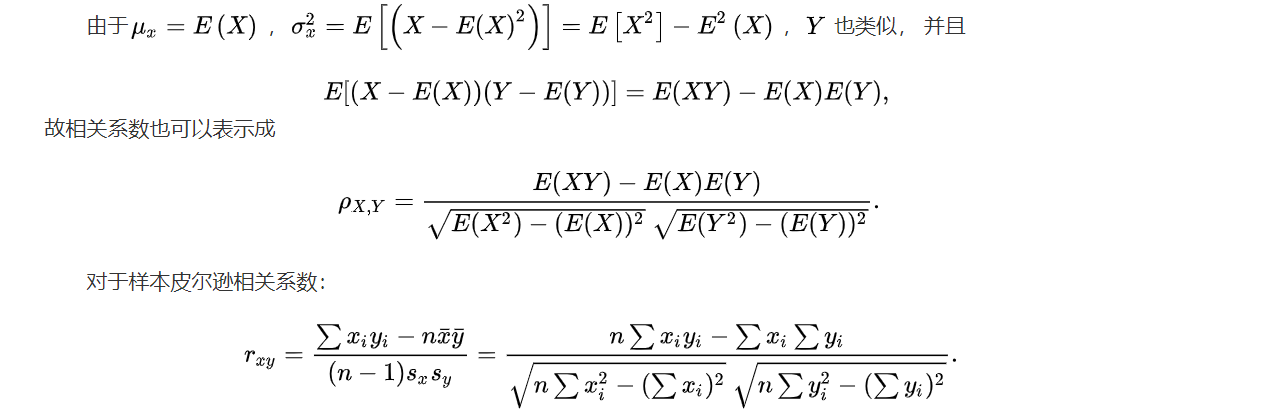
def pearson(vector1, vector2):
    n = len(vector1)

    #simple sums
    sum1 = sum(float(vector1[i]) for i in range(n))
    sum2 = sum(float(vector2[i]) for i in range(n))

    #sum up the squares
    sum1_pow = sum([pow(v, 2.0) for v in vector1])
    sum2_pow = sum([pow(v, 2.0) for v in vector2])

    #sum up the products
    p_sum = sum([vector1[i]*vector2[i] for i in range(n)])

    #分子num，分母den
    num = p_sum - (sum1*sum2/n)
    den = math.sqrt((sum1_pow-pow(sum1, 2)/n)*(sum2_pow-pow(sum2, 2)/n))
    if den == 0:
        return 0.0

    return num/den

用两个向量测试：
vector1 = [2,7,18,88,157，90,177,570]
vector2 = [3,5,15,90,180, 88,160,580]
运行结果为 0.998，可见这两组数是高度正相关的。

2. 欧几里德距离相似度

使用欧几里德距离来计算相似度是所有相似度计算里面最简单、最易理解的方法。它以经过人们一致评价的物品为坐标轴，然后将参与评价的人绘制到坐标系上，并计算他们彼此之间的直线距离。

\[d(x, y) = \sqrt{\sum{(x_i - y_i)^2}} \]

计算出来的欧几里德距离是一个大于0的数，为了使其更能体现用户之间的相似度，可以把它规约到 (0, 1] 之间：

\[sim(x, y) = \frac{1}{1 + d(x, y)} \]

• 只要至少有一个共同评分项，就能用欧几里德距离计算相似度
• 如果没有共同评分项，那么欧几里德距离也就失去了作用

其实照常理理解，如果没有共同评分项，那么意味着这两个用户或物品根本不相似。

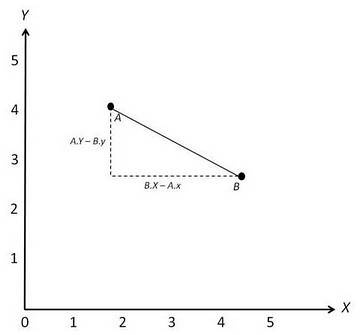
图中，用户A和用户B分别对项目X、Y进行了评分。用户A对项目X的评分为1.8，对项目Y的评分为4，表示到坐标系中为坐标点A(1.8, 4)；同理，用户B对项目X、Y的评分表示为坐标点B(4.5, 2.5)，因此他们之间的欧几里德距离（直线距离）为：sqrt((B.x - A.x)^2 + (A.y - B.y)^2)。

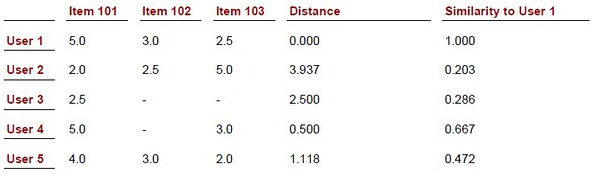
规约：

3. 余弦相似度

一个向量空间中两个向量夹角间的余弦值作为衡量两个个体之间差异的大小，余弦值接近 1，夹角趋于 0°，表明两个向量越相似，余弦值接近于 0，夹角趋于 90°，表明两个向量越不相似。

余弦函数在三角形中的计算公式为：

\[cos(θ) = \frac{a^2+b^2-c^2}{2ab} \]

在直角坐标系中，向量表示的三角形的余弦函数：

• 设向量 a 用坐标\((x_1, y_1)\)表示，向量 b 用坐标\((x_2, y_2)\)表示，则在直角坐标中的长度分别为\(|a| = \sqrt{(x_1)^2+(y_1)^2}\)，\(|b| = \sqrt{(x_2)^2+(y_2)^2}\)。
• 向量 c 表示向量 a 和向量 b 之间的距离，其在直角坐标系中的长度为\(|c| = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)。
• 代入三角函数的公式中得到：

\[\begin{align*} cos(θ) &= \frac{a^2+b^2-c^2}{2ab}\\ &= \frac{(x_1)^2+(y_1)^2+(x_2)^2+(y_2)^2-(x_2-x_1)^2-(y_2-y_1)^2}{2\sqrt{(x_1)^2+(y_1)^2}\sqrt{(x_2)^2+(y_2)^2}}\\ &= \frac{x_1x_2+y_1y_2}{\sqrt{(x_1)^2 * (y_1)^2}\sqrt{(x_2)^2+(y_2)^2}} \end{align*}\]

多维空间余弦函数的公式：

\[cos(θ) = \frac{\sum_{i=1}^{n}(x_i × y_i)}{\sqrt{\sum_{i=1}^{n}(x_i)^2} × \sum_{i=1}^{n}(y_i)^2} = \frac{a · b}{||a|| × ||b||} \]

余弦相似度越小，距离越大。余弦相似度越大，距离越小。

3.1 案例1、物品相似度计算

假设有3个物品，item1，item2和item3，用向量表示分别为：

item1[1,1,0,0,1]，

item2[0,0,1,2,1]，

item3[0,0,1,2,0]，

即五维空间中的3个点。用欧式距离公式计算item1、itme2之间的距离，以及item2和item3之间的距离，分别是：

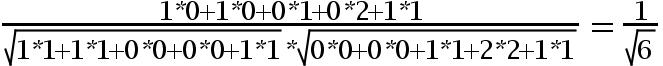
用余弦函数计算item1和item2夹角间的余弦值为：

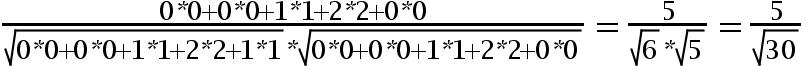
由此可得出item1和item2相似度小，两个之间的距离大(距离为7)，item2和itme3相似度大，两者之间的距离小(距离为1)。

余弦相似度算法：一个向量空间中两个向量夹角间的余弦值作为衡量两个个体之间差异的大小，余弦值接近1，夹角趋于0，表明两个向量越相似，余弦值接近于0，夹角趋于90度，表明两个向量越不相似。

3.2 案例2、文本的相似度计算

思路：
1、分词；
2、列出所有词(可以处理停用词)；
3、分词编码；
4、词频向量化；
5、套用余弦函数计量两个句子的相似度。

第一步，分词。

句子A：这只/皮靴/号码/大了。那只/号码/合适。

句子B：这只/皮靴/号码/不/小，那只/更/合适。

第二步，列出所有的词。

这只，皮靴，号码，大了。那只，合适，不，小，很

第三步，计算词频。

句子A：这只1，皮靴1，号码2，大了1。那只1，合适1，不0，小0，更0

句子B：这只1，皮靴1，号码1，大了0。那只1，合适1，不1，小1，更1

第四步，写出词频向量。

　　句子A：(1，1，2，1，1，1，0，0，0)

　　句子B：(1，1，1，0，1，1，1，1，1)

到这里，问题就变成了如何计算这两个向量的相似程度。我们可以把它们想象成空间中的两条线段，都是从原点（[0, 0, ...]）出发，指向不同的方向。两条线段之间形成一个夹角，如果夹角为0度，意味着方向相同、线段重合,这是表示两个向量代表的文本完全相等；如果夹角为90度，意味着形成直角，方向完全不相似；如果夹角为180度，意味着方向正好相反。因此，我们可以通过夹角的大小，来判断向量的相似程度。夹角越小，就代表越相似。
计算两个句子向量

句子A：(1，1，2，1，1，1，0，0，0)

和句子B：(1，1，1，0，1，1，1，1，1)的向量余弦值来确定两个句子的相似度。

计算过程如下：

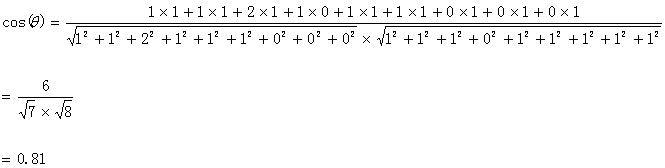
计算结果中夹角的余弦值为0.81非常接近于1，所以，上面的句子A和句子B是基本相似的。

由此，就得到了文本相似度计算的处理流程:

• 找出两篇文章的关键词；
• 每篇文章各取出若干个关键词，合并成一个集合，计算每篇文章对于这个集合中的词的词频
• 生成两篇文章各自的词频向量；
• 计算两个向量的余弦相似度，值越大就表示越相似。

3.3 案例3、购物网站文本的相似度计算

某购物网站有如下数据：小明购买了T恤a、T恤b、T恤e，小红购买了T恤b、T恤c、小强购买了T恤a、T恤e。
把以上信息转为向量图，代入上述的公式来计算得出相似度，过程如下：

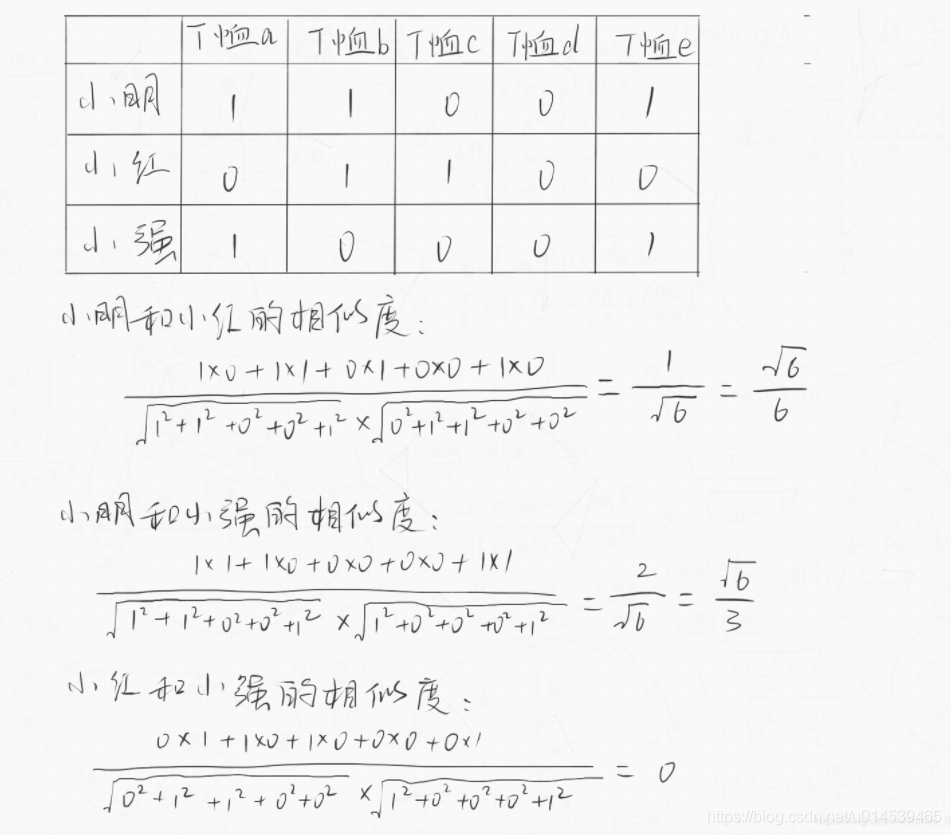
由上述的结果便可得到如下结论：小明和小红这两个用户有一定的相似度，但是不大，因为他们只有一个共同商品；小明和小强这两个用户相似度最大，因为他们有两个共同商品；而小红和小强的相似度为0，因为小红买的T恤小强都没有买。

原：https://blog.csdn.net/u014539465/article/details/105353638