【位运算】力扣461：汉明距离

两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y，计算并返回它们之间的汉明距离。
示例：

输入：x = 1, y = 4
输出：2
解释：
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。

注意： \(0 ≤ x, y < 2 ^ {31}\)
汉明距离广泛应用于多个领域。在编码理论中用于错误检测，在信息论中量化字符串之间的差异。
两个整数之间的汉明距离是对应位置上数字不同的位数。
根据以上定义，使用异或运算，记为 ⊕，当且仅当输入位不同时输出为 1。

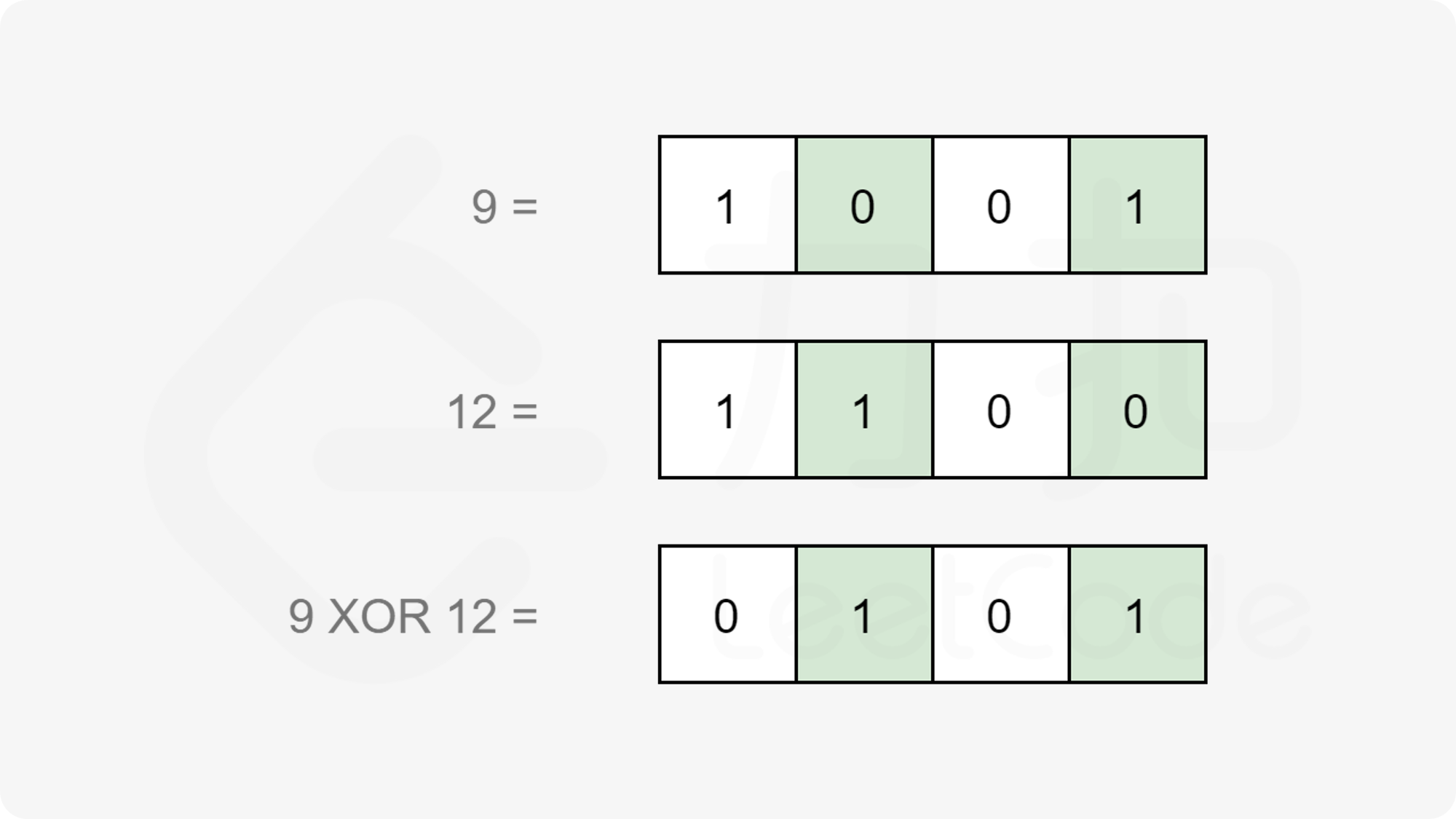
计算 x 和 y 之间的汉明距离，可以先计算 x ⊕ y，两个数字的异或结果，就是转化为二进制后按位比较的；然后统计结果中等于 1 的位数，那么原始问题转换为位计数问题。
当然，如果不知道这样的结果，也可以通过分别转化两个数成二进制数，然后前补零，按照两个字符串的方式按位比较，效率也很高。这里有个细节，具体前补多少零？因为 \(x, y < 2 ^ {31}\)，所以设置zfill(32)即可。
方法一：暴力字符串

class Solution:
    def hammingDistance(self, x: int, y: int) -> int:
        sx, sy = bin(x)[2:].zfill(32), bin(y)[2:].zfill(32) # 将整数x和y转换为二进制数，注意加上[2:]消除bin函数结果的前缀影响
        res = 0
        for i in range(32):
            if sx[i] != sy[i]:
                res += 1
        return res

方法二：内置位计数功能

class Solution:
    def hammingDistance(self, x: int, y: int) -> int:
        return bin(x ^ y).count('1') # 注意count的是字符串1，因为bin函数返回值是字符串

时间复杂度：O(1)。
空间复杂度：O(1)。

方法二：移位实现位计数
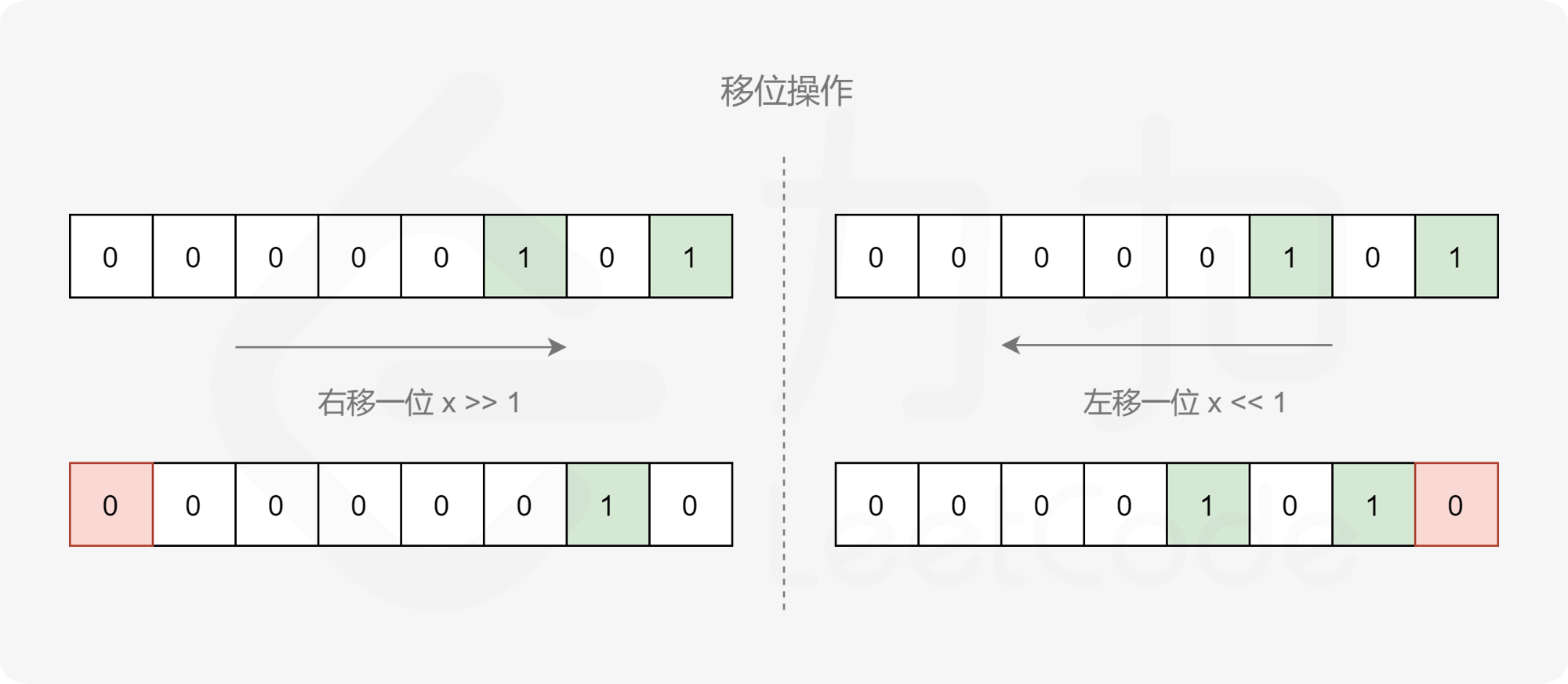
记 s=x⊕y，可以不断地检查 s 的最低位，如果最低位为 1，那么令计数器加一，然后我们令 s 整体右移一位，这样 s 的最低位将被舍去，原本的次低位就变成了新的最低位。重复这个过程直到 s=0 为止。这样计数器中就累计了 s 的二进制表示中 1 的数量。

class Solution:
    def hammingDistance(self, x: int, y: int) -> int:
        s = x ^ y # 计算异或
        res = 0
        while(s):
            res += s & 1 # ？？？
            s >>= 1 # 右移一位
        return res

时间复杂度：O(logC)，其中 C 是元素的数据范围，在本题中 logC=log2^31=31。
空间复杂度：O(1)。

方法四：Brian Kernighan 算法
在方法三中，对于 \(s=(10001100)_{2}\)的情况，需要循环右移 8 次才能得到答案。而实际上，如果可以跳过两个 1 之间的 0，直接对 1 进行计数，那么就只需要循环 3 次即可。
可以使用 Brian Kernighan 算法进行优化，具体地，该算法可以被描述为这样一个结论：记 f(x) 表示 x 和 x−1 进行与运算所得的结果（即 f(x)=x & (x−1)），那么 f(x) 恰为 x 删去其二进制表示中最右侧的 1 的结果。

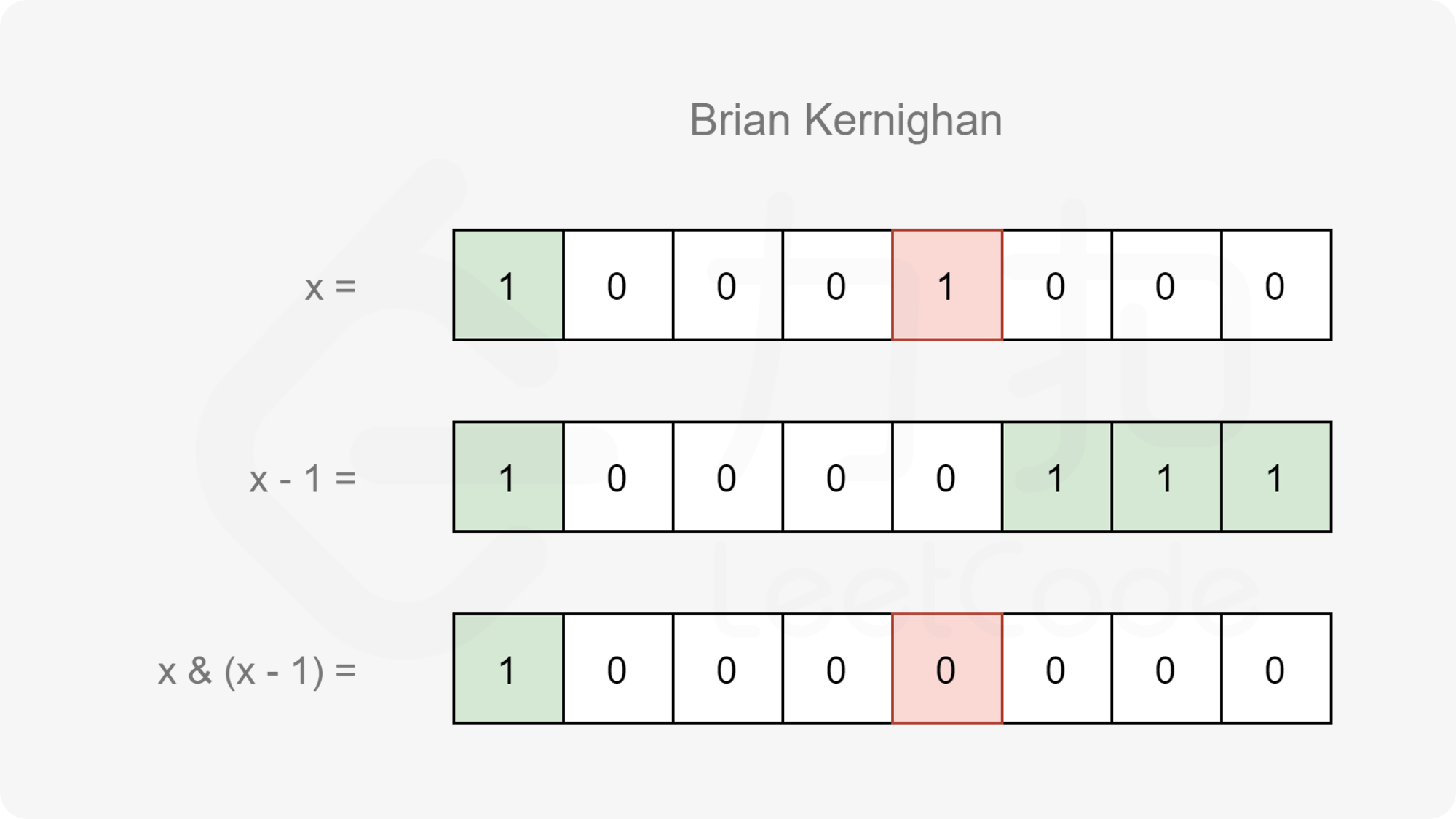
基于该算法，当计算出 s=x⊕y，只需要不断让 s=f(s)，直到 s=0 即可。这样每循环一次，s 都会删去其二进制表示中最右侧的 1，最终循环的次数即为 s 的二进制表示中 1 的数量。

class Solution:
    def hammingDistance(self, x: int, y: int) -> int:
        s = x ^ y
        res = 0
        while(s):
            s &= s - 1
            res += 1
        return res

时间复杂度：O(logC)，其中 C 是元素的数据范围，在本题中logC=log2^31=31。
空间复杂度：O(1)。