[LeetCode] 812. Largest Triangle Area_Easy tag: math

You have a list of points in the plane. Return the area of the largest triangle that can be formed by any 3 of the points.

Example:
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2
Explanation: 
The five points are show in the figure below. The red triangle is the largest.

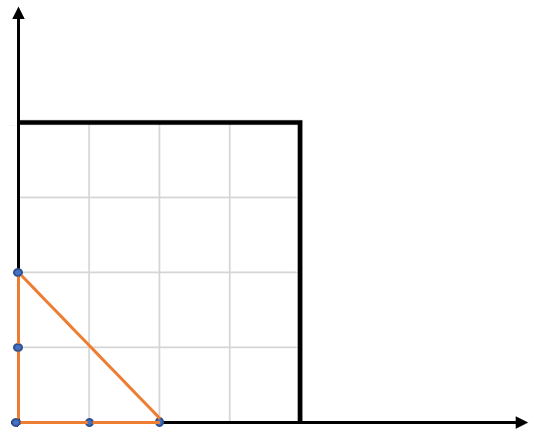
Notes:

• 3 <= points.length <= 50.
• No points will be duplicated.
•  -50 <= points[i][j] <= 50.
• Answers within 10^-6 of the true value will be accepted as correct.

 

Code:

利用itertools.combinations

同时利用

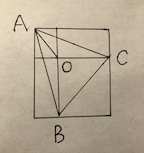
使OC为横轴， OB为纵轴， OBC成为直角三角形

S abc = S aob + S boc + S coa

          = 0. 5* OB * 高  + 0.5 * OB * OC  + 0.5 * OC * 高

          = 0.5 * (yc - yb) * (xb - xa)  + 0.5 * (yc - yb) * (xc - xb)  + 0.5 * (xc - xb) * (ya - yc)

          = 0.5 * (yc - yb) * (xb - xa)  +  0.5 * (xc - xb) * (yc - yb + ya - yc)

          = 0.5 * (yc - yb) * (xb - xa) + 0.5 * (xc - xb) *(ya - yb)

          = 0.5 (xa*yb + xb*yc + xc*ya - xa*yc - xc*yb - xb*ya)

NOTE：

0.5 * abs(((bx - ax)* (cy - by)) + ((by - ay)*(ax - cx)) + ((by - ay)*(bx - ax)))
不要将abs加入到里面，

0.5 * (abs((bx - ax)* (cy - by)) + abs((by - ay)*(ax - cx)) + abs ((by - ay)*(bx - ax))) Does not work!!!

 

          规律是三个相加，再三个相减，ab，bc，ca，ac，cb，ba 也是对称的

T: O(n ^3)

def largestTriangleArea(self, p):
        return max(0.5 * abs(xa*yb + xb*yc + xc*ya - xb*ya - xc*yb - xa*yc) for (xa, ya), (xb, yb), (xc, yc) in itertools.combinations(p, 3))

 

建combination function来得到combinations，再建一个getArea function去简化code

Code

class Solution(object):
    def largestTriangleArea(self, points):
        """
        :type points: List[List[int]]
        :rtype: float
        """
        ans = []
        self.helper(points, [], 0, ans)
        return max([  self.getArea(points_three) for points_three in ans])
    
    def getArea(self, points_three):
        (ax, ay) = points_three[0]
        (bx, by) = points_three[1]
        (cx, cy) = points_three[2]
        return 0.5 * abs(((bx - ax)* (cy - by)) + ((by - ay)*(ax - cx)) + ((by - ay)*(bx - ax)))
    
    def helper(self, points, temp, pos, ans):
        if len(temp) == 3:
            ans.append(temp)
        elif len(temp) < 3:
            for i in range(pos, len(points)):
                self.helper(points, temp + [points[i]], i + 1, ans)