堆排序

图片转载自：https://www.cnblogs.com/chengxiao/p/6129630.html

思想

1）堆排序是直接选择排序的改进，同属选择排序类

2）堆是具有以下性质的完全二叉树：每个节点的值都大于等于其左右孩子节点的值，称为大顶堆（最大堆）；或者每个节点的值都小于等于其左右孩子节点的值，称为小顶堆（最小堆）

2）将待排序序列构造成一个大顶堆，大顶堆的根节点就是最大值，将其与末尾元素进行交换，此时末尾成为最大值；然后将剩余n-1个元素重新构造成一个大顶堆，这样会得到次大值；不断重复上述操作，便能得到一个有序序列

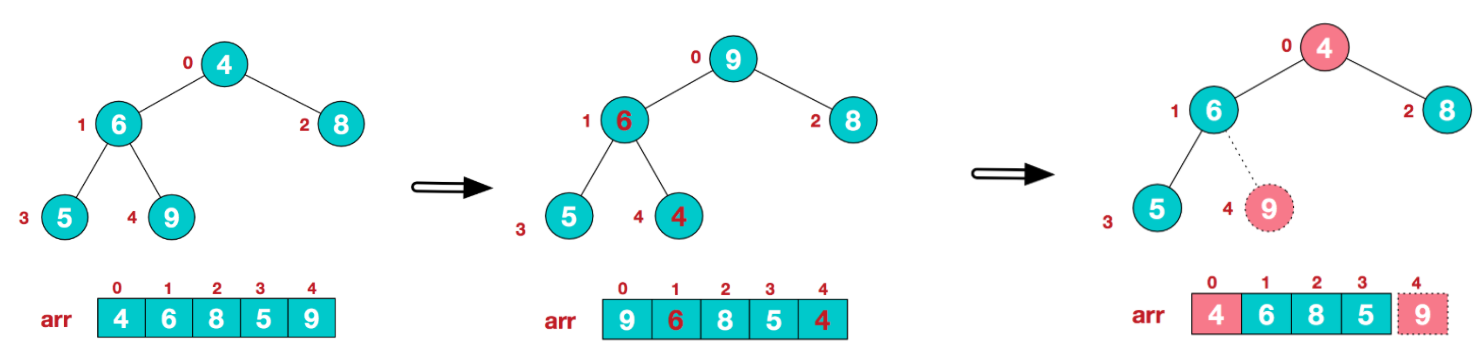
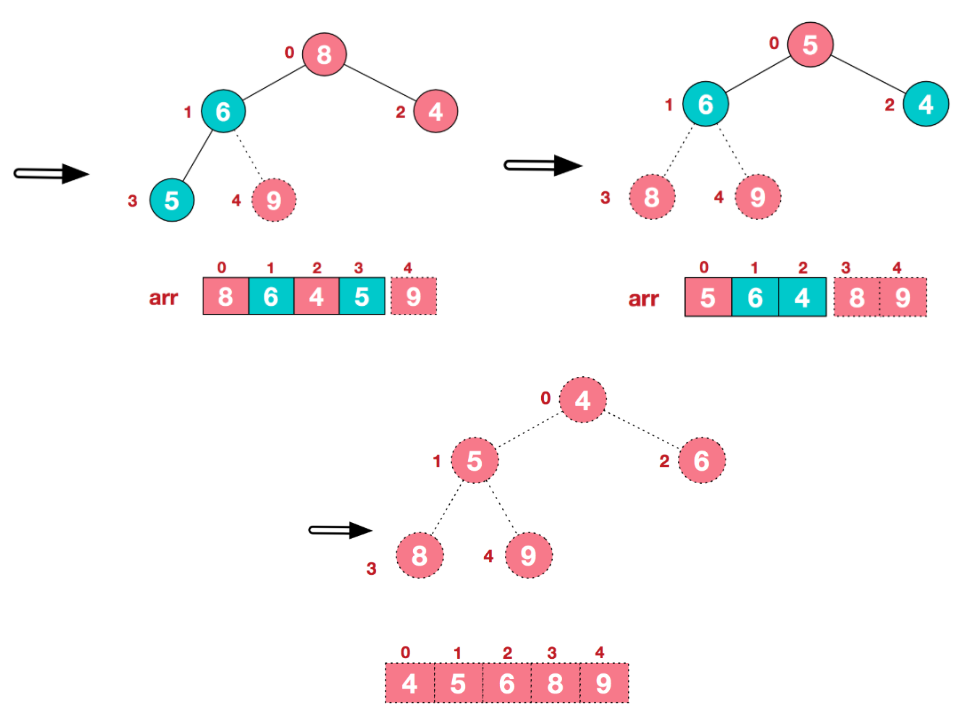
代码实现

void adjustHeap(vector<int>& nums, int node, int last)//调整完全二叉树，使得以node节点为根的树成为大顶堆
{
    int temp = nums[node];
    for (int i = 2 * node + 1; i <= last; i = 2 * i + 1)//沿较大的儿子向下进行调整
    {
        if (i <= last - 1 && nums[i] < nums[i + 1])//比较左儿子和右儿子的大小，让i指向更大的那个儿子
            ++i;
        //为temp寻找的一个正确的安放位置
        if (temp < nums[i])//此处仅仅是赋值，不是交换，这样可以减少交换次数；因为执行adjustHeap前是从最后一个分支节点开始往前遍历过一遍的，所以可以这么做
        {
            nums[node] = nums[i];
            node = i;//接着向下调整
        }
    }
    nums[node] = temp;
}

void makeHeap(vector<int>& nums)//构建大顶堆
{
    for (int i = nums.size() / 2 - 1; i >= 0; --i)//遍历所有的分支节点，从最后一个分支节点开始往前遍历，循环结束最后将得到大顶堆
        adjustHeap(nums, i, nums.size() - 1);
    /*
    for (int i = 0; i < nums.size(); ++i)
    cout << nums[i] << " ";
    cout << endl;
    */
}

void sortHeap(vector<int>& nums)//堆排序
{
    makeHeap(nums);//构建一个大顶堆
    for (int i = nums.size() - 1; i > 0; --i)
    {
        swap(nums[0], nums[i]);//将根节点换至数组末尾
        adjustHeap(nums, 0, i - 1);
    }
}



int main()
{
    //测试范例
    vector<int> vec{ 40,50,70,10,80,90,30,20,60,54,1 };
    sortHeap(vec);
    for (int i = 0; i < vec.size(); ++i)
        cout << vec[i] << " ";

    return 0;
}

时间复杂度

 　　最好情况、最坏情况、平均情况均是O(n logn)，由于初始构建堆所需的比较次数较多，所以不适合对元素个数较少的序列使用堆排序

空间复杂度

 　　O(1)

稳定性

　　堆排序可能会进行一些跳跃式的大顶堆调整，不能保证相同元素排序前后的相对位置不变，所以是不稳定的