可汗学院统计学 学习笔记
学习之前,需强调:概率是已知模型和参数,推数据;而统计是已知数据,推模型和参数。
第十二集:样本与总体
首先,为何需要样本呢?因为人类并不能总是获取总体数据,例如:人类的身高数据,全世界每秒都有人出生和死去,要获取总体数据是不现实的,故需要样本。样本就是从总体中抽取的一部分数据,人类希望用样本来估计总体,这样做可以节省人力物力而且可行,对么?其次,在统计学中,样本的均值通常用,总体的均值用
。均值,中位数,众数是用来衡量数据集中趋势。

第十三集:总体方差
总体方差是用来描述总体数据离散程度的统计工具。即数据偏离总体中间水平的程度,用符号来表示,请注意这是总体方差。下面会讲述样本方差。

第十四集:样本方差
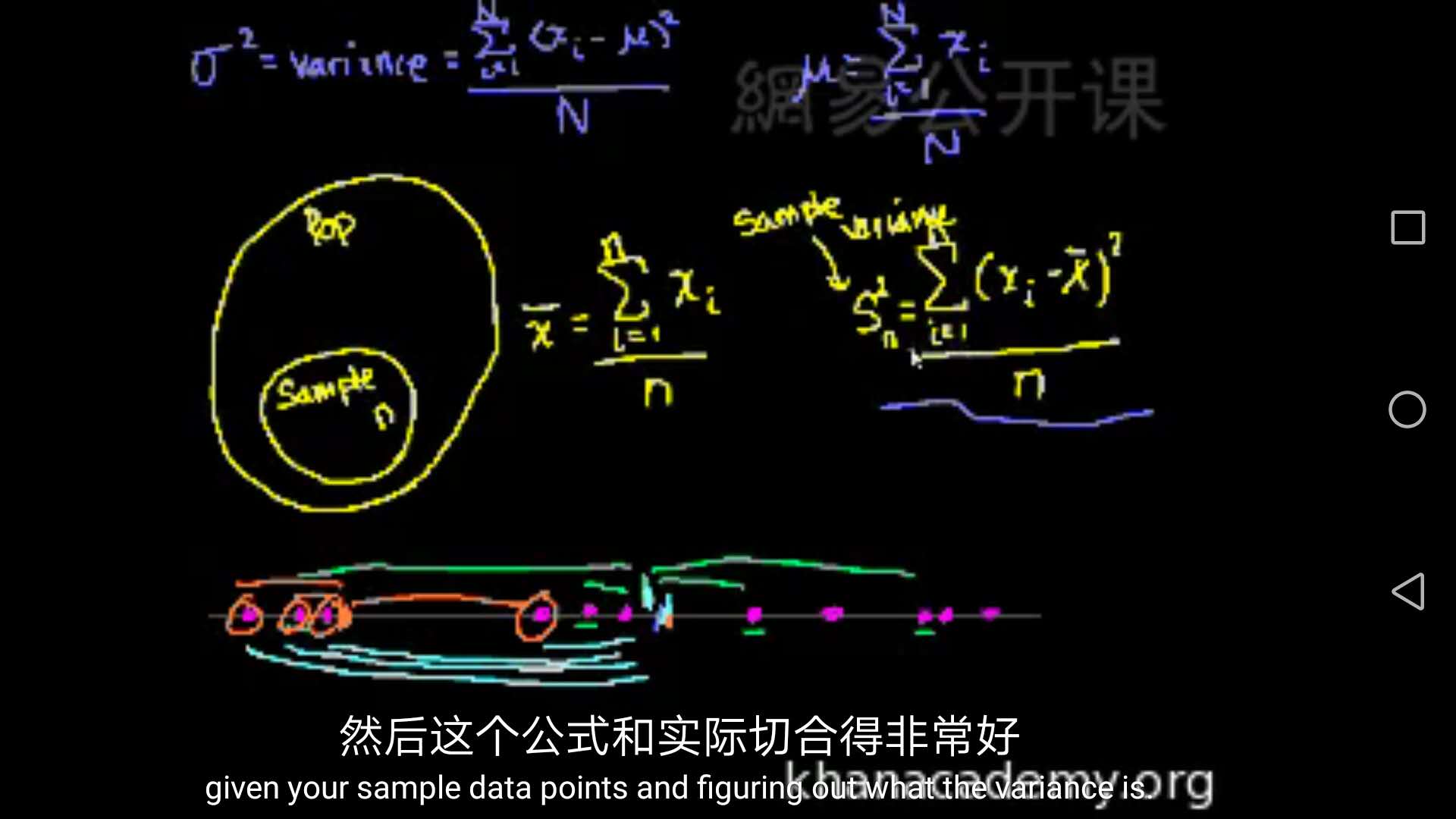
总体方差是用来描述样本数据离散程度的统计工具。即数据偏离样本中间水平的程度,用符号来表示,具体计算如图1,需注意均值为样本均值
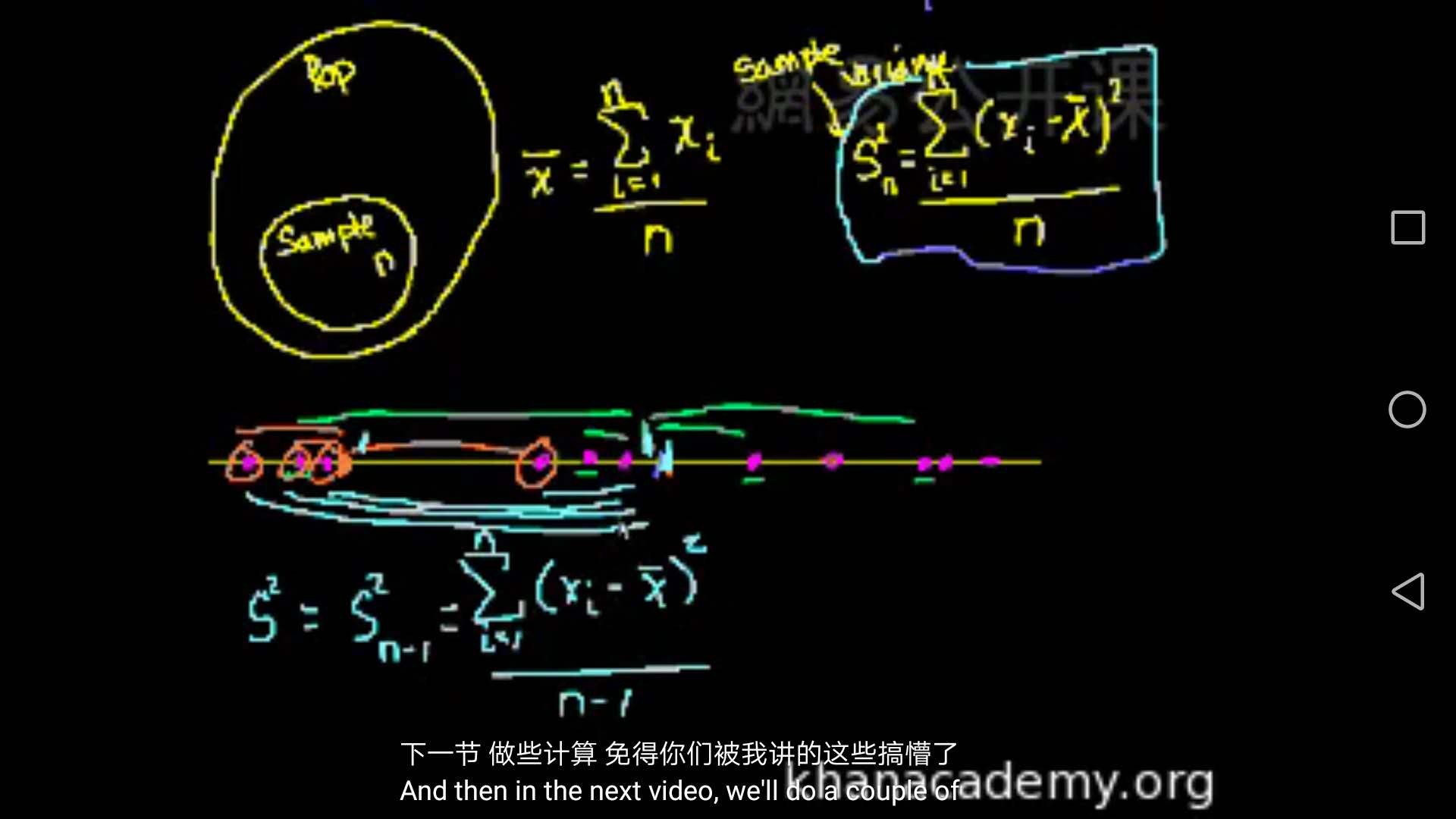
。图1算样本方差存在一个问题:就是样本集的选择问题,由于事前不知道样本的分布,选择样本集求均值时,容易出现偏差,如紫色的点,选取前四个会让样本均值偏大,从而导致样本方差低于总体方差。为避免这种情况,提供无偏估计,我们定义无偏样本方差
。如图2所示。
第十五集:标准差
标准差就是方差开平方,用表示。意义与方差一样,优点是直观。注意总体方差与样本方差的区别和联系。

第十六集:诸方差公式
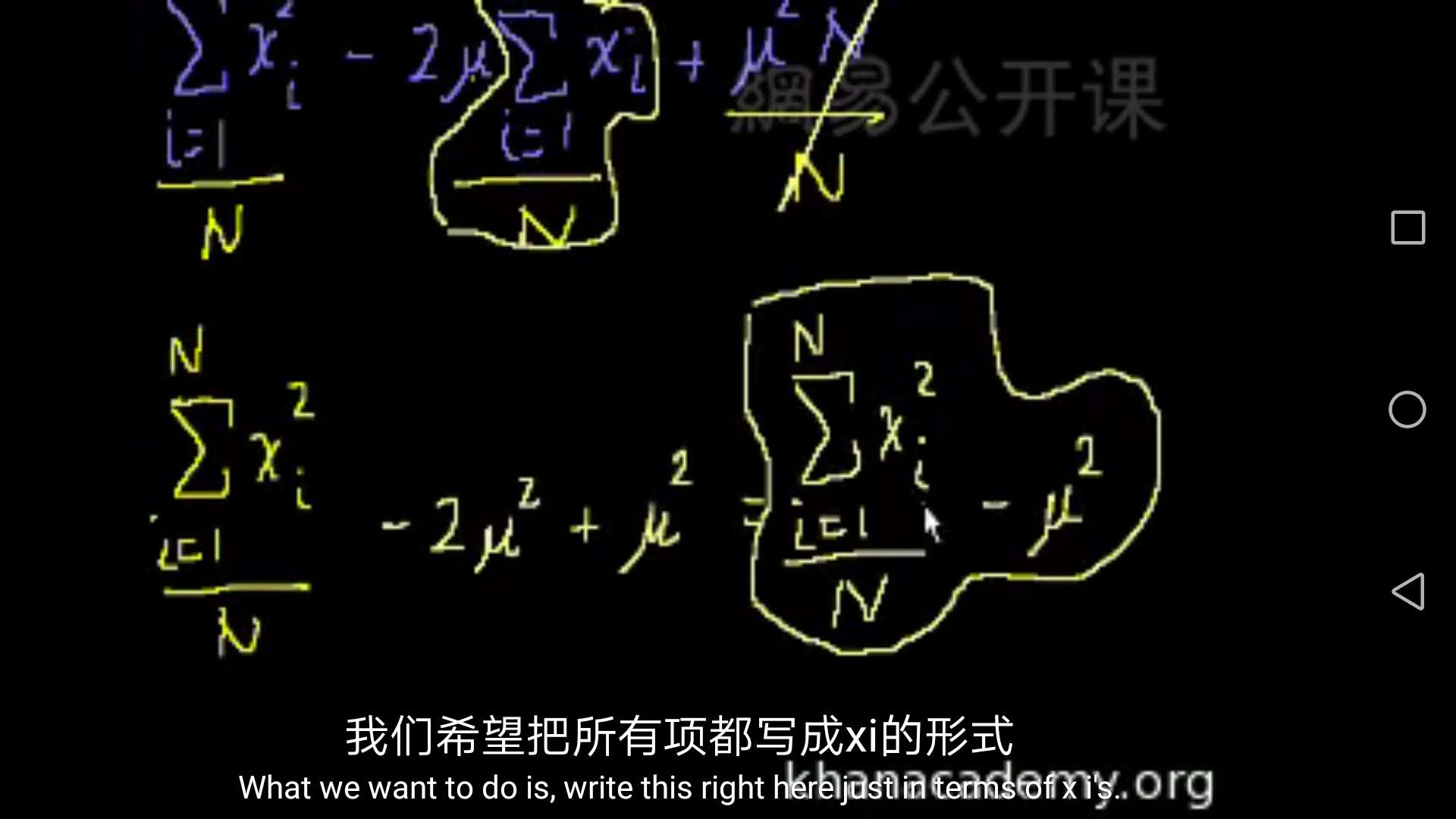
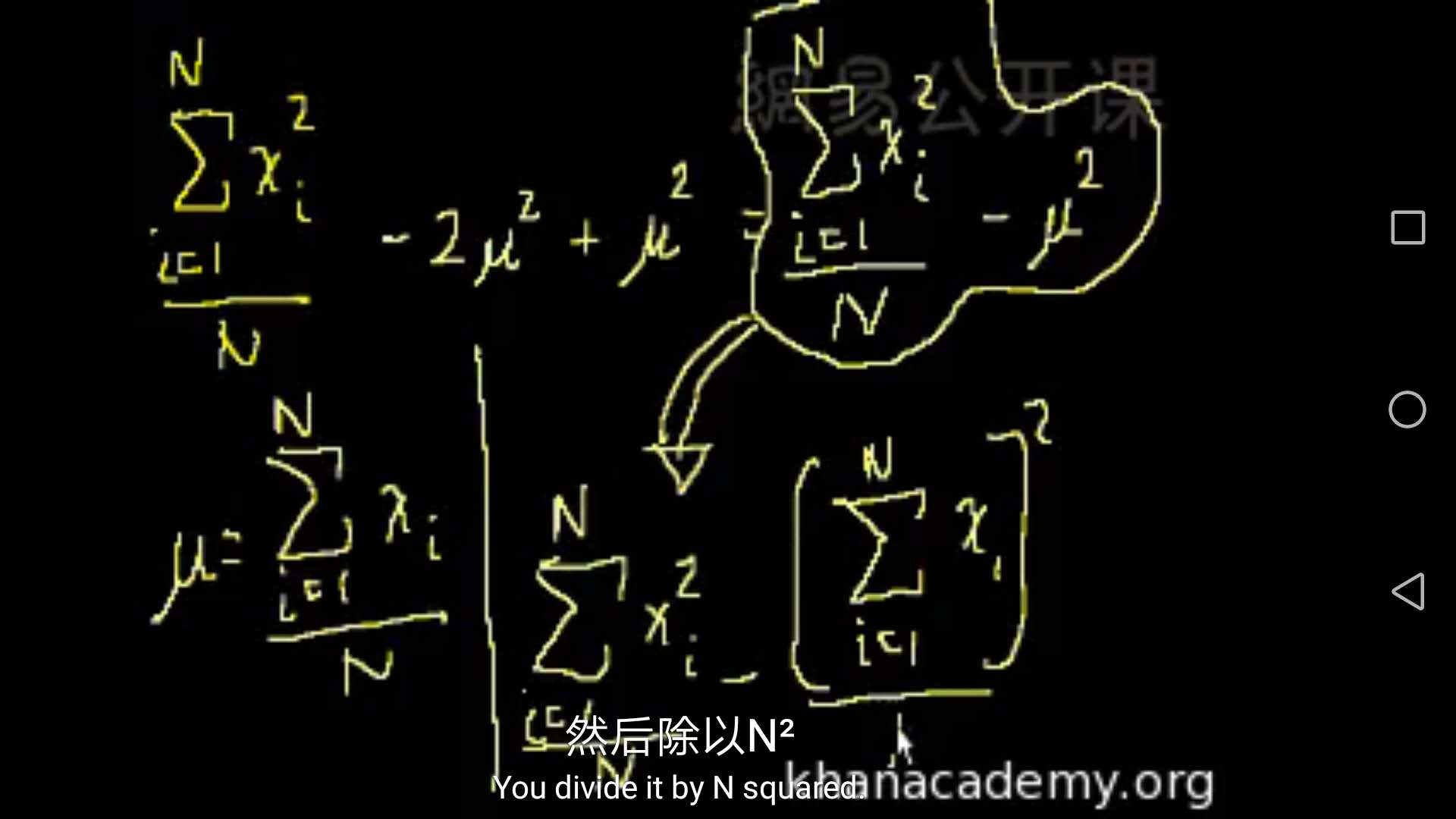
为了更快的计算方差,给出方差化简后的公式。黄线圈住的。
第十七集:随机变量介绍
随机变量与普通变量不同,因为随机变量通常是一个函数,用于量化随机过程。通常用大写字母X,Y,Z等表示,而传统变量通常用小写字母x,y,z表示。随机变量有两类:离散型和连续型。例如:明天是否下雨,用随机变量X来表示,它只有0,1两种值即取值有限且不连续,X是离散型随机变量;而对于明天下雨量,用Y表示,它可以取连续值0.1,0.2,0.5,0.511等,可以是无穷的数据,Y是连续型随机变量。

第十八集:概率密度函数
建议看这篇博客:https://www.jianshu.com/p/b570b1ba92bb。需要指出的是概率密度函数是针对连续性随机变量而言的。

第十八集-----二十二集 二项分布
这几节主要讲了二项分布的例子,便于理解。二项分布进阶的博客:https://blog.csdn.net/Michael_R_Chang/article/details/39188321。需注意的是二项分布针对的是离散型随机变量。
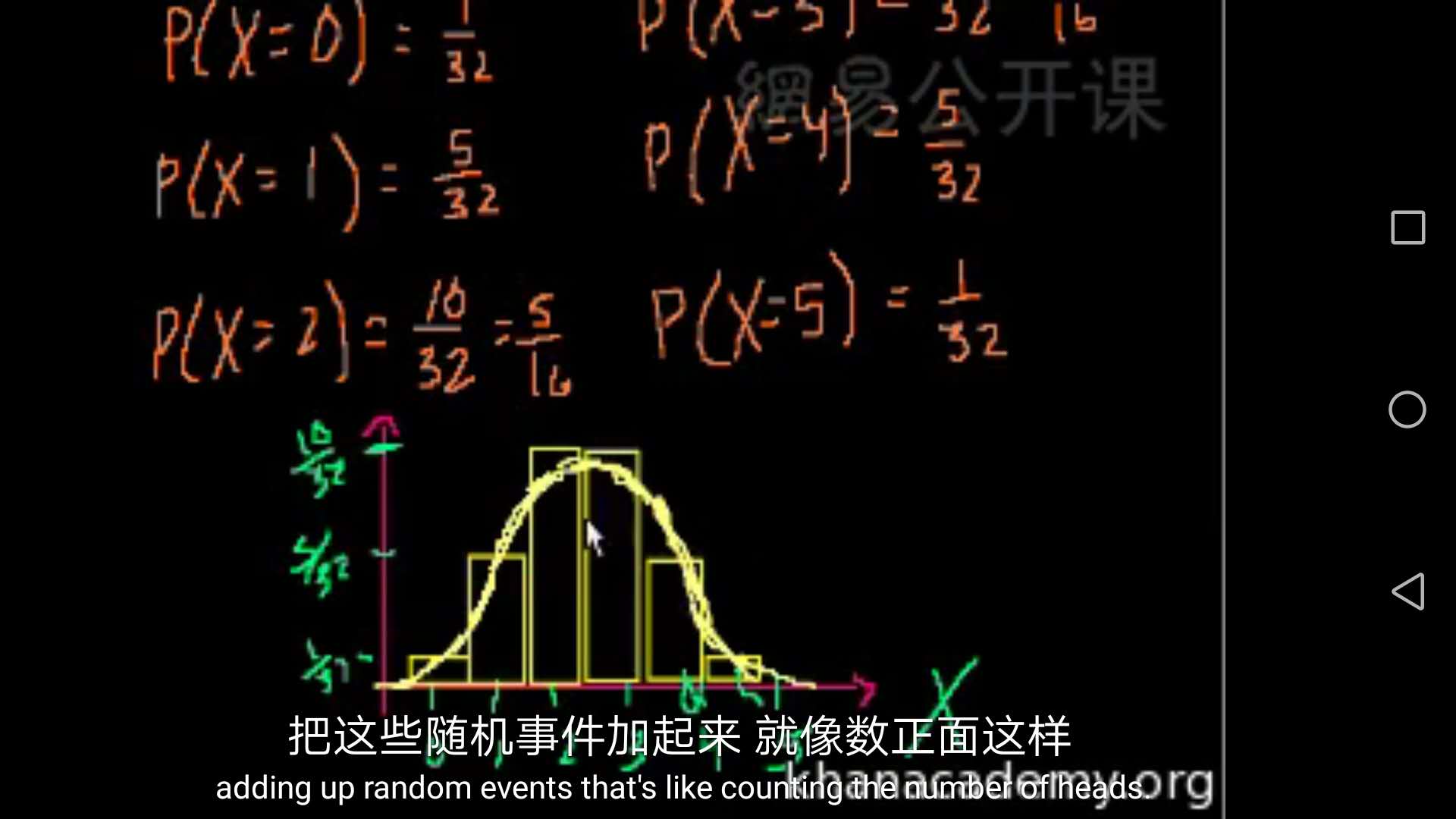
第二十三集:期望
随机变量的期望值其实是总体的均值,但有时由于总体样本无限多,用均值计算方法很难计算,故提出期望计算均值的方法.其思想是用频率作为权重计算出所有结果的加权平均值。

第二十四集:二项分布的期望值
对于二项分布的期望计算如图所示,本课有详细推导,感兴趣可以跟着推导一遍。
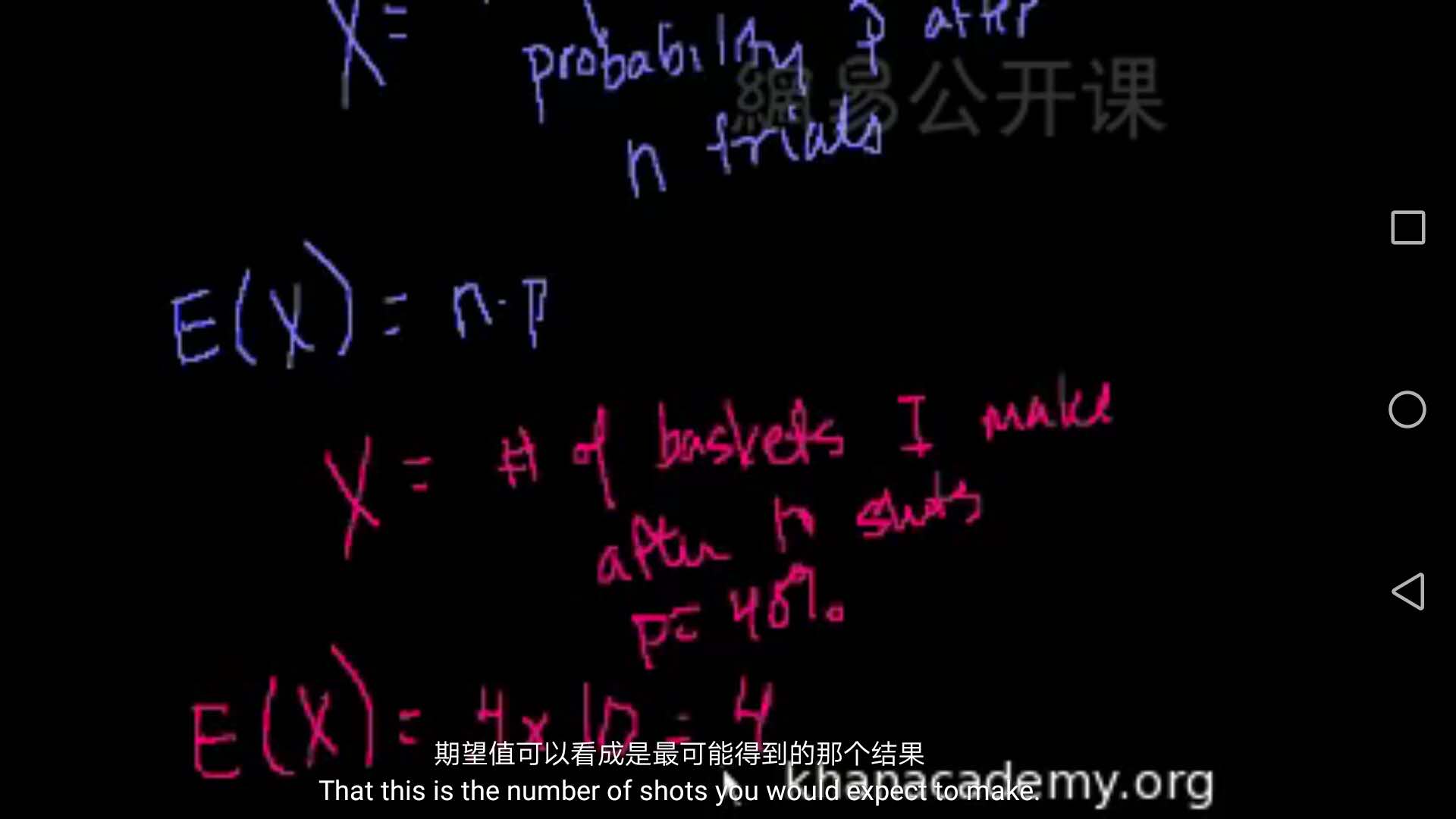
第二十五、六集:泊松过程
泊松分布是来自于二项分布。具体参见https://www.matongxue.com/madocs/858.html。在使用泊松分布前,我们应该知道它是用来求取某个时间段内发生事情x的概率有多大且其是离散分布。具体推导可以学习这章内容。


第二十七集 大数定律
大数定律描述了随机现象最根本的一个性质:平均结果的稳定性。大数定律告诉我们:对于独立同分布的随机序列,只要总体均值(随机变量期望)存在,则随着样本数的增加,样本均值会收敛到总体均值。注意样本数的足够性,概率是频率的一个极限值,这样可以避免赌徒谬误。http://blog.sciencenet.cn/blog-677221-1063741.html(赌徒谬误)
第二十八--三十四集 正态分布
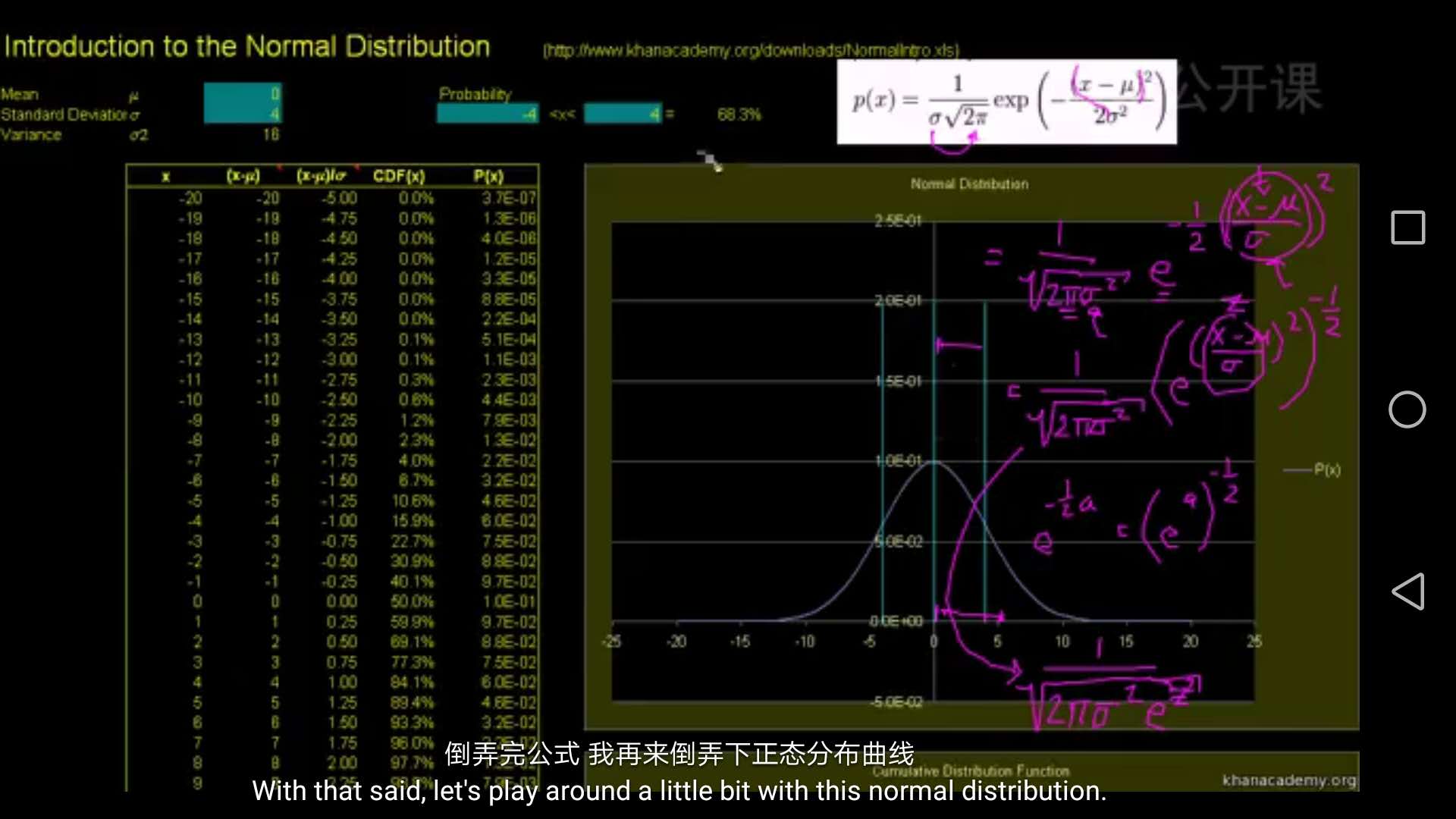
二项分布,泊松分布都是离散分布,而正态分布是连续分布。二项分布和泊松分布都可以转化为正态分布。泊松分布是,而正太分布是
为无穷大。图1是正态分布的概率密度函数图和表达式,图二是计算时使用的一些经验法则,具体说:与均值相差一个标准差概率是68%, 两个标准差概率是95%,三个标准差概率是99.7%。当然具体计算也可以查阅正态分布表。

第三十五集 中心极限定律
该定律是说随着样本n越来越大,这n个样本的m个均值会趋于正态分布。与大数定律的区别在于:大数定律描述的样本均值趋于总体均值,而中心极限定律描述的是样本均值的分布。
第三十六、七集 样本均值的抽样分布
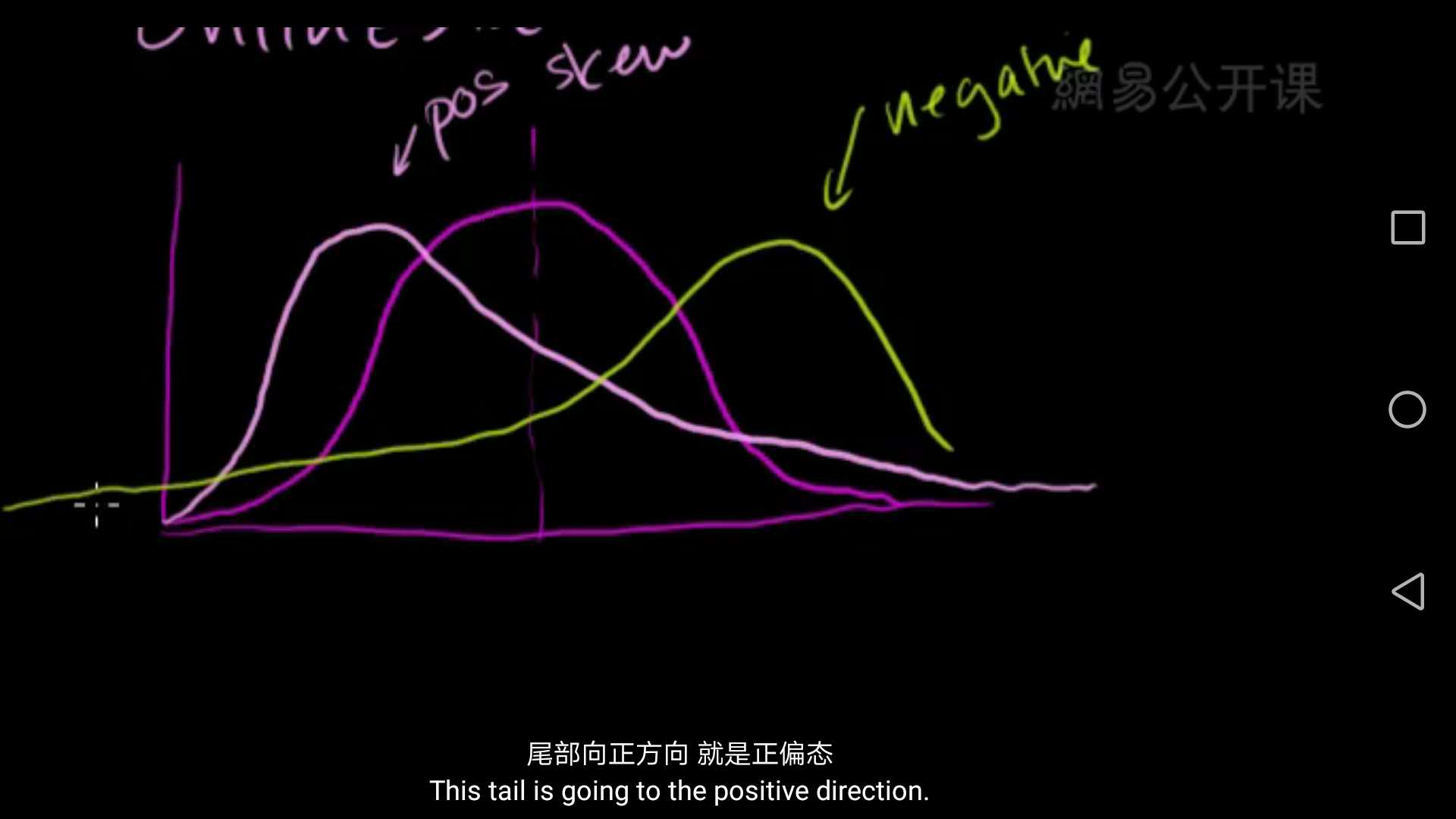
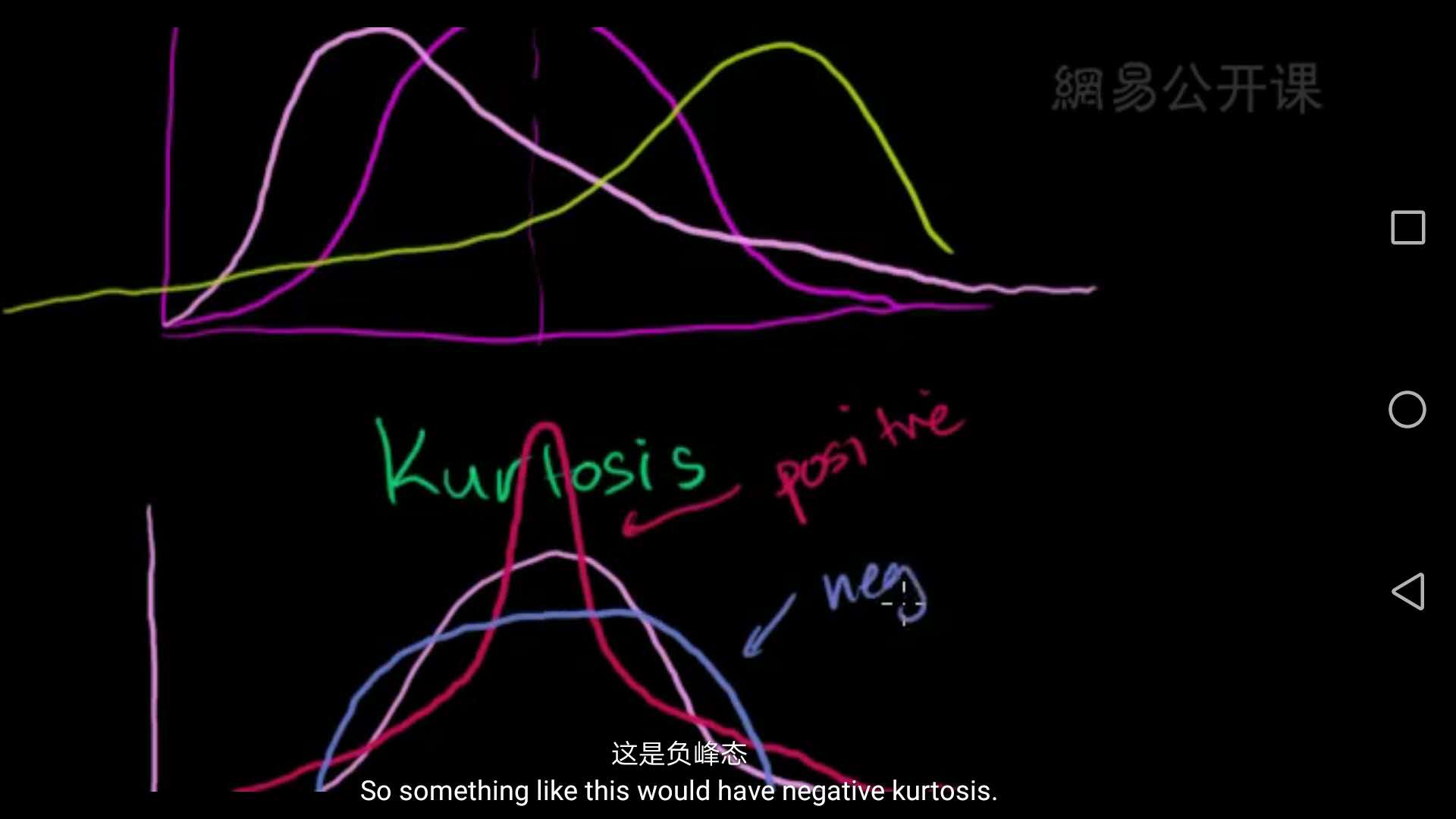
样本均值抽样分布是所有样本均值抽样形成的分布。其中偏度与峰度是描述一个分布有多像正态分布的物理量。其中正偏度表示数据正向的多,负偏度表示数据负向的多。峰度反映了锋部的尖度。
第三十八、九集 均值标准误差
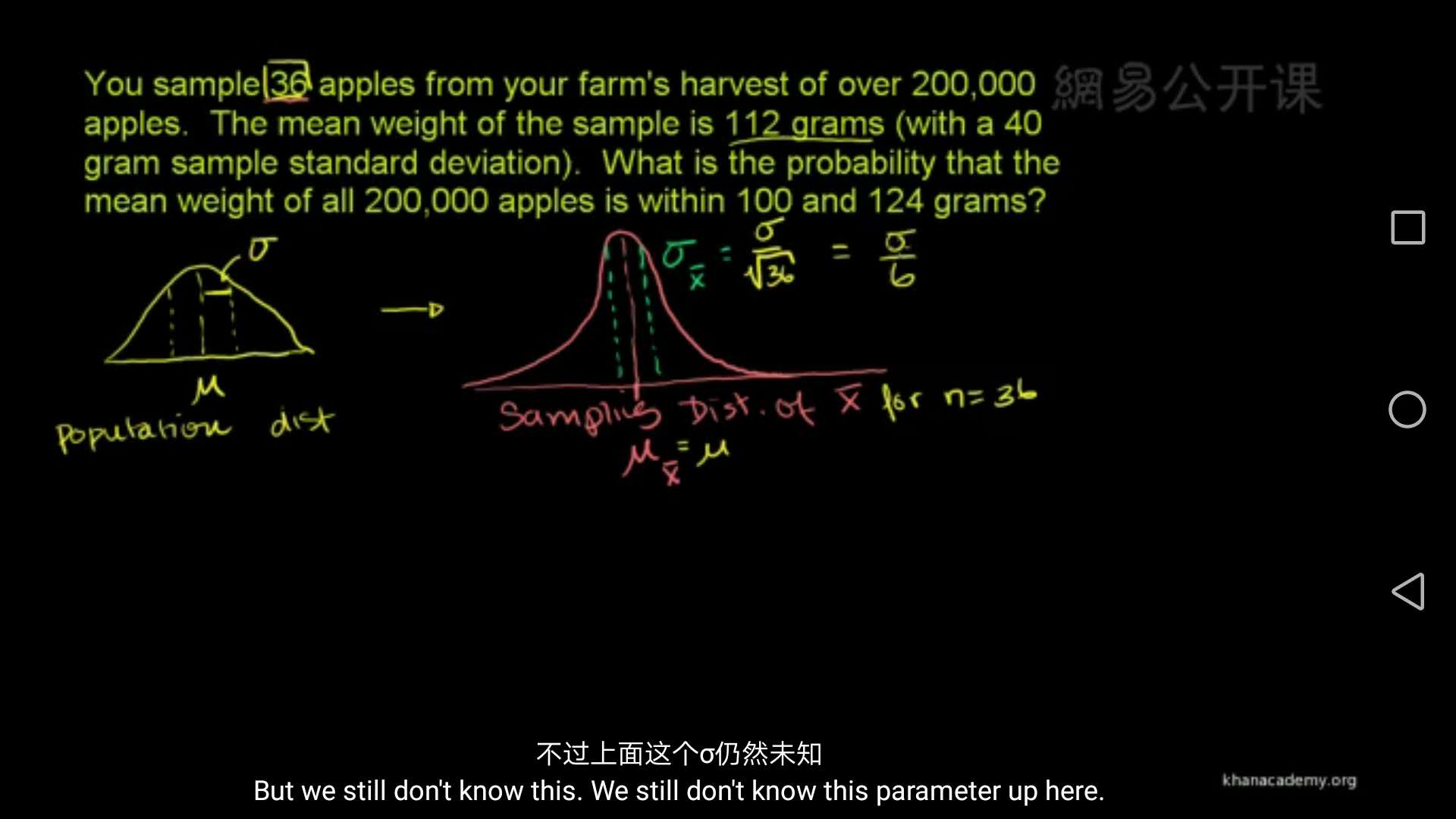
样本均值抽样分布是所有样本均值抽样形成的分布。均值标准差是样本均值抽样分布的标准差,其和总体标准差的关系为:

第四十、三、四集 置信区间与误差估计
在样本估计总体均值时,我们需要知道估计的准确度,因此选定一个区间[a,b],目的是让这个区间包含总体均值,这个区间叫做置信区间。对于这个区间有多大概率包含总体均值,这个概率称为置信水平。置信水平是根据实际问题自己确定的,一般设定为95%即两个标准差。总之:置信区间是我们计算变量的存在范围,置信水平是我们对这个范围的可信程度。
置信区间计算方法:首先,计算样本均值,样本均值标准差为
。这几个公式的问题是事先我们并不知道总体的标准差。因此我们需要用估计值来代替
。我们选择
样本方差作为总体方差的估计,需注意
是会跟随样本的变化而变化的,如图2所示。其次确定置信水平,最后查找z表格,计算置信区间。

第四十一、二集 伯努利分布
二项分布是n重伯努利实验成功次数的分布,个人认为放在二项分布之前讲解更好。伯努利分布又叫两点分布或者0-1分布。
第四十六集 小样本容量置信区间
当样本数量小于30时,样本分布不再符合正态分布而是符合T分布。T分布只有一个自由度参数n,当n趋于无穷时,T分布变为标准正态分布,其实T分布只是正态分布的一种近似,是正态分布在小样本时的形态。计算置信区间的方法和正态分布类似,不同的是要查t分布表而不是z分布表。
第四十七、八集 假设检验
假设检验与区间估计都是根据样本信息推断总体分布。两者可以相互装转换唯一的区别是参数知不知道的问题。举例来说:统计全校学生(总体)的平均上网时间(参数),如果参数未知,通过样本进行推断则是区间估计,如果有人已经得到平均上网时间(参数),而你不知道这个参数可不可靠,则是假设检验,换句话说无假设不检验。
P值主要是用来判断不同样本之间的差异是由抽样误差引起的还是总体不同引起的。在零假设条件下得到的概率称为P值。是判断标准也称为拒绝域,若P<
,则拒绝零假设,若相反,则接受零假设。计算P值方法为:1 确定样本均值与均值标准差,注意样本均值标准差为
,选择
样本方差作为总体方差的估计;2 求Z分数(T分数),查Z表(T表);3 确定概率值即P值。
需要注意一下:双侧检验是检验样本平均数和总体平均数有无明显差异,不管差异方向,如:视频中的药对小白鼠是正向作用还是反向作用不管,只管是否有作用;而单侧检验是考虑方向性的,即是正向作用还是反向作用。
第五十集 第一型错误
在假设检验中,接受或者拒绝H0,都有概率犯错误。第一类错误就是原假设为真,而检验的结论却劝你放弃原假设,称为弃真错误,出现的概率记为。如果原假设不是真,而检验的结论却劝你接受原假设称为取伪错误,出现的概率记为
。具体可参见: https://blog.csdn.net/m0_37777649/article/details/74937242
通常把只考虑犯第一类错误而不考虑第二类错误的假设检验称为显著性检验。一般约定俗成的有:0.05,0.025,0.01.显著水平与置信水平和为1.
第五十四集 随机变量之差的方差
这一章主要讲了一些推论,例如:独立变量的和差的期望等于各独立变量期望之和。
第五十四-六十一集 假设检验二
第六十二-七十集 决定系数R2
决定系数反映了Y的波动有多少百分比可以被X波动描述,这个系数是对回归方程拟合程度的判断。
其中表示第i个点的真实数据,
表示第i个点的预测数据。SSE也称为残差。
其中表示第i个点的真实数据,
表示均值。SST也称为总平方和,除以n-1,结果就是样本方差。
SSR称为残差平方和,表征预测值的偏离程度。
SST = SSR+SSE
其中称为决定系数,其值越大,自变量引起的变动占比越高,观察点在回归线附近越密集,拟合程度越好。
第六十九-七十集 例题
第七十一集 协方差
度量各个维度偏离其均值的程度。协方差是为多维变量创立的,目的是为了描述两个变量的关系(正相关,负向关。相互独立)。需注意协方差只能两个维度算,多个维度的协方差形成协方差矩阵。

第七十二集 卡方分布
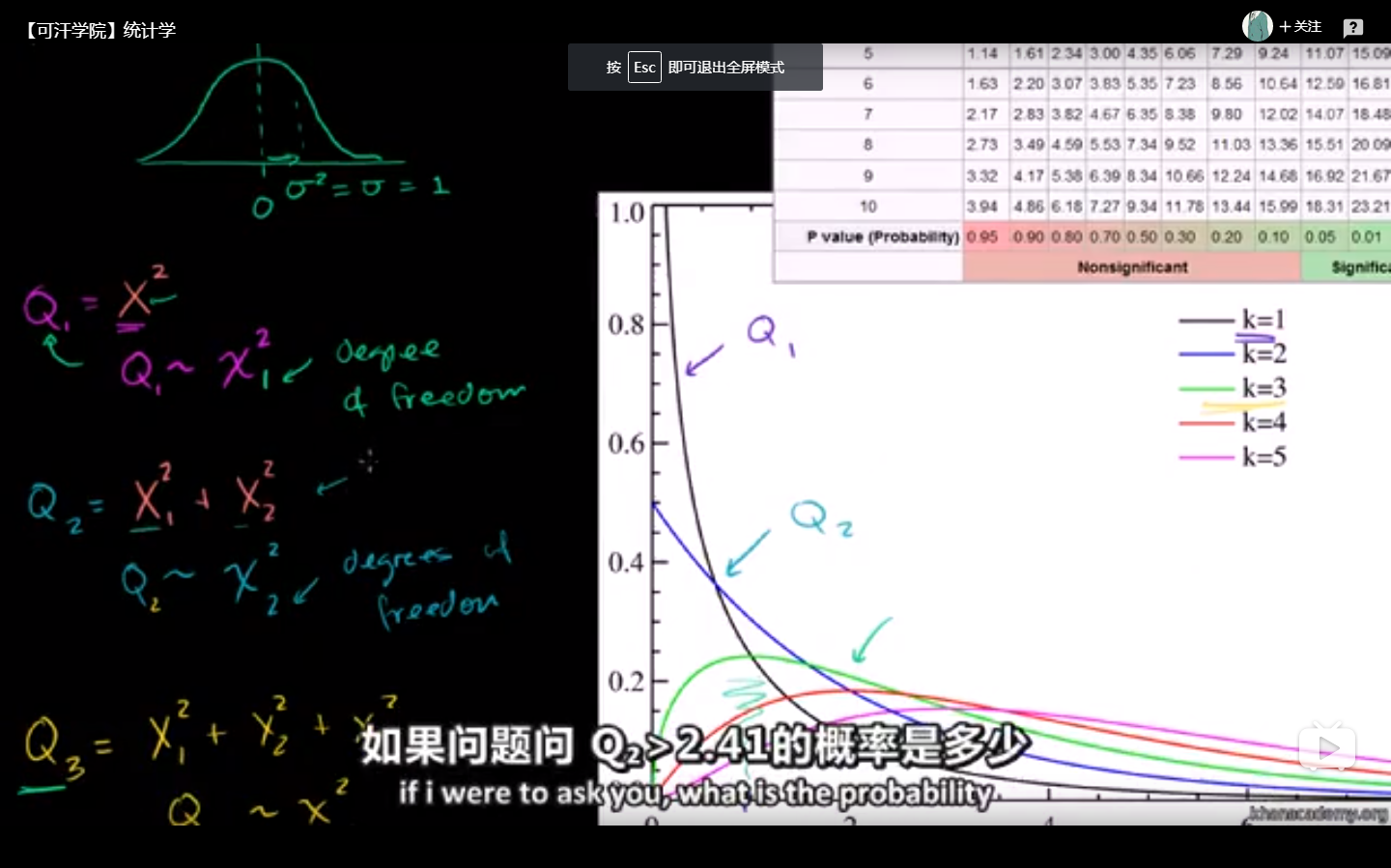
一些服从标准正态随机变量的平方求和即是分布,其中n为自由度,确定一个式子自由度的方法是:
若式子包含有n个独立的随机变量,和由它们所构成的k个样本统计量,则这个表达式的自由度为n-k.比如中包含ξ1,ξ2,…,ξn这n个独立的随机变量,
同时还有它们的平均数ξ这一统计量,因此自由度为n-1.。
第七十三、四集 卡方检验
卡方分布可以不用对总体做任何假设,卡方检验可以用来衡量观测与理论之间的拟合程度,或者推断两个分类变量是否相关或者独立。
具体例子可参考:https://blog.csdn.net/bitcarmanlee/article/details/52279907
第七十五、六集 平方和
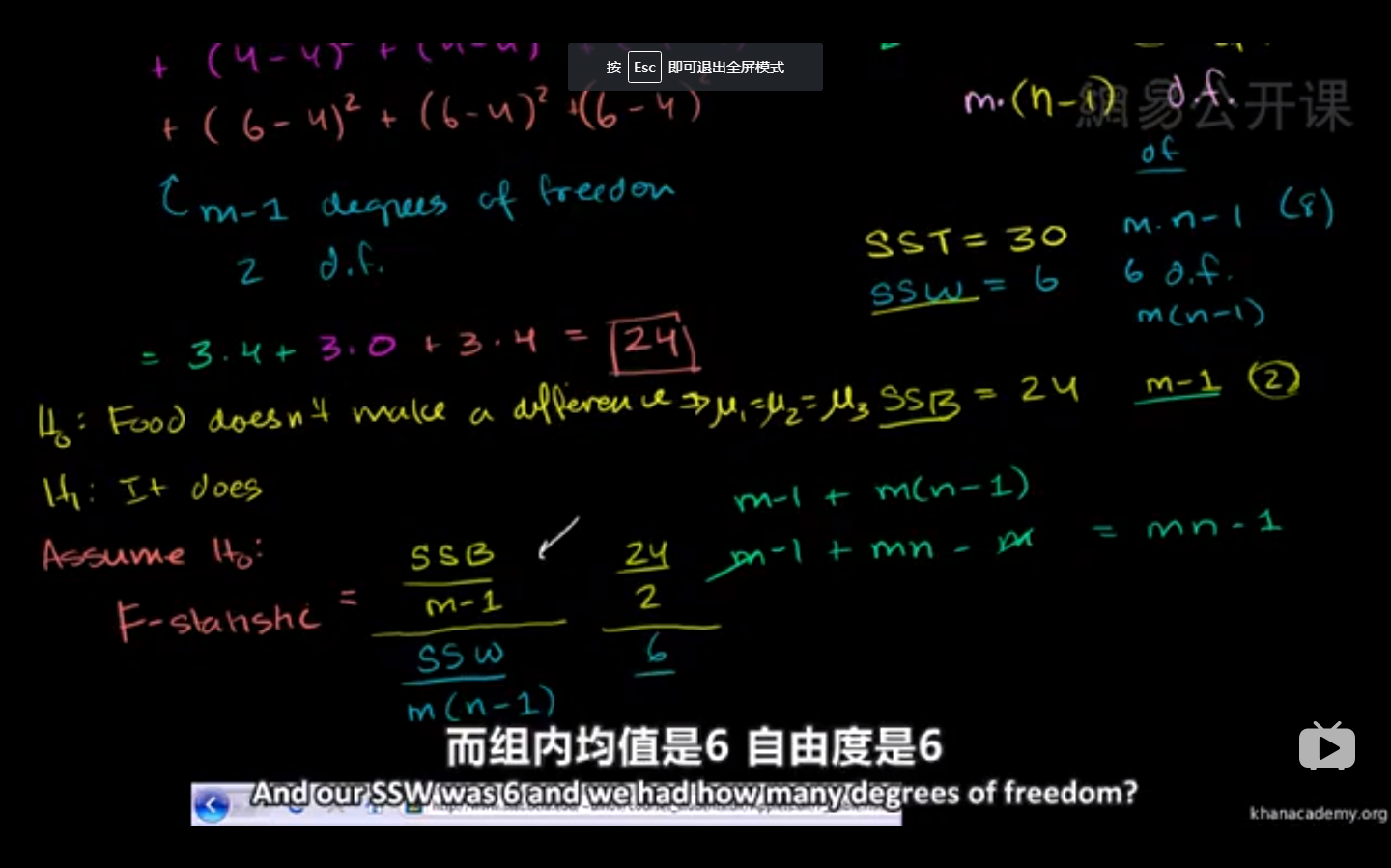
组内平方和:是每组的值减去每组自己的平均值,求平方和,组间平方和理解为两组之间的差异。
组间平方和:是每组自己的平均值减去总均值,求平方和,组内平方和理解为两组内部不同数据的差异。
如图:这几集的母的是为了说明总的波动=组内波动+组间波动
第七十七、六集 F假设检验
F统计量是组间平方和除以其自由度比上组内平方和除以其自由度。F值主要描述:组间的差异大,还是组内的差异大?如果是组间的差异大,那么这两组数据本身不一致的概率就大,对应F值比较大。F检验又称为方差其次性检验,检查的是方差的差异性。需注意:F检验的前提是F分布,而F分布的前提是正态分布。F检验通常作为T检验的一步。
各个分布的应用如下:
方差已知情况下求均值是Z检验。
方差未知求均值是t检验(样本标准差s代替总体标准差R,由样本平均数推断总体平均数)
均值方差都未知求方差是X^2检验
两个正态分布样本的均值方差都未知情况下求两个总体的方差比值是F检验。
第七十八集 相关性和因果性
相关性,描述两个随机变量是否存在线性关系。对于高斯过程,独立与不相关是等价的。此外,相关性和因果性是不同的,A与B相关,并不能说存在因果关系,也许是因为C与A相关,C与B相关,才导致A与B相关。
第七十九--八十五集 演绎推理与归纳推理
归纳推理是特殊到一般的过程,而演绎是一般到特殊的过程。




