几种常用排序算法代码实现和基本优化(持续更新ing..)
插入排序(InsertSort):
插入排序的基本思想:元素逐个遍历,在每次遍历的循环中,都要跟之前的元素做比较并“交换”元素,直到放在“合适的位置上”。
插入排序的特点:时间复杂度是随着待排数组的有序性变化的,数组越有序,插入排序的时间复杂度越低(接近O(n)级别),反之,时间复杂度越高(O(n*n)级别),平均情况是O(n*n)级别,所以我们日常使用时,只针对较为有序的数组进行插入排序,插入排序通常并不需要额外的数据存储空间,插入排序将数组分为无序区和有序区两个区,然后不断将无序区的第一个元素按大小顺序插入到有序区中去,最终将所有无序区元素都移动到有序区完成排序,所以插入排序通常是稳定的,但若将两层循环内部的判断条件加上等号,产生了“多余的”交换操作,此时插入排序又是不稳定的,不过没人会这样做;
#include <iostream> #include <algorithm> #include <string> #include <algorithm> #include "SortTestHelper.h" template<typename T> void insertSort(T arr[], int n ){ for(int i = 0; i < n-1; i++){ for(int j = i+1; j > 0; j--){ if(arr[j] < arr[j-1]){ swap(arr[j-1], arr[j]); }else{ break; } } } }
插入排序的优化:
由于在元素遍历的过程中,“交换”元素的时间代价总比“判断”的时间代价要大(“交换”元素需要三次赋值,而“判断”只要一次),故可以在第一层循环遍历元素的时候,将元素缓存,并循环判断,知道遇到“合适的位置”:
#include <iostream> #include <algorithm> #include <string> #include <algorithm> #include "SortTestHelper.h" template<typename T> void insertSort_Enhanced(T arr[], int n ){ for(int i = 0; i < n-1; i++){ T e = arr[i]; int j; for(j = i; j > 0 && arr[j-1] > e; j-- ){ arr[j] = arr[j-1]; } arr[j] = e; } }
归并排序(MergeSort):
归并排序的基本思想:基于分治策略(Divide and Conquer),将待排序序列R[0...n-1]看成是n个长度为1的有序序列,将相邻的有序表成对归并,得到n/2个长度为2的有序表;将这些有序序列再次归并,得到n/4个长度为4的有序序列;如此反复进行下去,最后得到一个长度为n的有序序列。
归并排序的特点:时间复杂度恒为O(nlogn)级别,归并排序是稳定的,但需要额外的存储空间(O(n)级别)。
#include <iostream> #include <algorithm> #include <string> #include <algorithm> #include "SortTestHelper.h" //将arr[l..mid]和arr[mid+1...r]两部分进行归并 template<typename T> void _merge(T arr[], int l, int mid, int r){ T *aux = new T[r-l+1]; int right = mid + 1; int tmpIndex = 0; int left = l; //归并内部用插排把元素一个一个塞进辅助数组 while(l <= mid && right <= r){ if(arr[l] <= arr[right]){ aux[ tmpIndex++ ] = arr[ l++ ]; }else{ aux[ tmpIndex++ ] = arr[ right++ ]; } }
//特殊对待一边已经遍历完,另一边还剩一组序列的元素 if(left == mid+1){ while(right <= r) aux[ tmpIndex++ ] = arr[ right++ ]; }else{ while(l <= mid) aux[ tmpIndex++ ] = arr[ left++ ]; } //再循环把辅助数组的元素覆盖进原数组 for(left = l, tmpIndex = 0;left <= r; left++, tmpIndex++) arr[left] = aux[tmpIndex]; //释放辅助数组的存储空间 delete []aux; } template<typename T> void segment(T arr[], int l, int r ){ //递归方式首先就是写递归出口 if( l >= r ) return; //解决l+r两个大整数相加会整数溢出的情况 //int mid = (l+r)/2; int mid = (r-l)/2+l; segment(arr, l, mid); segment(arr, mid+1, r); if( arr[mid] > arr[mid+1] ) //优化归并排序,排除不必要的归并操作 _merge(arr, l, mid, r); } template<typename T> void mergeSort(T arr[], int n ){ segment(arr, 0, n-1); }
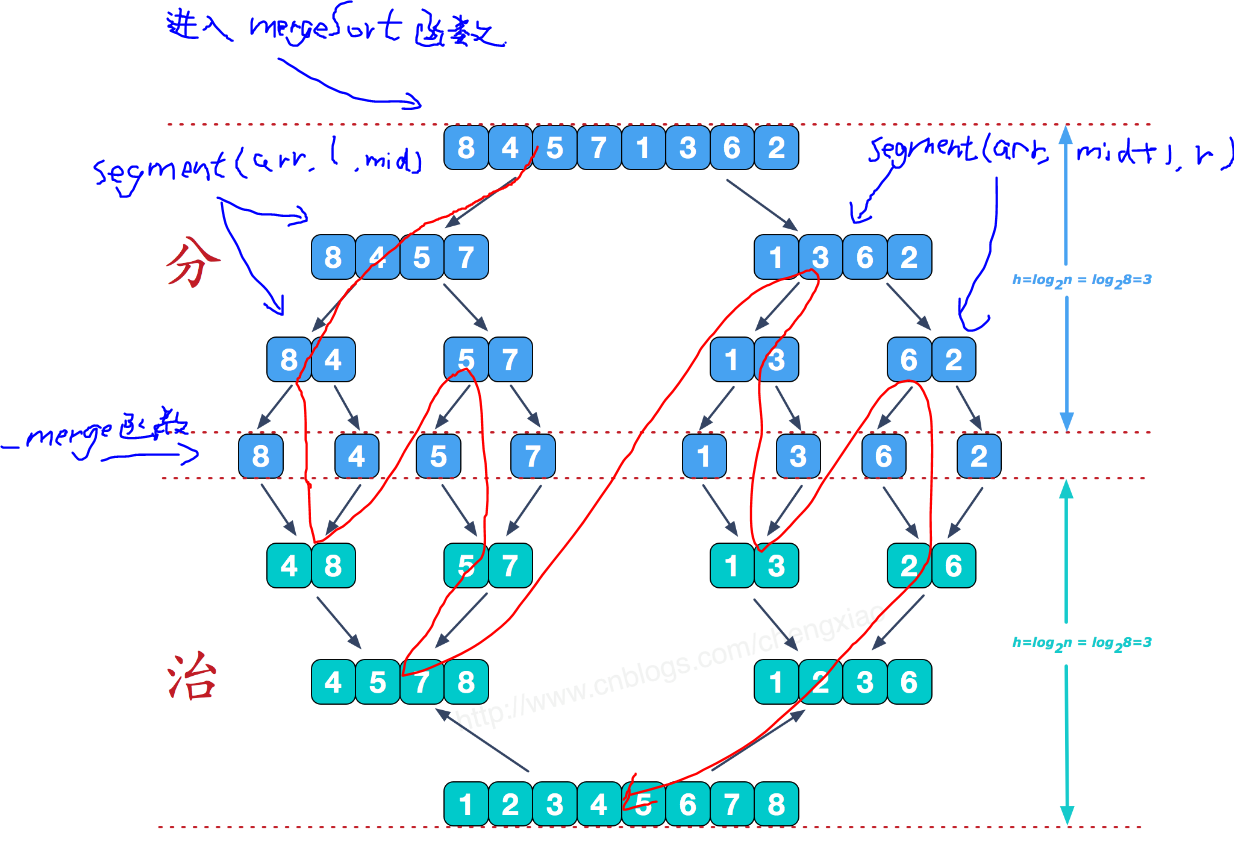
以上是用递归方式自顶向下并初步优化了的归并排序实现代码,总体思路就是主程序从mergeSort函数调用归并排序,在segment函数中进行分治,分为几乎等长的两边分别进行递归,最后再调用_merge()进行当前递归层上的左右部分的归并,这里有个小优化,排除了当左边的序列的最大数小于等于右边数列的最小数时的情况,因为此时合并后已经是有序的了,归并内部实现就是利用辅助数组aux[](r-l+1长度的),因左右部分都是有序的,只要利用两个索引和一个辅助数组指针,依次分别遍历左右部分,判断元素大小,并逐个塞进辅助数组aux[]中,完成遍历之后将辅助数组aux[]内部排好序的序列覆盖原数组,并释放辅助数组的空间。
配上图辅助理解(红笔为程序执行顺序,红线下行为进入函数,上行为返回上层递归)配图来源


 浙公网安备 33010602011771号
浙公网安备 33010602011771号