并行排序

排序是一项非常常用的操作，你的应用程序在运行时，可能无时无刻不在进行排序操作。排序的算法有很多，但是对于大部分的算法都是串行执行的。当排序的元素很多时，若使用并行算法代替串行，显然可以更加有效的利用CPU，提高排序效率。但将串行算法修改为并行算法并非易事，甚至会极大的增加原有算法的复杂度。下面介绍几种相对简单的算法。

奇偶交换排序：分离数据相关性

　　在介绍奇偶交换排序前，首先来看一下冒泡排序。在这里，我们将数组从小到大排序：

public static int[] bubbleSort(int[] arr){
        for (int i = 0;i < arr.length - 1;i++){
            for (int j = 0;j < arr.length - 1 - i;j++){
                if (j+1 == arr.length-i){
                    break;
                }
                if (arr[j] > arr[j+1]){
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
        }
        return arr;
    }

　　在冒泡排序的交换过程中，由于每次交换的两个元素存在数据冲突，也就是对于每个元素，它既可能与前面的元素交换，也可能与后面的元素交换，因此很难直接改造成并行算法。如果能够解开这种数据的相关性，就可以比较容易的使用并行算法来实现类似的排序。奇偶交换排序就是基于这种思想的对于奇偶交换来说，它将排序过程分为两个阶段，奇交换和偶交换。对于奇交换来说，它总是比较奇数索引以及相邻的后续元素；偶交换总是比较偶数索引和其相邻的后续元素，并且奇交换和偶交换会成对出现，这样才能保证比较和交换涉及到数组中的每一个元素。

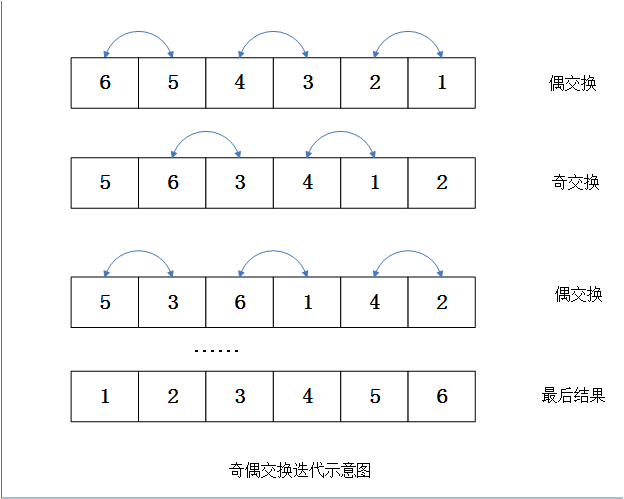
 从上图可以看出，由于将整个比较交换独立分割为奇阶段和偶阶段。这就使得在每一个阶段内，所有的比较和交换都是没有数据相关性的。因此，每一次比较和交换都可以独立执行，也就可以并行化了。

下面是奇偶交换的串行实现：

public static int[] oddEvevSort(int[] arr){
        int exchFlag = 1,start = 0;
        while (exchFlag == 1 || start == 1){
            exchFlag = 0;
            for (int i = start;i < arr.length - 1;i += 2){
                if (arr[i] > arr[i+1]){
                    int temp = arr[i];
                    arr[i] = arr[i+1];
                    arr[i+1] = temp;
                    exchFlag = 1;
                }
            }
            if (start == 0){
                start = 1;
            }else {
                start = 0;
            }
        }
        return arr;
    }

上述代码中，exchFlag用来记录当前迭代是否发生了数据交换，而start变量用来表示是奇交换还是偶交换。初始时，start为0，表示进行偶交换，每次迭代结束后，切换start状态。如果上一次发生了数据交换，或者当前进行的是奇交换，循环就不会停止，直到程序不再发生交换，并且当前进行的是偶交换为止（表示奇偶交换已经成对出现）。

下面是奇偶交换的并行排序：

public class CurrentOddEven {
    static int[] arr = {23,3,23,4,5,5,6,6,6453,678,68,9,9,79878,97,897897,98,78};
    static int exchFlag = 1;
    static synchronized void setExchFlag(int v){
        exchFlag = v;
    }

    static synchronized int getExchFlag(){
        return exchFlag;
    }
    public static class OddEvenSortTask implements Runnable{
        int i;
        CountDownLatch latch;

        public OddEvenSortTask(int i,CountDownLatch latch){
            this.i = i;
            this.latch = latch;
        }

        @Override
        public void run() {
            if (arr[i] > arr[i+1]){
                int temp = arr[i];
                arr[i] = arr[i+1];
                arr[i+1] = temp;
                setExchFlag(1);
            }
            latch.countDown();
        }
    }

    public static void main(String[] args) throws InterruptedException {
        int start = 0;
        ExecutorService es = Executors.newCachedThreadPool();
        while (getExchFlag() == 1 || start == 1){
            setExchFlag(0);
            //偶数的数组长度，当start=1时，只有length/2-1 个线程
            CountDownLatch latch = new CountDownLatch(arr.length/2-(arr.length%2 == 0?start:0));
            for (int i = start;i < arr.length - 1;i += 2){
                es.submit(new OddEvenSortTask(i,latch));
            }
            //等待所有线程结束
            latch.await();
            if (start == 0){
                start = 1;
            }else {
                start = 0;
            }
        }
        for (int temp:arr){
            System.out.println(temp);
        }
        es.shutdown();
    }
}

 上述代码第11行，定义了奇偶排序的任务类。该任务的主要工作是进行数据的比较和交换（第22~26行）。并行排序的主体在main方法中，使用了countDownLatch来记录线程数量，对于每一次的迭代，使用单独的线程对每一次元素比较和交换操作，在下一次的迭代开始之前，必须等上一次的迭代必须完成。

 希尔排序：改进的插入排序

插入排序也是一种很常见的排序算法。它的基本思想：一个未排序的数组（当然也可以是链表）可以分为两个部分，前半部分是已经排序的，后半部分是未排序的。在进行排序时，只需要在未排序的部分中选择一个元素，将其插入前面有序的数组中即可。最终，未排序的部分会越来越少，直到为0，那么排序就完成了。初始时，可以假设已排序部分就是第一个元素。

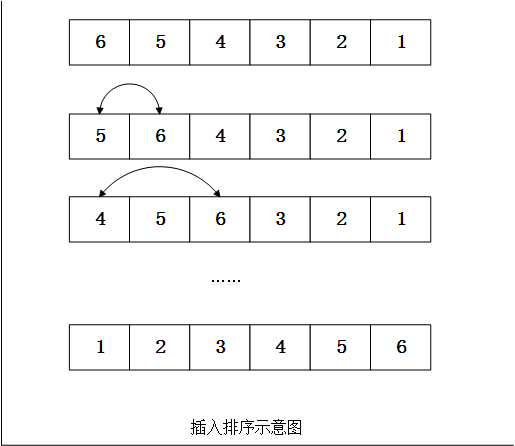
插入排序串行排序如下：

public static int[] insertSort(int[] arr){
        int length = arr.length;
        int i,j,key;
        for (i = 1;i < length;i++){
            //key为要准备插入的元素
            key = arr[i];
            j = i - 1;
            while (j >= 0 && arr[j] > key){
                arr[j+1] = arr[j];
                j--;
            }
            //找到合适的位置插入key
            arr[j+1] = key;
        }
        return arr;
    }

上述代码第6行，提取准备插入的元素（也就是未排序序列中的第一个元素）。接着，在已排序的序列中找到这个元素的插入位置（第8~10行），并进行插入（第13行）即可。

简单的插入排序是很难进行并行化的。因为这一次的数据插入依赖于上一次得到的有序序列，因此多个步骤之间无法并行。为此，我们可以对插入排序进行扩展，就是希尔排序。

希尔排序将整个数组根据间隔h分割为若干个数组。子数组相互穿插在一起，每一次排序时，分别对每一个子数组进行排序。如下图所示（借大神的图侵删）：

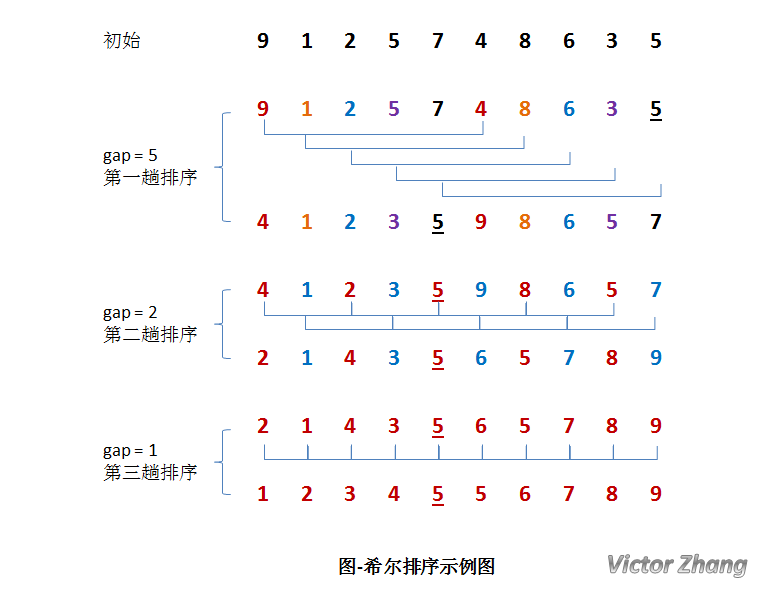
从上图可以看出，每一组排序完成后，可以递减h的值，进行下轮更精细的排序，知道h=1，此时，等价于一次插入排序。

希尔排序的一个主要优点是，即使最小的一个元素在数组的末尾，由于每次元素的移动都以h为间隔进行，因此数组末尾的小元素可以在很少的交换次数下，就被置换到最接近元素最终位置的地方。

下面是希尔排序的串行实现：

public static int[] shellSort(int[] arr){
        //计算出最大的h值
        int h = 1;
        while (h <= arr.length/3){
            h = h*3 + 1;
        }
        while (h > 0){
            for (int i = h;i < arr.length;i++){
                if (arr[i] < arr[i - h]){
                    int temp = arr[i];
                    int j = i - h;
                    while (j >= 0 && arr[j] > temp){
                        arr[j + h] = arr[j];
                        j -= h;
                    }
                    arr[j + h] = temp;
                }
            }
            //计算出下一个h值
            h = (h - 1)/3;
        }
        return arr;
    }

上述代码的4~6行，计算出一个合适的h值，接着进行正式的希尔排序。第8行代码的for循环进行间隔为h的插入排序，每次排序结束后，递减h的值（第20行），直到h=1，退化为插入排序。

由于希尔排序每次都针对不同的子数组进行排序，各个子数组之间是完全独立的，因此，是可以改写为并行程序的：

public class CurrentShellSort {
    static int[] a = {2,3,1,45,53,3,55,4,65,765,7,7,89687,6,89,69,4354,89,99};
    static ExecutorService pool = Executors.newCachedThreadPool();

    public static class ShellSortTask implements Runnable {

        int x = 0;
        int h = 0;
        CountDownLatch l;

        public ShellSortTask(int x, int h, CountDownLatch latch) {
            this.x = x;
            this.h = h;
            this.l = latch;
        }

        public void run() {
            int i, j, key;
            for (i = x + h; i < a.length; i = i + h) {
                if (a[i] < a[i - h]) {
                    j = i - h;
                    key = a[i];
                    while (j >= 0 && a[j] > key) {
                        a[j + h] = a[j];
                        j -= h;
                    }
                    a[j + h] = key;
                }
            }
            l.countDown();
        }
    }

    public static void pShellSort(int[] arr) throws InterruptedException {
        // 计算出最大的n值
        int h = 1;
        CountDownLatch lathc = null;
        while (h <= arr.length / 3) {
            h = h * 3 + 1;
        }
        while (h > 0) {
            System.out.println("h=" + h);
            lathc = new CountDownLatch(h);
            for (int x = 0; x < h; x++) {
                pool.submit(new ShellSortTask(x, h, lathc));
            }
            lathc.await();
            System.out.println(Arrays.toString(arr));
            // 计算下一个h值
            h = (h - 1) / 3;
        }
        pool.shutdown();
    }
    //测试
    public static void main(String[] args) throws InterruptedException {
        pShellSort(a);
    }
}

 输出结果：

h=13
[2, 3, 1, 45, 53, 3, 55, 4, 65, 765, 7, 7, 89687, 6, 89, 69, 4354, 89, 99]
h=4
[2, 3, 1, 4, 53, 3, 7, 7, 65, 6, 55, 45, 4354, 89, 89, 69, 89687, 765, 99]
h=1
[1, 2, 3, 3, 4, 6, 7, 7, 45, 53, 55, 65, 69, 89, 89, 99, 765, 4354, 89687]

 

参考：《Java高并发程序设计》 葛一鸣 郭超 编著：