最大密度子图
最大密度子图
前言
为什么要写这个最大密度子图的介绍呢?
因为一些同学在写博客,不写不好意思了
因为我记不住公式,所以自己推一推
因为这个很重要。能解决很多相关题目。
最大密度子图描绘的一类问题是,给出一张带有点和边的图,其中点和边都有相应权值。请选出一些边和一些点(其中选出的边的两点必须选择),使得边和点的权值与选择的点的个数的比值最大。
这个问题可以用最小割建立联系。在直接建图前,先推导一下。
推理过程
我们以下面的图为例子。其中v是边权,w是点权。
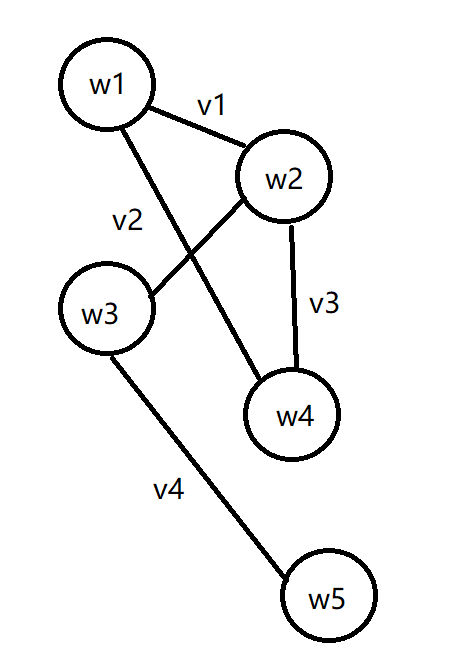
当然这个图的点和边比较少,这是方便画图举例子。
首先推导一下公式。我们假设G是原图,|E|是我们选择的边权的值的总和,V是我们选择的子图,|V|是选择的点权的和,|P|是选择的点的个数。
那我们只需让这个式子最大:

不妨设这个式子的值为g,即

我们的目的便是让g取最大值。那我们对式子稍作整理。
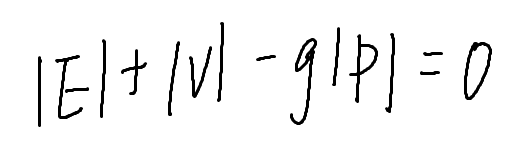
如果我们计算出左式最大值要大于0,那么说明我们的g取得过小;如果我们计算出左式最大值要小于0,那么说明我们的g取得过大
竞赛中,我们可以通过这边可以启发我们,通过二分枚举g的值,直到取出来一个g,使得左边的式子等于0。
那接下来,我们需要求出来|E| + |V| - g|P|的最大值。
不妨转换思路,求一下g|P| - |E| - |V|的最小值。
而上述式子不太好计算,我们可以进行相关的式子整理。其中V'表示G - V,即原图中V之外的部分,P表示某个点,v表示边权,w表示点权。
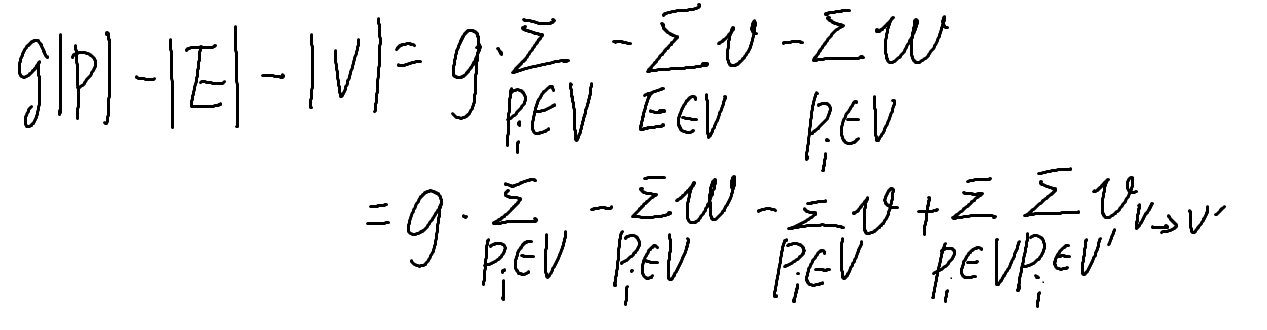
其中式子里的g是我们枚举出来的,算是一个已知量;w是点权,v是边权,都是已知量。那我们接下来求这个式子的最小值。
这里有一个很取巧的方式。我们可以把一条边的权值都加到两个点上,这样在计算相关值时只需用点的相关值去计算,而不是需要枚举边。不过这样算出来的值应该减半,因为两个点都被增加了一次。
这样相应的式子会变换为如下形式,其中d表示点所连接的边的权值。
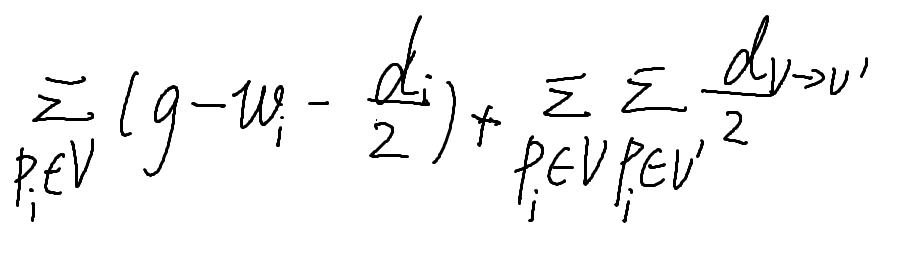
不过带有分母不太好看,我们把分母提到整个式子之前,让式子好看一些。
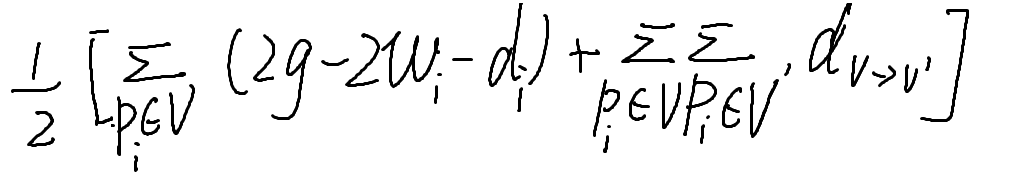
哎,注意到这个东西。

两个没有交集的子图的并集是原图,取的边是两个子图之间的边,这和割十分相似!
因此,我们尝试用割解决这个问题。我们将原式变换一下形式,能美观不少。其中c表示割。

确实美观太多了
既然求上述式子的最小值,我们能够求出来每个点的w和d,我们可以枚举g,那怎么将相关问题和割建立联系呢?
这里有一种神奇的建图方式。我们维持原图不变,设立一个虚拟源点和虚拟汇点,每个点向汇点连一条容量为2g - 2w - d的边。考虑到这个值可能能是负的,我们取一个比较大的值U,改为向汇点连一条容量U + 2g - 2w - d的边。为了弥补这一流量,我们再从虚拟源点向每一个点连一条容量为U的边。其中,w和d的值与所选点相关,g是枚举的值。

那我们求一下这个图的割。我们记源点为s,和源点在割的同一侧的其他点为V;源点为t,和源点在割的同一侧的其他点为V'.其中的V和V'与上面的V和V'是对应的。
我们注意到割由以下四部分组成:
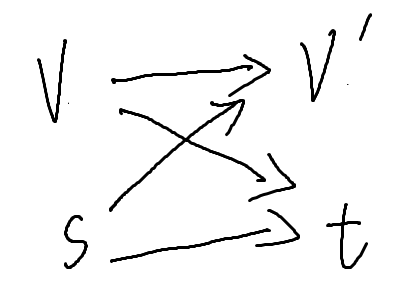
在这种建图方式下,没有从s流向t的流量边。只需计算其他三项。那我们可以计算割,列式如下,其中的S表示{s} + V, T表示{t} + V':
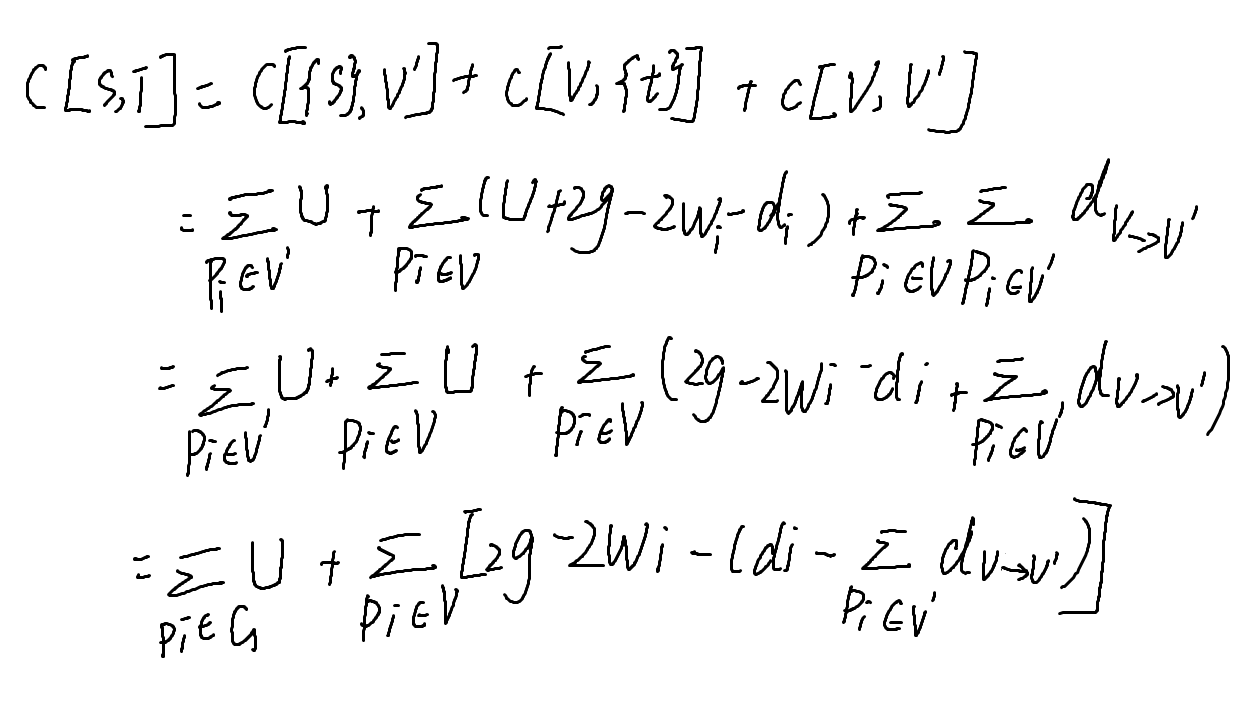
我们惊奇的发现这样一个部分:
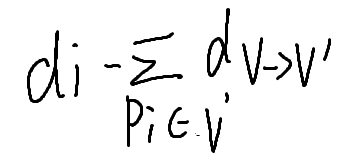
所选子图内的点所连所有边的权值减去子图内点与所选子图外点所连边的权值,正是子图内部所有边的权值!不过由于上述处理,这里的值是原图权值的2倍,即2|E|.继续整理,化简可得下列式子,其中n是原图G所有点的个数。
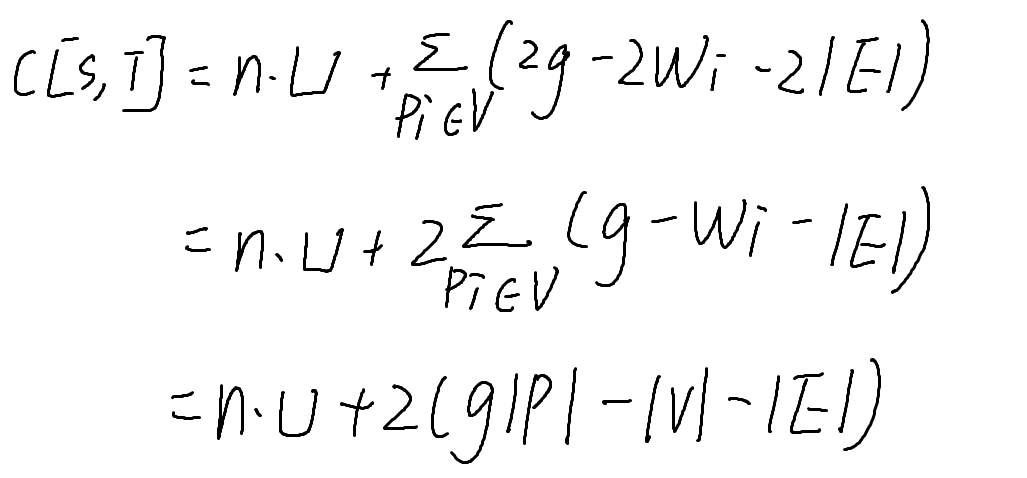
哎,看见了眼熟的东西。

这个g|P| - |V| - |E|,正是我们上述想要求的式子的最小值!
那我们整理以下,可得
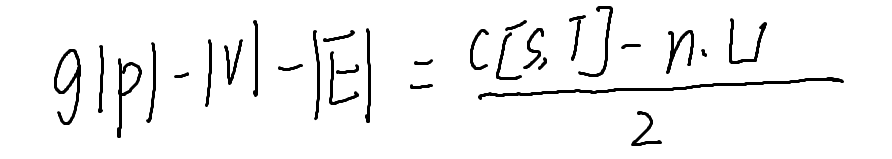
其中,n与U为定值,要使式子值最小,只需让c[S, T]最小,即求一个最小割。
原来我们求的值是|E| + |V| - g|P|的最大值, 其所对应的值是(n * U - c[S, T])/ 2, 仍然可以求最小割来解决。
那么我们通过二分g的值,再通过如上的建图方式,便可以通过最小割将值求出,进而缩小g的范围,求出答案。
原式 |E| + |V| - g|P| 的值即 n * U - c[S, T] 的值小于0时,说明g不够大,需要将左边界提高;大于0时,说明g过大,需要压低右边界。
那么,如何将建图后的结果与原问题一一对应呢?
我们注意到在上述建图中,选择的V与V'与原问题的V和V'一致,那么在原问题中选择的点,便在新图中与s处于同一个集合,这样二者的对应性也找到了。
总结
最大密度子图的解决方式可以用如上建图方式解决。除了竞赛中考察,现实生活中也有许多可用之处。可惜的是不少现实生活中的问题不能二分答案了,目前没有想到好的解决方案,或许只能一一枚举答案了吧。
这里没有代码是因为我懒了



