斐波那契数列

1.斐波那契数列

斐波那契数列是如下的数列:1, 1, 2, 3, 5, 8, 13...

其中，该数列的前两项是1，从第三项（包括第三项）开始第n项为第（n - 1）项与第（n - 2）项的和。

2.斐波那契数列递推公式

斐波那契数列的递推公式比较显然。斐波那契数列第n（n > 2）项的值【记作Fib(n)】为

Fib(n) = Fib(n - 2) + Fib(n - 1)

特殊地，若n为1或者2，那么Fib(n) = 1.

3.C语言代码递推实现

#include<stdio.h>

long long int Fibnacci(long long int n);

int main(){
　　long long int n;
　　scanf("%lld", &n);
　　printf("%lld", Fibnacci(n));
　　printf("\n");
　　return 0;
}

long long int Fibnacci(long long int n){
　　if(n == 1 || n == 2){
　　　　return 1;
　　}
　　else if(n > 2){
　　　　return (Fibnacci(n - 1) + Fibnacci(n - 2));
　　}
return 0;
}

看得出来代码比较整洁。

实际运行时：

 

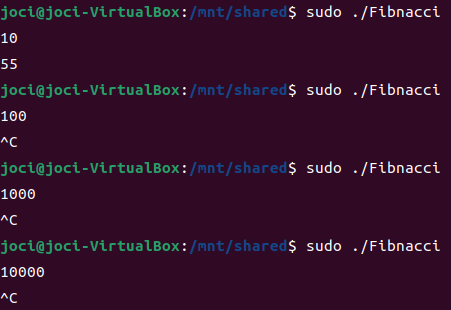
 只有Fib(10)能够比较快的运算出来。算100及以上的数字时花费了不少时间仍未结果，只能强行停止程序。

果然计算机不喜欢跑递归程序。

用数组循环等方式可以解决时间问题，速度比较快。

4.栈的状况

程序在调用函数时便会生成栈。

 

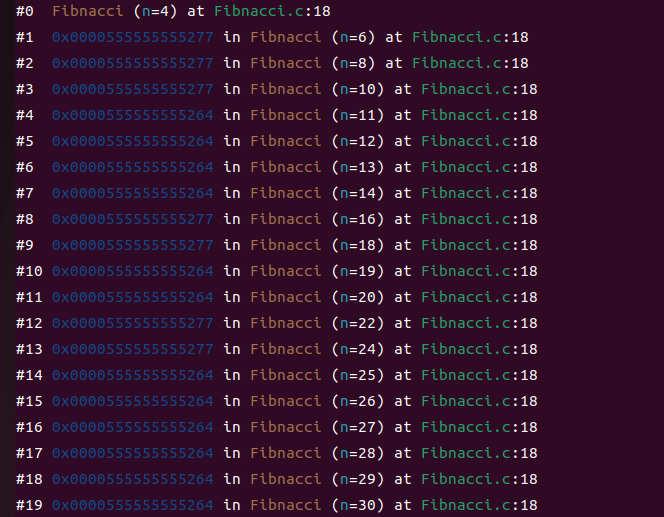
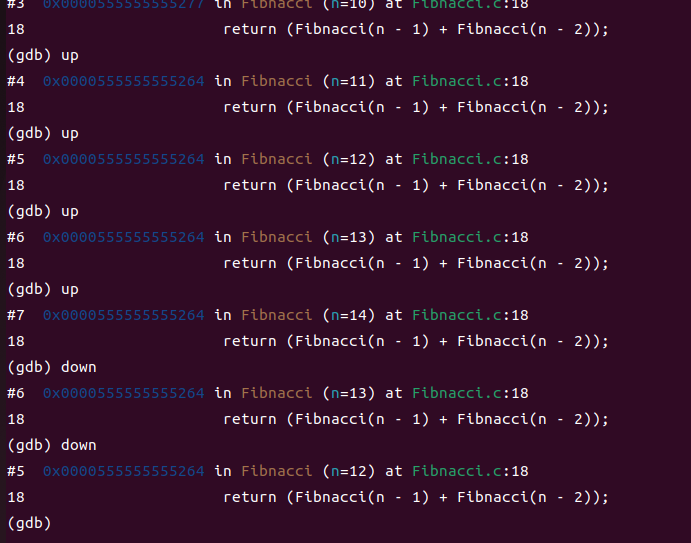
 以上时个人在输入100时的栈的状况，一小段时间后强行停止输出栈的状况才到30.看来计算机真的很不喜欢递归。