RSA脚本环境配置-攻防世界-OldDriver

【Crypto】 题目链接 【RSA算法解密】
⭐审题分析⭐
首先拿到一个压缩包,解压得到文件enc.txt。 先不用去管其他,第一眼enc马上联想到 RSA解密。接着往下看
[{"c": 7366067574741171461722065133242916080495505913663250330082747465383676893970411476550748394841437418105312353971095003424322679616940371123028982189502042, "e": 10, "n": 25162507052339714421839688873734596177751124036723831003300959761137811490715205742941738406548150240861779301784133652165908227917415483137585388986274803},
{"c": 21962825323300469151795920289886886562790942771546858500842179806566435767103803978885148772139305484319688249368999503784441507383476095946258011317951461, "e": 10, "n": 23976859589904419798320812097681858652325473791891232710431997202897819580634937070900625213218095330766877190212418023297341732808839488308551126409983193},
{"c": 6569689420274066957835983390583585286570087619048110141187700584193792695235405077811544355169290382357149374107076406086154103351897890793598997687053983, "e": 10, "n": 18503782836858540043974558035601654610948915505645219820150251062305120148745545906567548650191832090823482852604346478335353784501076761922605361848703623},
{"c": 4508246168044513518452493882713536390636741541551805821790338973797615971271867248584379813114125478195284692695928668946553625483179633266057122967547052, "e": 10, "n": 23383087478545512218713157932934746110721706819077423418060220083657713428503582801909807142802647367994289775015595100541168367083097506193809451365010723},
{"c": 22966105670291282335588843018244161552764486373117942865966904076191122337435542553276743938817686729554714315494818922753880198945897222422137268427611672, "e": 10, "n": 31775649089861428671057909076144152870796722528112580479442073365053916012507273433028451755436987054722496057749731758475958301164082755003195632005308493},
{"c": 17963313063405045742968136916219838352135561785389534381262979264585397896844470879023686508540355160998533122970239261072020689217153126649390825646712087, "e": 10, "n": 22246342022943432820696190444155665289928378653841172632283227888174495402248633061010615572642126584591103750338919213945646074833823905521643025879053949},
{"c": 1652417534709029450380570653973705320986117679597563873022683140800507482560482948310131540948227797045505390333146191586749269249548168247316404074014639, "e": 10, "n": 25395461142670631268156106136028325744393358436617528677967249347353524924655001151849544022201772500033280822372661344352607434738696051779095736547813043},
{"c": 15585771734488351039456631394040497759568679429510619219766191780807675361741859290490732451112648776648126779759368428205194684721516497026290981786239352, "e": 10, "n": 32056508892744184901289413287728039891303832311548608141088227876326753674154124775132776928481935378184756756785107540781632570295330486738268173167809047},
{"c": 8965123421637694050044216844523379163347478029124815032832813225050732558524239660648746284884140746788823681886010577342254841014594570067467905682359797, "e": 10, "n": 52849766269541827474228189428820648574162539595985395992261649809907435742263020551050064268890333392877173572811691599841253150460219986817964461970736553},
{"c": 13560945756543023008529388108446940847137853038437095244573035888531288577370829065666320069397898394848484847030321018915638381833935580958342719988978247, "e": 10, "n": 30415984800307578932946399987559088968355638354344823359397204419191241802721772499486615661699080998502439901585573950889047918537906687840725005496238621}]
给出 十组RSA(enc)加密信息。且十组的e都相同。这里涉及到三个参数:
e / c :c要满足 : e * c = 1 (mod(p-1) * (q-1))
n : n = p * q(p和q是两个不同的大素数)
{ e , n } 为公开密钥 { c , n } 为私有密钥
详情可参考 阮一峰RSA算法
⭐低加密指数广播攻击⭐
推一波大佬的总结: 详情戳这里
低加密指数广播攻击
介绍:
如果选取的加密指数较低,并且使用了相同的加密指数给一个接受者的群发送相同的信息,那么可以进行广播攻击得到明文。即,选取了相同的加密指数e(这里取e=3),对相同的明文m进行了加密并进行了消息的传递,那么有:
$ c_1equiv m^e$ $mod$ $n_1$
$ c_2equiv m^e$ $mod$ $n_2$
$ c_3equiv m^e$ $mod$ $n_3$
对上述等式运用中国剩余定理,在e=3时,可以得到:
$ c_xequiv m^3$ $mod$ $n_1n_2n_3$
通过对$ c_x $进行三次开方可以求得明文。
识别:
这个识别起来比较简单,一般来说都是给了三组加密的参数和明密文,其中题目很明确地能告诉你这三组的明文都是一样的,并且e都取了一个较小的数字。
⭐环境准备⭐
-
python2.x -- python3.x环境准备 -
libnum
-
gmpy2(重头戏)
python2.x -- python3.x 环境准备
第一个相信大家都已经准备好了。
安装 libunm
如何下载 libunm库 只需打开 cmd 窗口,执行该命令即可:
pip install libnum -i https://pypi.mirrors.ustc.edu.cn/simple/
-i 后面接的是镜像源,加速下载。 可以换源 自取。
阿里云 http://mirrors.aliyun.com/pypi/simple/
中国科技大学 https://pypi.mirrors.ustc.edu.cn/simple/
豆瓣(douban) http://pypi.douban.com/simple/
清华大学 https://pypi.tuna.tsinghua.edu.cn/simple/
中国科学技术大学 http://pypi.mirrors.ustc.edu.cn/simple/
若是下载失败或者在pycharm里运行还是显示没有该模块,则我们可以采取直接法。直接在pycharm里下载该库。
先打开pycharm -> settings -> Project Interpreter -> "+" -> 输入 libnum ->下载 -> 完成。

这里提一句: 点击下方红框按钮,进行添加镜像,下载速度会更快哦~镜像源在上面已经给出,可自取!
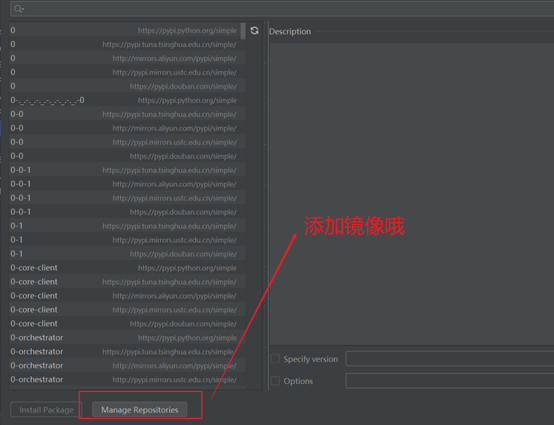
若出现 不信任报错,手动修改 http 为 https 即可!
顺带一提:在做RSA解题时经常会碰到 import crypto 如题【攻防世界】 cr3-what-is-this-encryption
import libnum
from Crypto.Util.number import long_to_bytes
安装pycryptodome
缺少crypto模块怎么办?
法一: pip 安装
法二: pycharm 里直接安装 crypto ,发现找不到?! 实际上应安装
pycrypto即可。(法一法二均与上述libnum模块安装一致)
法三:pycharm里面直接安装
pycryptodome模块(PS:像博主这种倒霉蛋pycrypto又没安成功,只好曲线救国)
这样就万事大吉啦~~
Windows下 -- gmpy2安装
最后一项 下载 gmpy2库 这可真是太折腾了。 博主亲测:
-
第一种:与上述装 libnum库 一样,直接 pip 或者 pycharm 里安装 。 (反正倒霉蛋我是不行的)
-
第二种:利用pip 安装 .whl 轮子文件 成功上岸!!
首先,确定自己的python 版本 ,可直接 用
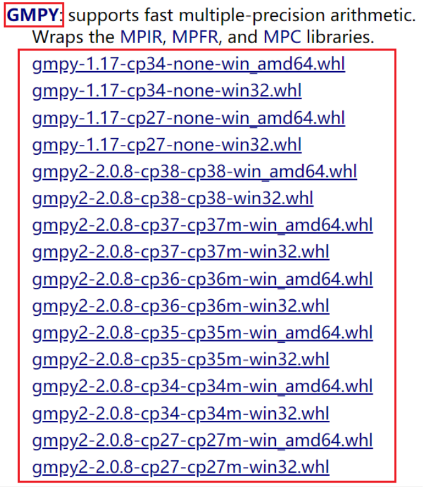
python -version查看。下面,来这个 宝藏之地 找到
GMPY板块。 根据自己的python版本来进行相应的下载。比如说,博主的python环境是 python3.8 ,并且,电脑是64版本,那就下载相对应的
gmpy2‑2.0.8‑cp38‑cp38‑win_amd64.whl的文件 即可。
安装后,进入你安装的python环境的目录。打开
Script文件夹,将刚下载好的.whl文件拖进去,然后在此处打开 cmd窗口 ,或者是 Powershell 。 执行以下命令 : 注意!!.whl文件名一定要复制完整!!
C:\Program Files\Python38\Scripts> pip install gmpy2‑2.0.8‑cp38‑cp38‑win_amd64.whl这样就安装成功啦!!
Kali Linux下安装 RsaCtfTools
RsaCtfTools 也是解Rsa题目的必备神器。 如何安装,大家可以康康大佬的这篇 kail下安装RsaCtfTool
(博主亲测安装很顺利)
但是!! 在安装mpfr时 ,记得将命令换成这条哦!不然会404
wget https://www.mpfr.org/mpfr-current/mpfr-4.1.0.tar.bz2在执行
pip install -r requirements.txt时,记得 先返回 RsaCtfTool目录中哦cd ../ cd ../友情提醒一下 RsaCtfTool.py 是 python3 哒
python2 pip 安装 :
apt-get install python-pippython3 pip3 安装 :
apt-get install python3-pip
python -V查看当前版本~
Successful!!!
⭐解题脚本⭐
python3.x 脚本
import libnum
import gmpy2
dic =[{"c":7366067574741171461722065133242916080495505913663250330082747465383676893970411476550748394841437418105312353971095003424322679616940371123028982189502042, "e": 10, "n":25162507052339714421839688873734596177751124036723831003300959761137811490715205742941738406548150240861779301784133652165908227917415483137585388986274803},
{"c":21962825323300469151795920289886886562790942771546858500842179806566435767103803978885148772139305484319688249368999503784441507383476095946258011317951461, "e": 10, "n":23976859589904419798320812097681858652325473791891232710431997202897819580634937070900625213218095330766877190212418023297341732808839488308551126409983193},
{"c":6569689420274066957835983390583585286570087619048110141187700584193792695235405077811544355169290382357149374107076406086154103351897890793598997687053983, "e": 10, "n":18503782836858540043974558035601654610948915505645219820150251062305120148745545906567548650191832090823482852604346478335353784501076761922605361848703623},
{"c":4508246168044513518452493882713536390636741541551805821790338973797615971271867248584379813114125478195284692695928668946553625483179633266057122967547052, "e": 10, "n":23383087478545512218713157932934746110721706819077423418060220083657713428503582801909807142802647367994289775015595100541168367083097506193809451365010723},
{"c":22966105670291282335588843018244161552764486373117942865966904076191122337435542553276743938817686729554714315494818922753880198945897222422137268427611672, "e": 10, "n":31775649089861428671057909076144152870796722528112580479442073365053916012507273433028451755436987054722496057749731758475958301164082755003195632005308493},
{"c":17963313063405045742968136916219838352135561785389534381262979264585397896844470879023686508540355160998533122970239261072020689217153126649390825646712087, "e": 10, "n":22246342022943432820696190444155665289928378653841172632283227888174495402248633061010615572642126584591103750338919213945646074833823905521643025879053949},
{"c":1652417534709029450380570653973705320986117679597563873022683140800507482560482948310131540948227797045505390333146191586749269249548168247316404074014639, "e": 10, "n":25395461142670631268156106136028325744393358436617528677967249347353524924655001151849544022201772500033280822372661344352607434738696051779095736547813043},
{"c":15585771734488351039456631394040497759568679429510619219766191780807675361741859290490732451112648776648126779759368428205194684721516497026290981786239352, "e": 10, "n":32056508892744184901289413287728039891303832311548608141088227876326753674154124775132776928481935378184756756785107540781632570295330486738268173167809047},
{"c":8965123421637694050044216844523379163347478029124815032832813225050732558524239660648746284884140746788823681886010577342254841014594570067467905682359797, "e": 10, "n":52849766269541827474228189428820648574162539595985395992261649809907435742263020551050064268890333392877173572811691599841253150460219986817964461970736553},
{"c":13560945756543023008529388108446940847137853038437095244573035888531288577370829065666320069397898394848484847030321018915638381833935580958342719988978247, "e": 10, "n":30415984800307578932946399987559088968355638354344823359397204419191241802721772499486615661699080998502439901585573950889047918537906687840725005496238621}]
n = []
C = []
for i in dic:
n.append(i["n"])
C.append(i["c"])
N = 1
for i in n:
N *= i
Ni = []
for i in n:
Ni.append(N // i)
T = []
for i in range(10):
T.append(int(gmpy2.invert(Ni[i], n[i])))
X = 0
for i in range(10):
X += C[i] * Ni[i] * T[i]
m10 = X % N
m = gmpy2.iroot(m10, 10)
print (libnum.n2s(m[0]))
python2.x 脚本
import libnum
import gmpy2
dic =[{"c":7366067574741171461722065133242916080495505913663250330082747465383676893970411476550748394841437418105312353971095003424322679616940371123028982189502042, "e": 10, "n":25162507052339714421839688873734596177751124036723831003300959761137811490715205742941738406548150240861779301784133652165908227917415483137585388986274803},
{"c":21962825323300469151795920289886886562790942771546858500842179806566435767103803978885148772139305484319688249368999503784441507383476095946258011317951461, "e": 10, "n":23976859589904419798320812097681858652325473791891232710431997202897819580634937070900625213218095330766877190212418023297341732808839488308551126409983193},
{"c":6569689420274066957835983390583585286570087619048110141187700584193792695235405077811544355169290382357149374107076406086154103351897890793598997687053983, "e": 10, "n":18503782836858540043974558035601654610948915505645219820150251062305120148745545906567548650191832090823482852604346478335353784501076761922605361848703623},
{"c":4508246168044513518452493882713536390636741541551805821790338973797615971271867248584379813114125478195284692695928668946553625483179633266057122967547052, "e": 10, "n":23383087478545512218713157932934746110721706819077423418060220083657713428503582801909807142802647367994289775015595100541168367083097506193809451365010723},
{"c":22966105670291282335588843018244161552764486373117942865966904076191122337435542553276743938817686729554714315494818922753880198945897222422137268427611672, "e": 10, "n":31775649089861428671057909076144152870796722528112580479442073365053916012507273433028451755436987054722496057749731758475958301164082755003195632005308493},
{"c":17963313063405045742968136916219838352135561785389534381262979264585397896844470879023686508540355160998533122970239261072020689217153126649390825646712087, "e": 10, "n":22246342022943432820696190444155665289928378653841172632283227888174495402248633061010615572642126584591103750338919213945646074833823905521643025879053949},
{"c":1652417534709029450380570653973705320986117679597563873022683140800507482560482948310131540948227797045505390333146191586749269249548168247316404074014639, "e": 10, "n":25395461142670631268156106136028325744393358436617528677967249347353524924655001151849544022201772500033280822372661344352607434738696051779095736547813043},
{"c":15585771734488351039456631394040497759568679429510619219766191780807675361741859290490732451112648776648126779759368428205194684721516497026290981786239352, "e": 10, "n":32056508892744184901289413287728039891303832311548608141088227876326753674154124775132776928481935378184756756785107540781632570295330486738268173167809047},
{"c":8965123421637694050044216844523379163347478029124815032832813225050732558524239660648746284884140746788823681886010577342254841014594570067467905682359797, "e": 10, "n":52849766269541827474228189428820648574162539595985395992261649809907435742263020551050064268890333392877173572811691599841253150460219986817964461970736553},
{"c":13560945756543023008529388108446940847137853038437095244573035888531288577370829065666320069397898394848484847030321018915638381833935580958342719988978247, "e": 10, "n":30415984800307578932946399987559088968355638354344823359397204419191241802721772499486615661699080998502439901585573950889047918537906687840725005496238621}]
n = []
C = []
for i in dic:
n.append(i["n"])
C.append(i["c"])
N = 1
for i in n:
N *= i
Ni = []
for i in n:
Ni.append(N / i)
T = []
for i in xrange(10):
T.append(long(gmpy2.invert(Ni[i], n[i])))
X = 0
for i in xrange(10):
X += C[i] * Ni[i] * T[i]
m10 = X % N
m = gmpy2.iroot(m10, 10)
print libnum.n2s(m[0])
- python2.x和python3.x环境脚本存在三个不同
Ni.append(N / i)在Python3中,N / i返回的是float类型,float最大值为1.7976931348623157e+308因此会报错OverflowError: integer division result too large for a float所以要将它绕过,用//代替/,这样返回的是Integer。T.append(long(gmpy2.invert(Ni[i], n[i])))在Python3中,不存在long()函数,直接改为int()就可
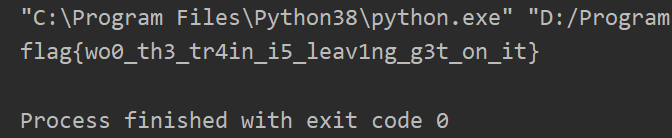
综上!!得到flag啦~~
flag{wo0_th3_tr4in_i5_leav1ng_g3t_on_it}
⭐结语⭐
关于以上链接引用【侵权删】
第一次写博客,多多担待!若有错误之处还请多多指正~!
【转载请放链接】 https://www.cnblogs.com/Jlay/p/RSA_Environment.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号