BUAA_OO U3 Summary
BUAA_OO U3 Summary
架构设计
第一次作业
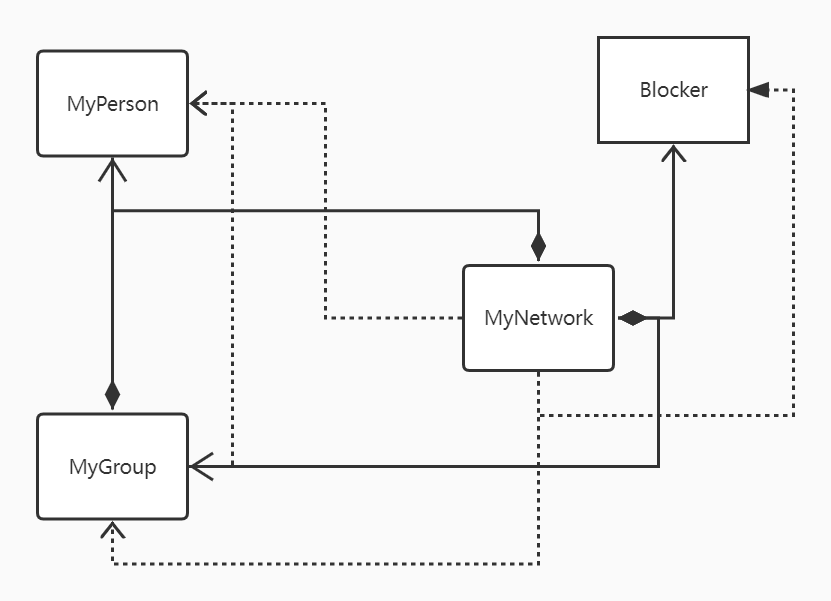
本单元作业以我们数据结构的角度来理解,一个对象Person似一个节点,acquaintance是两个节点之间的权值,Network类是存储了多个连通图的节点图。Group类在本次作业中似乎是一个独立于图外的结构,Group对象相当于给Person对象加了一个从属关系,Group类管理、维护符合从属关系的Person对象的数据(age、acquaintance)之和或是均方差。
所以层次关系也比较明显,所以在Network类和Group类都需要管理Person的对象,而Network中也需要建立对Group对象的管理。
此外,因为需要本次作业涉及连通图的查询,由往年的博客得到启发,决定采用按秩合并优化并查集的算法,为了在实现的类中只包含规格所要求的抽象数据,简化类的实现,所以另建立一个Blocker类,在bloker类中维护节点和边的信息,在访问两个节点是否连通时,也可通过调用bloker类的的接口方法进行查询,从而简化了其余与规格有关的类的实现。
构建图和容器的选择
在Network类以及Group类中,用hashMap管理person类,以ID的key,对应的Person对象为value。这个结构就类似于图中的节点列表。同样的,由于Person类需要管理节点(即Person类间的)连接权值,依据规格的抽象数据,在Person类用HashMap的形式,以对应的连接节点ID为key,对应的连接权值为value建立类似于邻接表的数据规格。
另外值得写一下的就是Blocker类的设计:
Blocker 构建连通图方法
initAddPerson(int id)findFather(int id)merge(int id1, int id2)
Blocker 构建连通图方法
getBlockSum()isCircled(int id1, int id2)
我们可以巧妙地发现,其实Network类就是一个由多个极大连通图组成的社交网络图,blocker类与network类似,只不过,blocker构建图的对外接口只需要person的ID,并且blocker类以构建多叉树的方式构建、管理连通图。
Blocker管理数据如下:
private HashMap<Integer,Integer> fatherMap;
private HashMap<Integer,Integer> rankMap;
private int blockSum;
在本文个人的总结不涉及并查集的具体写法,只结合并查集的写法来具体介绍自己Blocker的设计。当指令需要向Network中add person时,同样需要调用 initAddPerson方法,为Bloker类中加入这个节点的信息,将它的父节点和深度信息进行初始化。此时,还涉及另一个细节上的处理。我们这里需要动态维护最大连通块的个数,这样使后续的查询指令在查询时会比较便利。我们可以认为,加入一个新的Person节点时,即是加入一个与当前节点都不连通的节点,所以连通块的个数需要加1。
当Network需要add relation方法时,我们同样需要调用Blocker的merge()接口方法,merge方法即把id1所属连通图的根节点,id2所属连通图的根节点进行合并,因为我们可以认为,只需要id1与id2建立关系,id1原连通图中的任意节点都与id2原连通图中的任意节点是可到达的。**此时,需要对极大连通快的操作进行减1操作**。
第二次作业
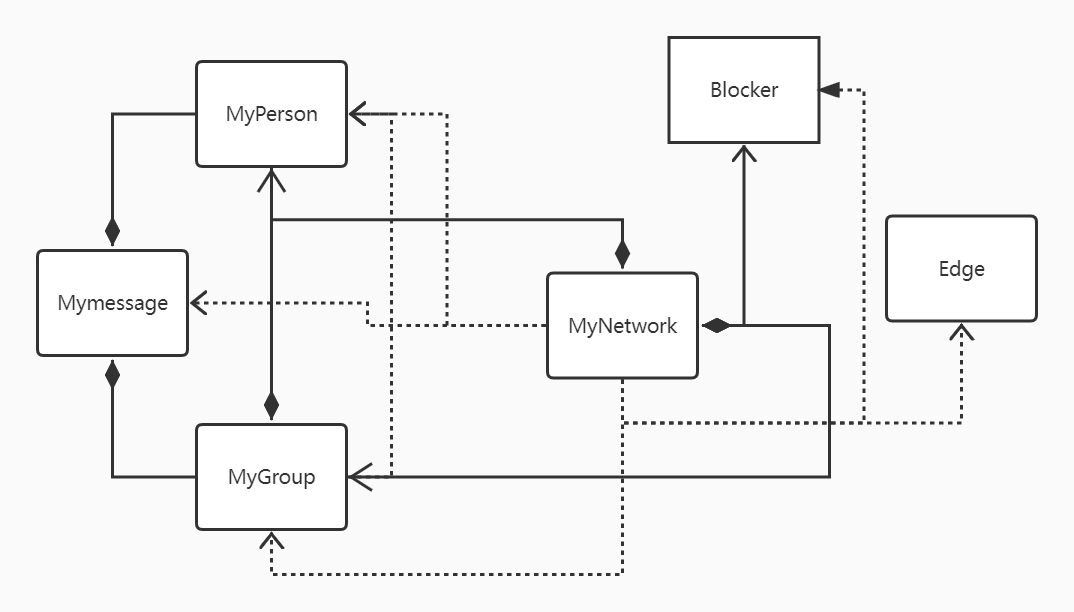
第二次作业引入了Message类以及在Network的算法中涉及了最小生成树的构建。整体构建仍是以Hashmap,Id索引各个Message元素的查找。
作业中最小生成树的算法,我采用Prim+堆优化的算法,堆优化的实现则使用了PriorityQueue,PriorityQueue类中add接口和poll接口可以自行实现堆的维护和和对堆顶的读取。为了便于实现优先队列优先级的定义,我在本作业新建了一个Edge类,存储对应的节点Id和value权值数据,重写conmpareTo方法,每次即可从栈顶取出value值最小的节点。
Prim+堆优化代码:
public int queryLeastConnection(int id) throws PersonIdNotFoundException {
if (!people.containsKey(id)) {
throw new MyPersonIdNotFoundException(id);
} else {
int size = blocker.getCirclePeopleNum(id);
if (size == 1) {
return 0;
} else {
int valueSum = 0;
PriorityQueue<Edge> edgeQueue = new PriorityQueue<>();
HashMap<Integer,Integer> visits = new HashMap<>();
HashMap<Integer,Integer> personAcquaintances = people.get(id).getAcquaintance();
for (Integer personId : personAcquaintances.keySet()) {
edgeQueue.add(new Edge(personId, personAcquaintances.get(personId)));
}
visits.put(id,1);
size -= 1;
Edge minEdge;
while (size > 0) {
minEdge = edgeQueue.poll();
while (visits.containsKey(minEdge.getNode())) {
minEdge = edgeQueue.poll();
}
valueSum += minEdge.getValue();
visits.put(minEdge.getNode(),1);
HashMap<Integer,Integer> newAcquaintances =
people.get(minEdge.getNode()).getAcquaintance();
for (Integer personId : newAcquaintances.keySet()) {
if (!visits.containsKey(personId)) {
edgeQueue.add(new Edge(personId, newAcquaintances.get(personId)));
}
}
size -= 1;
}
return valueSum;
}
}
}
第三次作业
第三次作业整体结构与第二次类似,不过需要在方法上需要引入最短路径的算法。我采用的策略是Dijkstra + 堆优化算法。堆实现仍是一个使用PriorityQueue。
Dijkstra + 堆优化:
public int sendIndirectMessage(int id) throws MessageIdNotFoundException
{
if (!containsMessage(id)) {
throw new MyMessageIdNotFoundException(id);
} else if (getMessage(id).getType() == 1) {
throw new MyMessageIdNotFoundException(id);
} else {
Message message = getMessage(id);
if (!blocker.isCircled(message.getPerson1().getId(), message.getPerson2().getId())) {
return -1;
} else {
int id1 = message.getPerson1().getId();
int id2 = message.getPerson2().getId();
PriorityQueue<Node> nodeQueue = new PriorityQueue<>();
HashMap<Integer,Integer> visits = new HashMap<>();
HashMap<Integer,Integer> distance = new HashMap<>();
visits.put(id1,1);
HashMap<Integer,Integer> personAcquaintances = people.get(id1).getAcquaintance();
for (Integer personId : personAcquaintances.keySet()) {
nodeQueue.add(new Node(personId,personAcquaintances.get(personId)));
distance.put(personId,personAcquaintances.get(personId));
}
while (!visits.containsKey(id2)) {
Node miNo = nodeQueue.poll();
while (visits.containsKey(miNo.getNodeId())) {
miNo = nodeQueue.poll();
}
int nowDis = miNo.getDistance();
visits.put(miNo.getNodeId(),1);
HashMap<Integer,Integer> anoAc = people.get(miNo.getNodeId()).getAcquaintance();
for (Integer peoId : anoAc.keySet()) {
if (!visits.containsKey(peoId)) {
if (!distance.containsKey(peoId)) {
distance.put(peoId,(nowDis + anoAc.get(peoId)));
nodeQueue.add(new Node(peoId,(nowDis + anoAc.get(peoId))));
} else {
if (distance.get(peoId) > (nowDis + anoAc.get(peoId))) {
distance.put(peoId,(nowDis + anoAc.get(peoId)));
nodeQueue.add(new Node(peoId,(nowDis + anoAc.get(peoId))));
}
}
}
}
}
Person person1 = message.getPerson1();
Person person2 = message.getPerson2();
person1.addSocialValue(message.getSocialValue());
person2.addSocialValue(message.getSocialValue());
if (message instanceof MyRedEnvelopeMessage) {
person1.addMoney(-((MyRedEnvelopeMessage) message).getMoney());
person2.addMoney(((MyRedEnvelopeMessage) message).getMoney());
} else if (message instanceof MyEmojiMessage) {
int num = emojiHeats.get(((MyEmojiMessage) message).getEmojiId());
emojiHeats.put(((MyEmojiMessage) message).getEmojiId(),(num + 1));
}
person2.getMessages().add(0,message);
deleteMessage(id);
return distance.get(id2);
}
}
}
性能分析
由于在写作业前阅读了大量的往年的博客,吸收了优秀学长学姐们的经验,所以我没有在查询的性能方面被hack住(向往年的学长学姐们致敬)。我们的指令涉及上万条指令,添加的Person对象也有上千的规模,考虑到同一复杂指令的出现可能达到上千次,所以我们的方法中一定不能出现O(n^2)的复杂度。
-
getValueSum:该方法的优化在group类中引入全局变量value,并每次 add Person,delete person, add relation时进行动态维护。 -
getAgeVar()|getAgeMean: 该方法的维护的全局变量为ageSum和ageSqrSum,年龄和和年龄的平方和。\[\sum_{n=1}^N{(a_n - \bar a)^2} = \sum_{n=1}^N{a_n ^ 2} + N \bar a ^2 - 2 * \bar a * \sum_{n=1}^N{a_n} \]用全局变量动态维护年龄和以及平方和,在访询年龄和年龄均方差的复杂度即可降到o(1)。
-
queryBlockSum|isCircle:已在上文构建图中提到,此方法用并查集(按秩合并)优化。 -
queryLeastConnection|sendIndirectMessage:同样,在上文也已提到,用Prim + 堆优化 以及 dijkstra + 堆优化 算法进行性能优化。
测试以及互测分析
本单元的测试中,没有采用Junit单元测试的方式,而选择了采用随机数据测试+对拍的方式对正确性进行验证,和手搓极端数据,加上基于Python评测机对CPU时间的测算,测试方法是否会超出时间的要求。
在数据生成器中,记录了已生成的Person 和 Group的ID,这样可以自由控制正常指令和异常指令的占比。
在第一次的互测阶段,主要的hack点是qbs指令,一些同学如果严格按照规格实现qbs指令,在查询本方法的查询阶段就会产生O(n^2)的复杂度,另外再考虑到调用Iscircle的时间,大量调用qbs指令,如果对方没有使用优化,极容易产生TLE错误,也是基于这样的策略,在第一次作业成功hack到了这个错误。
在第二次的互测阶段,大家都基于第一次作业中的教训,对qbs和qci指令用了并查集的优化,但是第二次作业中出现新的queryValueSum和queryAgeVar的实现都在第一次作业中,但一次作业没有测上述两个指令,有一部分同学在第二次的作业中忽略了对这两个指令的优化。但我并没有hack到queryAgeVar的超时错误,在构造queryValueSum的测试数据时,构造逻辑比较粗暴简单,前1000条指令用于addPerson,1000条指令用于add relation,1000条指令用于add to group,剩余指令全用于query value。
对Network类的扩容
首先在network类中增加对Advertiser,Producer,Customer的抽象数据管理
@ public instance model non_null Advertiser[] advertisers;
@ public instance model non_null Producer[] producers;
@ public instance model non_null Customer[] customers;
1.Network加入发送广告接口
/*@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < advertisers.length; @ advertisers[i].getId() == id1) &&
@ (\exists int i; 0 <= i && i < customers.length; @ customers[i].getId() == id2) &&
@ getadvertiser(id1).hasCustomer(getCustomer(idw)) == false;
@ assignable getadvertiser(id1).Customer;
@ ensures (\forall Customer i; \old(getAdvertiser(id1).hasCustomer(i));
@ getAdvertiser(id1).hasCustomer(i));
@ ensures \old(getAdvertiser(id2).customers.length) == @ getAdvertiser(id2).customers.length - 1;
@ ensures getAdvertiser(id1).hasCustomer(getCustomer(id2)));
@ also
@ public exceptional_behavior
@ signals (AdvertiserIdNotFoundException e) !(\exists int i; 0 <= i && i < @ advertisers.length;
@ advertisers[i].getId() == id1);
@ signals (CustomerIdNotFoundException e) (\exists int i; 0 <= i && i < @ advertisers.length;
@ advertisers[i].getId() == id1) && !(\exists int i; 0 <= i && i < c @ customers.length;
@ customers[i].getId() == id2);
@ signals (EqualAdvertiseException e) (\exists int i; 0 <= i && i < @ advertisers.length;
@ advertisers[i].getId() == id1) && (\exists int i; 0 <= i && i < @ customers.length;
@ customers[i].getId() == id2) && @ getAdvertiser(id1).hasCutomer(getCUstomer(id2));
@*/
public void sendAvertise(int id1, int id2) throws GAdvertiserIdNotFoundException,
CustomerIdNotFoundException, EqualAdvertiseException;
2.查看购物网络内是否连成哈密顿图
/*@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < advertisers.length;
@ advertisers[i].getId() == id)
@ ensures \result == (\exists Customer[] array; array.length == @ getAdvertiser.customer.length;(\forall int i; 0 <= i && i < array.length - @ 1;array[i].isLinked(array[i + 1]) == true)) && (\forall customer i, @ getAdvertiser(id).hascostomer(i);(\exsits int i; 0 <= i && i < @ array.length; i.equals(array[i])))
@ also
@ public exceptional_behavior
@ signals (AdveritiserIdNotFoundException e) !(\exists int i; 0 <= i && i < @ advertisers.length; advertisers[i].getId() == id1);
@ advertisers[i].getId() == id1);
@ signals (CustomerIdNotFoundException e) (\exists int i; 0 <= i && i < @ advertisers.length; advertisers[i].getId() == id1);
@ advertisers[i].getId() == id1) && @ getAdvertiser(id1).customer.length == 0;
@*/
public /*@ pure @*/ boolean isHamilton(int id) throws AdveritiserIdNotFoundException, CustomerIdNotFoundException;
3.消费者发送购买信息
需要在Customer类中加入抽象数据Product[], Producer类中引入销售量
/*@ public normal_behavior
@ requires containsAdvertiser(id1) && containsCustomer(id2) && @ containsProducer(id3)
@ assignable getCostermer(id2).productValue, getCostermer(id2).money;
@ assignable getProducer(id3).sale;
@ ensures \old(getCustomer(is2).money) = getCustomer(is2).money + @ getProducer(id3).price;
@ ensures \old(getCustomer(is2).productValue) = getCustomer(is2).productValue + @ getProducer(id3).productValue;
@ ensures \old(getProducer(id3).sale) == getProducer(id3).sale + @ getProducer(id3).price
@ also
@ public exceptional_behavior
@ signals (ProducerIdNotFoundException e) !containsProducer(id3)
@ signals (AdvertiserIdNotFoundException e) containsProducer(id3) ` @ && !containsAdvertiser(id1)
@ signals (CustomerIdNotFoundException e) containsProducer(id3) ` @ && containsAdvertiser(id1) && containsCustomer(id3)
@*/
public void purchaseProduct(int id1, int id2, int id3) throws AdvertiserIdNotFoundException,CustomerIdNotFoundException,
ProducerIdNotFoundException;
学习体会
本单元学习了如何读取和撰写JML规格,其实学习之初,并不理解JML语言的用处,认为读规格不如读方法的自然语言便捷。但在单元学习之后,总结本单元的学习,才能发现JML“玉韫珠藏”的作用。
回想起前两单元和第四单元第一次作业,尤其是第四单元,我们大多数人在写代码前的在课程群以及讨论区都少不了就各种实现细节向助教询问,实验指导书的自然语言描述的语言也算是细致,但我们仍会产生很多理解上的偏差。如果是在软件行业上,在软件设计测试层次仍在不断向用户询问的实现细节和接口条件,无疑是低效的。我的理解是,规格作为一种契约,是设计层面描述的基于分析用户需求,由用户确认后的最终应实现效果。这样,在设计层面,契约一经确认不载更改,可以极大节省设计细节的讨论,只关注于实现层次。
另外,自身在写JML规格时,其实也是在抽象层次梳理层次逻辑关系,撰写JML规格的层次逻辑有助于我们捋清在实现层面的层次设计。在写完规格撰写后,已经基本列出了满足用户需求的抽象数据和接口,所以我们在设计阶段只需要关注实现抽象数据(例如思考如何选择数据容器),如何准确地实现方法(选择什么算法)。




