《机器学习》第一次作业——第一至三章学习记录和心得
机器学习一到三章笔记
1.1 什么是模式识别
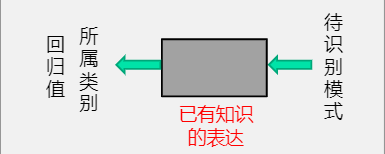
模式识别是根据已有知识表达,针对待识别模式,判别决策其所属的类别或者预测其对应的回归值
本质上是一种推理的过程
1.2 模式识别数学表达
模式识别可以看作一种函数映射f(x),将待识别模式x从输入空间映射到输出空间
- 注意到,f(x)的形式是可解析表达的
- 并且他的输出是确定值、概率值
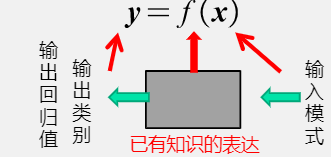
模型:关于已有知识的一种表达方式、即f(x)
- 广义:特征提取+回归器+判别函数
- 狭义:特征提取+回归器
特征:可以用于区分不同类别模式的、可测量的量
特征向量:

1.3 特征向量的相关性
特征向量点积

特征向量投影

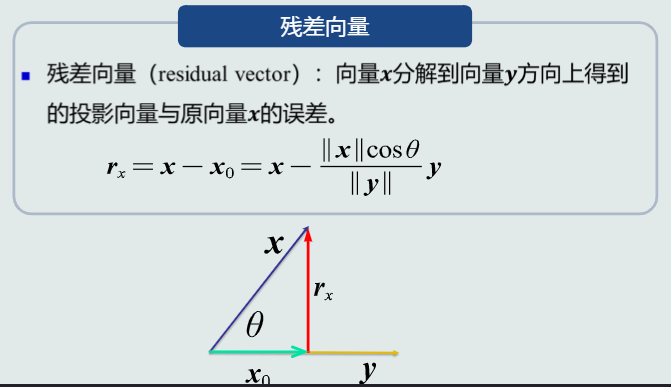
残差向量
1.4机器学习基本概念
模型的参数和结构:

线性模型:模型结构是线性的(直线、面、超平面):y=(W^T)x+W0(w,w0是模型参数)
非线性模型:模型结构非线性:y=g(x),常见非线性模型:多项式、神经网络、决策树
样本量与模型参数量的关系
- N=M:参数有唯一解
- N>>M:没有准确的解(over-determined)
- N<<M:无数个解/无解
目标函数:对于over-determined的情况,需要额外添加一个标准,通过优化该标准来确定一个近似解,这个标准就是目标函数,也叫代价函数或损失函数
优化算法:最小化或最大化目标函数的技术
机器学习方式
- 真值(标签)&标注
- 监督式学习:训练样本及输出真值都给定情况下的机器学习
- 无监督式学习:只给定训练样本,没有给输出真值情况下的机器学习算法
- 半监督式学习:既有标注的训练样本,又有未标注的训练样本情况下的学习算法
1.5 模型的泛化能力
泛化能力:训练得到的模型不仅要对训练样本具有决策能力,也要对新的模式具有决策能力
- 泛化能力低的表现:过拟合
- 如何提高泛化能力:选择复杂度适合的模型,在目标函数中加入正则项
多项式拟合&超参数

1.6 评估方法与性能指标
留出法

K折交叉验证

留一验证

2.1 MED分类器
基于距离的决策:把测试样本到每个类之间的距离作为决策模型,将测试样本判定为与其距离最近的类。
原型的种类:均值——将该类中所有训练样本的均值作为类的原型。最近邻——从一类的训练样本中,选取与测试样本距离最近的一个训练样本,作为该类的原型。
距离的种类:欧式距离,曼哈顿距离,加权欧式距离。
MED分类器:最小欧式距离分类器,类的原型为均值。
import pandas as pd
from sklearn.model_selection import train_test_split
from scipy.spatial.distance import euclidean
import numpy as np
import ai_utils
DATA_FILE = './data_ai_practice/fruit_data.csv'
FRUIT_NAME = ['apple','mandarin','orange','lemon']
FEAT_COLS = ['mass','width','height','color_score']
def get_pred_label(test_sample_feat,train_data):
"""
“近朱者赤” 找最近距离的训练样本,取其标签作为预测样本的标签
"""
dis_lis =[]
for idx,row in train_data.iterrows():
#训练样本特征
train_sample_feat = row[FEAT_COLS].values
#计算距离
dis = euclidean(test_sample_feat,train_sample_feat)
dis_lis.append(dis)
#最小距离对应的位置
pos = np.argmin(dis_lis)
pred_label = train_data.iloc[pos]['fruit_name']
return pred_label
def main():
"""
主函数
"""
#读取数据集
fruit_data = pd.read_csv(DATA_FILE)
#划分数据集
train_data,test_data=train_test_split(fruit_data,test_size=1/5,random_state=10)
#预测对的个数
acc_count = 0
#分类器
for idx,row in test_data.iterrows():
#测试样本特征
test_sample_feat = row[FEAT_COLS].values
#预测值
pred_label = get_pred_label(test_sample_feat,train_data)
#真实值
true_label = row['fruit_name']
print('样本{}的真实标签{},预测标签{}'.format(idx,true_label,pred_label))
if true_label == pred_label:
acc_count += 1
#准确率
accuracy = acc_count/test_data.shape[0]
print('预测准确率{:.2f}%'.format(accuracy*100))
if __name__ == '__main__':
main()
2.2 特征白化
目的:将原始特征映射到一个新的特征空间,使得在新空间中特征的协方差矩阵为单位矩阵,从而去除特征变化的不同及特征之间的相关性
过程:特征转化的过程:将特征转化分为两步:先去除特征之间的相关性(解耦),然后再对特征进行尺度变化(白化)。令W=W1W2,解耦:通过W1实现协方差矩阵对角化,去除特征之间的相关性。白化:通过W2对上一步变换后的特征再进行尺度变换实现所有特征具有相同方差。
2.3 MICD分类器
概念:最小类内距离分类器,基于马氏距离的分类器
- 距离度量:马氏距离
- 类的原型:均值
判别公式
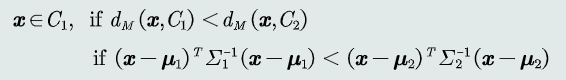
3.1 贝叶斯决策与MAP分类器
后延概率:给定一个测试模式x,决策其属于哪个类别需要依赖于P(Ci|x),该表达式称为后验概率,表达给定模式x属于类Ci的可能性。
贝叶斯规则:要获得后延概率,就要利用贝叶斯规则

MAP分类器:最大后验概率分类器,将测试样本决策分类给后验概率最大的那个类
3.2 MAP分类器:高斯观测概率
表达先验和观测概率的方式
- 常数表达
- 参数化解析表达
- 非参数化表达:直方图,核密度,蒙特卡洛
比较MAP和MICD、MED

3.3 决策风险与贝叶斯分类器
决策风险:不同的错误决策产生完全不一样的风险。
损失:表征当前决策动作相对于其他候选类别的风险程度
决策风险的评估:给定一个测试样本x,分类器决策其属于Ci类的动作对于的决策风险可以定义为相对于所有候选类别的期望损失。
贝叶斯分类器:在MAP分类器基础上,加入决策风险因素,得到贝叶斯分类器。贝叶斯分类器选择决策风险最小的类,即最小化期望损失。
朴素贝叶斯分类器:当特征是多维的,假设特征之间是相互独立的,从而得到以下公式
拒绝选项:当测试数据在决策边界时,即使选择后验概率高的,该概率的值仍然可能很小。为了避免错误决策,引入阈值,当概率低于阈值时不决策
3.4 最大似然估计
定义

3.5 最大似然的估计偏差
无偏估计:如果一个参数的估计量的数学期望是该参数的真值,则估计量称作无偏估计

3.6 贝叶斯估计
贝叶斯估计:给定参数分布的先验概率以及训练样本,估计参数分布的后验概率
高斯观测似然

贝叶斯估计与最大似然估计的对比:贝叶斯估计把参数看作参数空间的一个概率分布,依照训练样本来估计参数的后验概率,从而得到观测似然关于参数的边缘概率,随着样本个数逐渐增大,贝叶斯估计越来越能代表真实的观测似然分布。最大似然估计的参数是确定值,不需要估算参数的边缘概率。
3.7 KNN估计

3.8 直方图与核密度估计





 浙公网安备 33010602011771号
浙公网安备 33010602011771号