201971010116-姜婷 实验二 0/1背包
| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 2022年春软件工程课程班（2019级计算机科学与技术） |
| 这个作业要求链接 | 实验二 软件工程个人项目 |
| 本次课程学习目标 | 1. 掌握git发布软件项目的操作方法 2. 学习使用Python完成背包问题 3. 掌握软件项目个人开发流程 |
| 这个作业在哪些方面帮助我实现学习目标 | 1. 注册并开通了自己的博客，发表第一篇博客 2.注册Github，创建仓库 3. 阅读《现代软件工程—构建之法》，对软件工程有了初步认识 |
任务1：点评班级博客
任务2：总结详细阅读《构建之法》第1章、第2章，掌握PSP流程
第一章 概论
- 软件= 程序 + 软件工程；软件企业 = 软件+商业模式
- 软件开发的不同阶段：
玩具阶段->业余爱好阶段->探索阶段->成熟的产业阶段 - 软件工程是什么？
-
软件工程是把系统的、有序的、可量化的方法应用到软件的开发、运营和维护上的过程。软件工程包括下列领域:软件需求分析、软件设计、软件构建、软件测试和软件维护。
-
软件工程和下列的学科相关:计算机科学、计算机工程、管理学、数学、项目管理学、质量管理、软件人体工学、系统工程、工业设计和用户体验设计。
-
- 软件的特殊性：复杂性、不可见性、易变性、服从性、非连续性。
- 软件工程与计算机科学的关系：
计算机科学中的理论研究部分，大多可以从形式上证明，与数学、离散数学、数理逻辑密切相关;计算机科学中与实践相关的部分，都和数据以及其他学科发生关系;软件工程则和人的行为、现实社会的需求息息相关。软件工程的研究目标（软件的开发、运营和维护）中都有“人”出现，这些“人”可以是项目需求的提供者，可以是软件的开发人员，还可以是软件的用户。 - 软件工程的目标：用户满意度、可靠性、软件流程的质量、可维护性。
第二章 个人技术和流程
- 单元测试标准：
-
单元测试应该在最基本的功能/参数上验证程序的正确性。
-
单元测试必须由最熟悉代码的人（程序的作者)来写。
-
单元测试过后，机器状态保持不变。
-
单元测试要快（一个测试的运行时间是几秒钟,而不是几分钟)。
-
单元测试应该产生可重复、一致的结果
-
独立性——单元测试的运行/通过/失败不依赖于别的测试，可以人为构造数据，以保持单元测试的独立性。
-
单元测试应该覆盖所有代码路径。
-
单元测试应该集成到自动测试的框架中。
-
单元测试必须和产品代码一起保存和维护。
-
- 效能两种分析方法:抽样、代码注入。
- 个人开发流程
-
计划
明确需求和其他相关因素，指明时间成本和依赖关系 -
开发
分析需求
生成设计文档
设计复审
代码规范
具体设计
具体编码
代码复审
测试（包括自测、修改代码、提交修改） -
记录用时
-
测试报告
-
计算工作量
-
事后总结
-
提出过程改进计划
-
- PSP特点：
-
不局限于某一种软件技术（如编程语言)，而是着眼于软件开发的流程。
-
不依赖于考试，而主要靠工程师自己收集数据,然后分析，提高。
-
PSP依赖于数据。
-
PSP的目的是记录工程师如何实现需求的效率。
-
任务3：项目开发
代码规范说明
编码
如无特殊情况, 文件一律使用 UTF-8 编码 如无特殊情况, 文件头部必须加入#--coding:utf-8--标识
代码格式
-
缩进：统一使用 4 个空格进行缩进
-
行宽：每行代码尽量不超过 80 个字符(在特殊情况下可以略微超过 80 ，但最长不得超过 120)
-
引号：简单说，自然语言使用双引号，机器标示使用单引号，因此代码里多数应该使用单引号
-
空行：模块级函数和类定义之间空两行；类成员函数之间空一行；
-
空格：在二元运算符两边各空一格[=,-,+=,==,>,in,is not, and]:
-
换行
- 第二行缩进到括号的起始处
- 第二行缩进 4 个空格，适用于起始括号就换行的情形
-
注释：“#”号后空一格，段落件用空行分开（同样需要“#”号）；作为文档的Docstring一般出现在模块头部、函数和类的头部，这样在python中可以通过对象的__doc__对象获取文档。编辑器和IDE也可以根据Docstring给出自动提示.
-
命名规范
1.模块：模块尽量使用小写命名，首字母保持小写，尽量不要用下划线(除非多个单词，且数量不多的情况)
2.类名：类名使用驼峰(CamelCase)命名风格，首字母大写，私有类可用一个下划线开头
3.函数：函数名一律小写，如有多个单词，用下划线隔开，私有函数在函数前加一个下划线_
4.变量名：变量名尽量小写, 如有多个单词，用下划线隔开；常量采用全大写，如有多个单词，使用下划线隔开
5.常量：常量使用以下划线分隔的大写命名
需求分析
正确读入实验数据文件的有效{0-1}KP数据，并将其处理为便于后续操作的数据形式。
以价值重量为横轴、价值为纵轴的数据散点图
按重量比进行非递增排序。
采用贪心算法求解不超过背包容量的最大价值和解向量。
采用动态规划算法求解不超过背包容量的最大价值和解向量。
采用回溯算法求解不超过背包容量的最大价值和解向量。
最优解、求解时间和解向量可保存为txt文件
功能设计
- 算法运行时间计算，Python3.8不再支持time.clock，用time.perf_counter()替换,分别在算法函数运行前后调用，最终做差计算出运行时间并写入out.txt文件。
点击查看代码
start = time.perf_counter()
end = time.perf_counter()
# 结果写入文件
f = open('out.txt', 'w', encoding='utf-8')
f.write(str(end-start)+ 's'+ '\n')
f.close()
- 写入txt文件，
- 写入excel文件，将之前txt文件中性价比，使用pandas生成excel文件out.xlsx。
点击查看代码
# pip install pandas
import pandas as pd
# 读取文本文件
data = pd.read_csv("out.txt", sep="\t")
data.to_excel("out.xlsx", index=False)
再通过调用openpyxl包实现在excel中指定位置写入物品编号、是否装入。
点击查看代码
设计实现
设计包括你会有哪些类，这些类分别负责什么功能，他们之间的关系怎样？你会设计哪些重要的函数，关键的函数是否需要画出流程图？函数之间的逻辑关系如何？（10分）
测试运行效果及代码实现
- 可正确读入实验数据文件的有效{0-1}KP数据；
点击查看代码
file = 'data\\beibao9.in'
f = open(file, 'r', encoding='utf-8')
- 能够绘制任意一组{0-1}KP数据以价值重量为横轴、价值为纵轴的数据散点图；
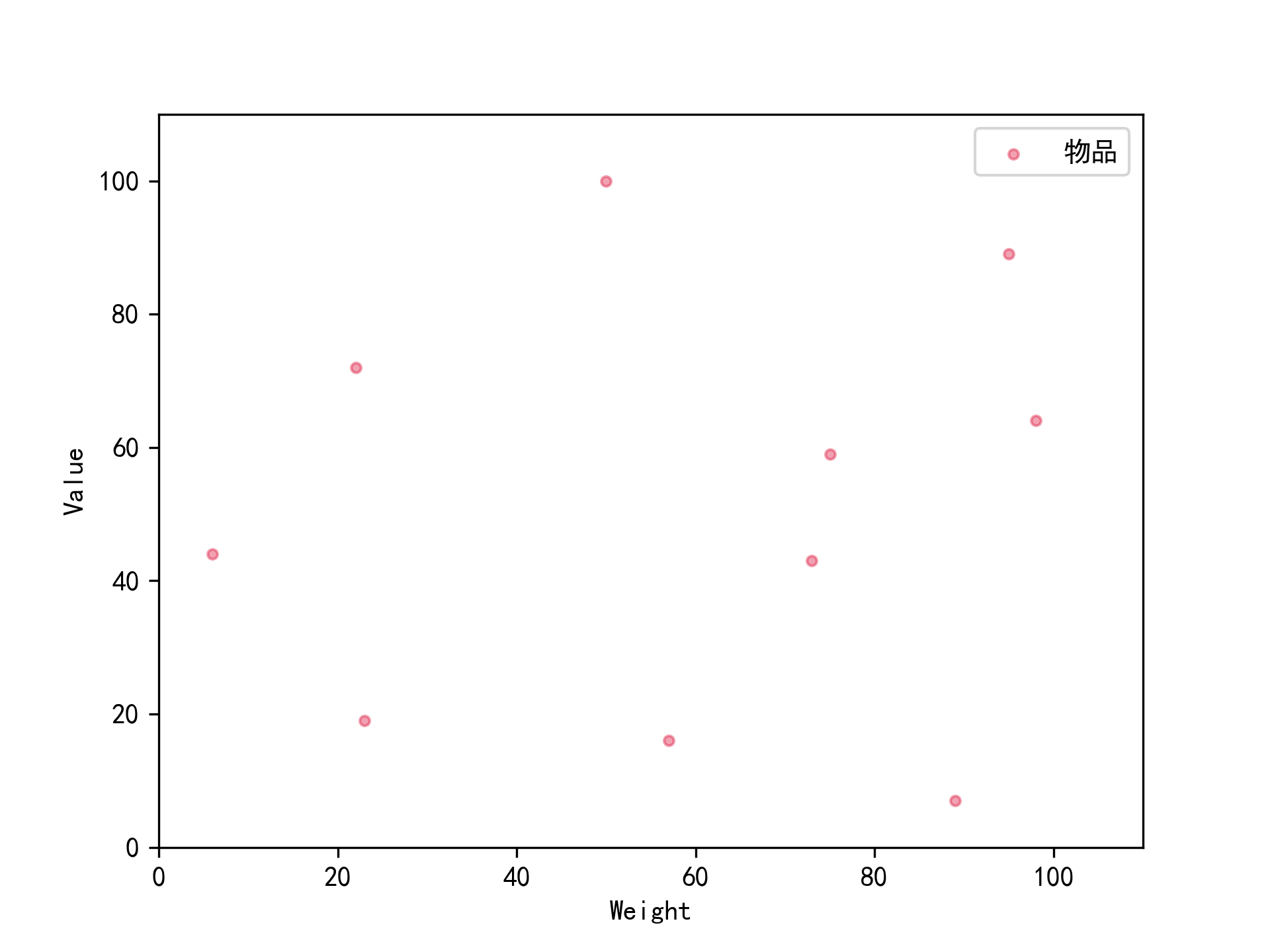
图1 根据beibao2.in数据集画出的散点图
点击查看代码
# 画散点图
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# matplotlib画图中中文显示会有问题，需要这两行设置默认字体
# rcParams用来设置画图时的一些基本参数
# 横轴与纵轴名称及大小
plt.xlabel('Weight')
plt.ylabel('Value')
plt.xlim(xmax=110, xmin=0)
plt.ylim(ymax=110, ymin=0)
# 点的颜色
colors2 = '#DC143C'
# 点面积
area = np.pi * 2 ** 2
plt.scatter(arr_weight, arr_value, s=area, c=colors2, alpha=0.4, label='物品')
plt.legend() # 显示字符或表达式向量
plt.savefig(r'D:\1.png', dpi=300)
plt.show()
- 利用快速排序法实现对一组{0-1}KP数据按重量比进行非递增排序；
图2 非递增排序并显示价值、重量、性价比
点击查看代码
# 快排的主函数，传入参数为一个列表，左右两端的下标
def QuickSort(list, v, w, low, high):
if high > low:
# 传入参数，通过Partitions函数，获取k下标值
k = Partitions(list, v, w, low, high)
# 递归排序列表k下标左侧的列表
QuickSort(list, v, w, low, k - 1)
# 递归排序列表k下标右侧的列表
QuickSort(list, v, w, k + 1, high)
def Partitions(r, v, w, low, high):
i = low
j = high
# 当left下标，小于right下标的情况下，此时判断二者移动是否相交，若未相交，则一直循环
while i < j:
while i < j and r[i] >= r[j]:
j -= 1
if i < j:
temp = r[i]
r[i] = r[j]
r[j] = temp
temp = v[i]
v[i] = v[j]
v[j] = temp
temp = w[i]
w[i] = w[j]
w[j] = temp
i += 1
while i < j and r[i] >= r[j]:
i += 1
if i < j:
temp = r[i]
r[i] = r[j]
r[j] = temp
temp = v[i]
v[i] = v[j]
v[j] = temp
temp = w[i]
w[i] = w[j]
w[j] = temp
j -= 1
return i
- 用户能够自主选择贪心算法、动态规划算法、回溯算法求解指定{0-1} KP数据的最优解和求解时间（以秒为单位）；
- 贪心法
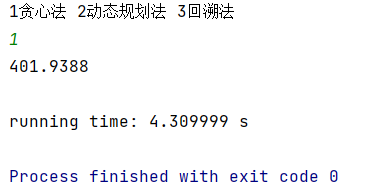
图3 贪心法beibao2.in运行结果
点击查看代码
# 贪心法
def KnapSack(w, v, n, c):
x = [0 for j in range(n+1)]
maxValue = 0
i = 0
for i in range(0, n):
if w[i] < c:
x[i] = 1
maxValue += v[i]
c = c - w[i]
else:
break
x[i] = float(c/w[i])
maxValue += x[i]*v[i]
return maxValue
- 动态规划法
图4 动态规划法贪心法beibao2.in运行结果
点击查看代码
# 动态规划法
def bag(n, c, w, v):
# 置零，表示初始状态
value = [[0 for j in range(c + 1)] for i in range(n + 1)]
for i in range(1, n + 1):
for j in range(1, c + 1):
value[i][j] = value[i - 1][j]
# 背包总容量够放当前物体，遍历前一个状态考虑是否置换
if j >= w[i - 1] and value[i][j] < value[i - 1][j - w[i - 1]] + v[i - 1]:
value[i][j] = value[i - 1][j - w[i - 1]] + v[i - 1]
return value
def show(n, c, w, value):
print('最大价值为:', value[n][c])
x = [False for i in range(n)]
j = c
for i in range(n, 0, -1):
if value[i][j] > value[i - 1][j]:
x[i - 1] = True
j -= w[i - 1]
print('背包中所装物品为:')
for i in range(n):
print(i+1, ' ', end='')
print()
for i in range(n):
if x[i]:
print('1', ' ', end='')
else:
print('0', ' ', end='')
- 回溯法
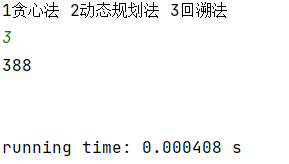
图5 回溯法贪心法beibao2.in运行结果
点击查看代码
# 回溯法
def test(capacity, w, v):
vec_len = 2 ** (len(v) + 1) - 1 # tree `s size
# vec_len = 10000000
vec_v = [0 for j in range(vec_len)]
vec_w = [0 for j in range(vec_len)]
# print(vec_v)
# vec_v = np.zeros(vec_len)
# vec_w = np.zeros(vec_len)
vec_w[0] = capacity
que = queue.Queue()
que.put(0)
best = 0
while (not que.empty()):
current = que.get()
level = int(math.log(current + 1, 2))
if (vec_v[current] > vec_v[best]):
best = current
left = 2 * current + 1 # left child index
right = 2 * current + 2 # right child index
if (left < vec_len and vec_w[current] - w[level] > 0 and vec_v[current] + v[level] > vec_v[best]):
vec_v[left] = int(vec_v[current] + v[level])
vec_w[left] = vec_w[current] - w[level]
que.put(left)
if (right < vec_len and sum(v[level + 1:-1]) + vec_v[current] > vec_v[best]):
vec_v[right] = vec_v[current]
vec_w[right] = vec_w[current]
que.put(right)
# print(vec_w[best], vec_v[best])
print(vec_v[best])
- 任意一组{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
- 结果写入txt文件
图5 动态规划法运行后向out.txt写入运行时间及物品装入情况
点击查看代码
# 结果写入文件
f = open('out.txt', 'w', encoding='utf-8')
f.write('性价比')
f.write('\n')
for i in ratio:
f.write(str(i) + '\n')
f.write(str(end-start)+ 's'+ '\n')
f.close()
data = pd.read_csv("out.txt", sep="\t")
data.to_excel("out.xlsx", index=False)
- 结果写入excel文件
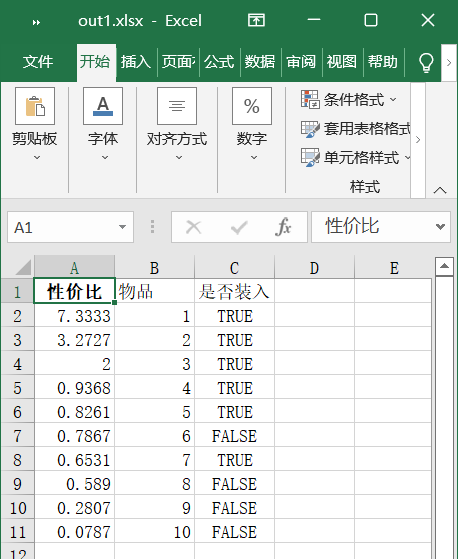
图6 动态规划法运行后分别向out.xlsx写入性价比、物品编号、是否装入
点击查看代码
f = open('out.txt', 'w', encoding='utf-8')
for i in x:
f.write(str(i) + str(x[i])+ '\n')
f.close()
data = pd.read_csv("out.txt", sep="\t")
wb = openpyxl.load_workbook(r'out.xlsx')
ws = wb['Sheet1']
# 取出distance_list列表中的每一个元素，openpyxl的行列号是从1开始取得，所以我这里i从1开始取
ws.cell(row=1, column=2).value ='物品'
ws.cell(row=1, column=3).value ='是否装入'
for i in range(1, len(x) + 1):
distance = x[i - 1]
# 写入位置的行列号可以任意改变，这里我是从第2行开始按行依次插入第3列
ws.cell(row=i + 1, column=3).value = distance
distance = i
ws.cell(row=i + 1, column=2).value = distance
# 保存操作
wb.save(r'out1.xlsx')
总结
此次的项目模块化实现的并不好。仍然将所有的函数以及方法包含在同一个main.py文件当中，代码看起来很长不好搜寻对应的部分。好的软件工程项目应该将相应部分分开存储，未来方便给修改、查询。还有就是回溯算法实现部分并不完善，当数据量较大时对二叉树的存储需求变大，以至于超过python所设置整数的最大容量。对空间效率的思考有欠缺。对于回溯算法部分我应当重新思考，改进代码。
PSP时间分布
| PSP2.1 | 任务内容 | 计划共完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 8 | 10 |
| - Estimate | - 估计这个任务需要多少时间，并规划大致工作步骤 | 8 | 10 |
| Development | 开发 | 600 | 650 |
| - Analysis | - 需求分析（包括学习新技术） | 10 | 8 |
| - Design Spec | - 生产设计文档 | 20 | 25 |
| - Design Review | - 设计复审（和同事审核设计文档） | 8 | 8 |
| - Coding Standard | - 代码规范（为目前的开发指定合适的规范） | 20 | 18 |
| - Design | - 具体设计 | 30 | 25 |
| - Coding | - 具体编码 | 350 | 400 |
| - Code Review | - 代码复审 | 40 | 60 |
| - Test | - 测试（自我测试，修改代码，提交修改） | 120 | 150 |
| Reporting | 报告 | 60 | 62 |
| - Test Report | - 测试报告 | 40 | 35 |
| - Size Measurement | - 计算工作量 | 15 | 10 |
| - Postmortem & Process Improvement Plan | - 事后总结，并提出过程改进计划 | 25 | 25 |
任务4：上传至Gitee
- github上传较慢，多次失败，最终选择将代码上传至gitee实现高效项目托管。
图7 上传至gitee仓库
