POJ 3723 - Conscription ( 最大权森林 / 最小生成树 )

题意

挑选N个女兵，M个男兵，雇佣每个人都需要支付10000元的费用，如果男a和女b存在亲密度d，只要他们其中有一个已经被选中，那么在选另一个人需要的费用为100000-d，给定R个关系，输出一个最低费用，每个关系只能使用一次。

思路

最大权森林转换为负权最小生成树( MST )
当时学最小生成树就这个博客上的图感觉非常好理解:
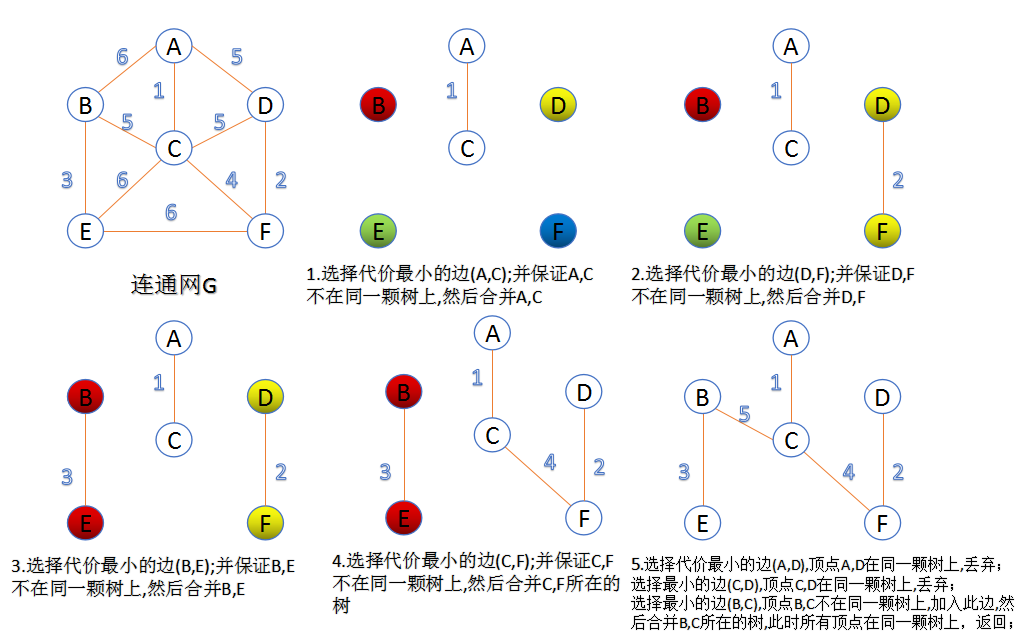
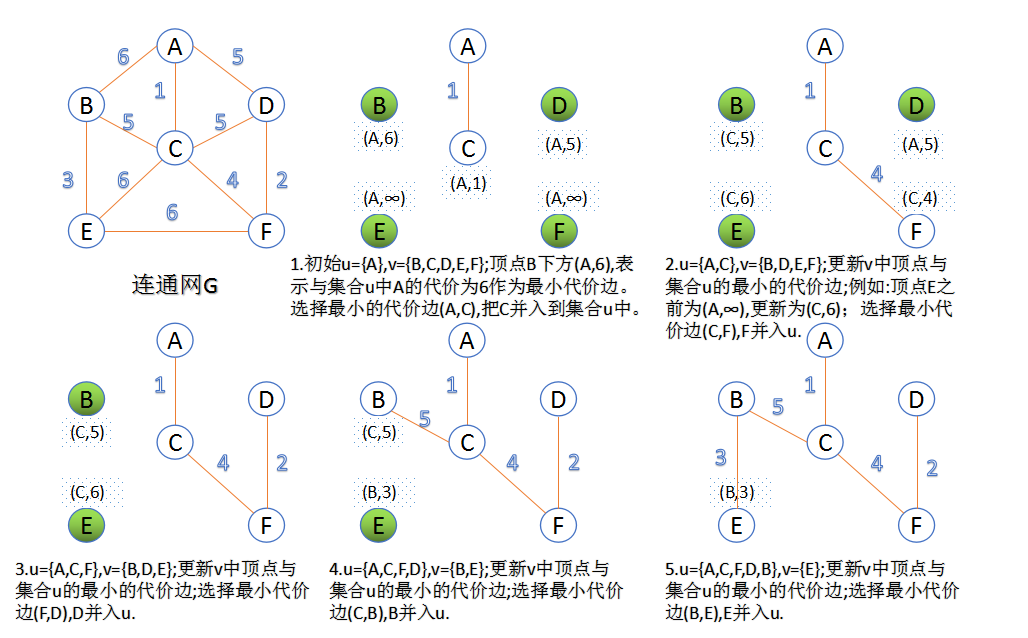
算法导论–最小生成树（Kruskal和Prim算法）

Kruskal

Prim

这个题用Prim居然MLE了….
用并查集维护Kruskal可以过

数据范围1 ≤ N, M ≤ 10000 , 0 ≤ R ≤ 50,000
如果用Prim应该是 20000*20000的邻接表, 用Kruskal则是50000条边, 显然用Kruskal更优~
最小生成树Prim与Kruskal算法的比较

AC代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#define mst(a) memset(a, 0, sizeof a)
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxn = 50000+5;
int f[20000+5];

struct edge{
    int f, t, cost;
}cst[maxn];

bool cmp(const edge& a, const edge& b){
    return a.cost < b.cost;
}

int all, n, m, r;

void bcj_init(){
    for( int i = 0; i < all; i++ )
        f[i] = i;
}

int _find(int a){
    if( a != f[a] ) f[a] = _find(f[a]);
    return f[a];
}

void unite(int a, int b){
    int aa = _find(a);
    int bb = _find(b);
    if( aa != bb ){
        f[bb] = aa;
    }
}

int kruskal(){
    int res = 0;
    bcj_init();
    sort(cst, cst+r, cmp);
    for(int i = 0; i < r; i++){
        edge e = cst[i];
        if( _find(e.f) != _find(e.t) ){
            unite(e.f, e.t);
            res += e.cost;
        }
    }
    return res;
}

int main()
{
    int T, a, b, c;
    scanf("%d",&T);
    while(T--){
        scanf("%d%d%d", &n, &m, &r);
        all = n+m;
        for(int i = 0; i < r; i++){
            scanf("%d%d%d",&a, &b, &c);
            cst[i] = (edge){a, b+n, -c};
        }
        int res = kruskal();
        printf("%d\n",all*10000+res);
    }
    return 0;
}