UVa 10689 - Yet another Number Sequence ( 矩阵快速幂 )

题意

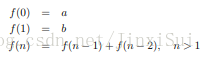
斐波那契数列, 给出a, b ( [0, 100] ), n( [0, 1000000000] ), m ( [1, 4] ) . 求 f(n) 的后m位

思路

因为要求的n非常大, 直接求解是肯定超时的. 这里涉及到利用矩阵快速幂求解递推式 :
由 f(n)=f(n−1)+f(n−2)$f(n)=f(n-1)+f(n-2)$

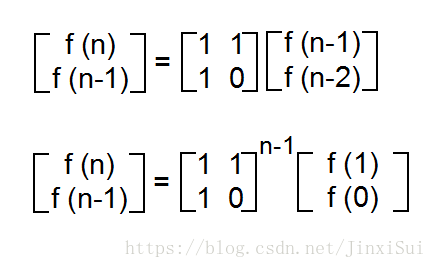
利用矩阵快速幂求出转置矩阵的n-1次幂 再与由f(1) f(0) 构成的矩阵相乘, 得到的矩阵中 mat[0][0] 即为f(n)

AC代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int maxn = 2;
int md[] = {0, 10, 100, 1000, 10000};
int mod;

struct mat
{
    int s[maxn][maxn];
    mat(){
        memset(s,0,sizeof(s));
    };
    mat operator * (const mat& c){
        mat ans;
        for (int i = 0; i < maxn; i++)
            for (int j = 0; j < maxn; j++)
                for (int k = 0; k < maxn; k++)
                    ans.s[i][j] = (ans.s[i][j] + s[i][k] * c.s[k][j])  % mod ;
        return ans;
    }
}str;

mat pow_mod(int k)
{
    if (k == 1)
        return str;
    mat a = pow_mod(k/2);
    mat ans = a * a;
    if (k & 1)
        ans = ans * str;
    return ans;
}

int main()
{
    int T;
    int a, b, n, m;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d%d%d", &a, &b, &n, &m);
        mod = md[m];
        str.s[0][0] = 1;
        str.s[0][1] = 1;
        str.s[1][0] = 1;
        str.s[1][1] = 0;
        mat str2 = pow_mod(n-1);
        printf("%d\n", (b*str2.s[0][0]+a*str2.s[0][1])%mod );
    }
    return 0;
}