SLERP Jacobians (right perturb)

使用右扰动的方式计算 SLERP 的雅克比。是 SLERP Jacobians (left perturb) 的补充。

1. 推导

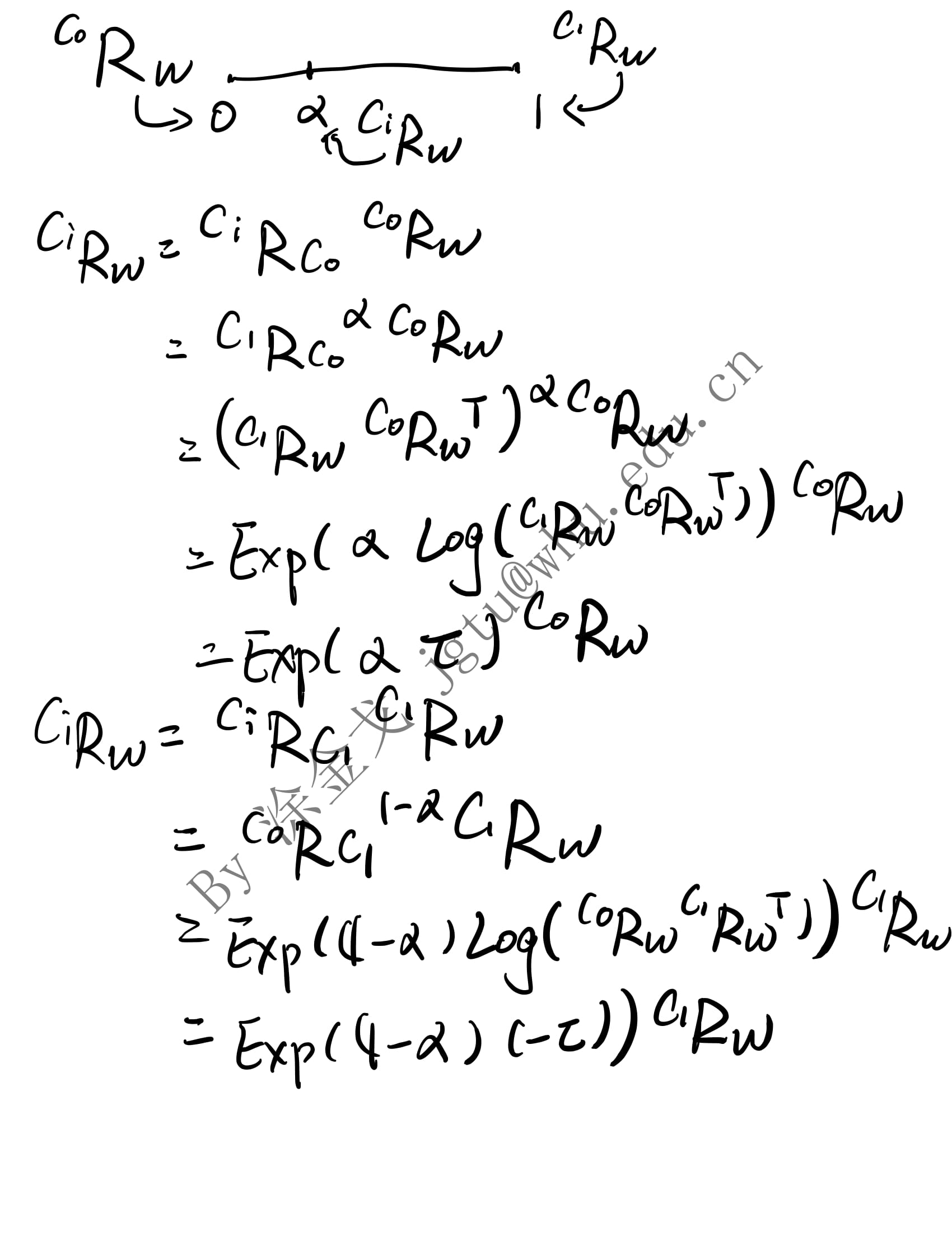
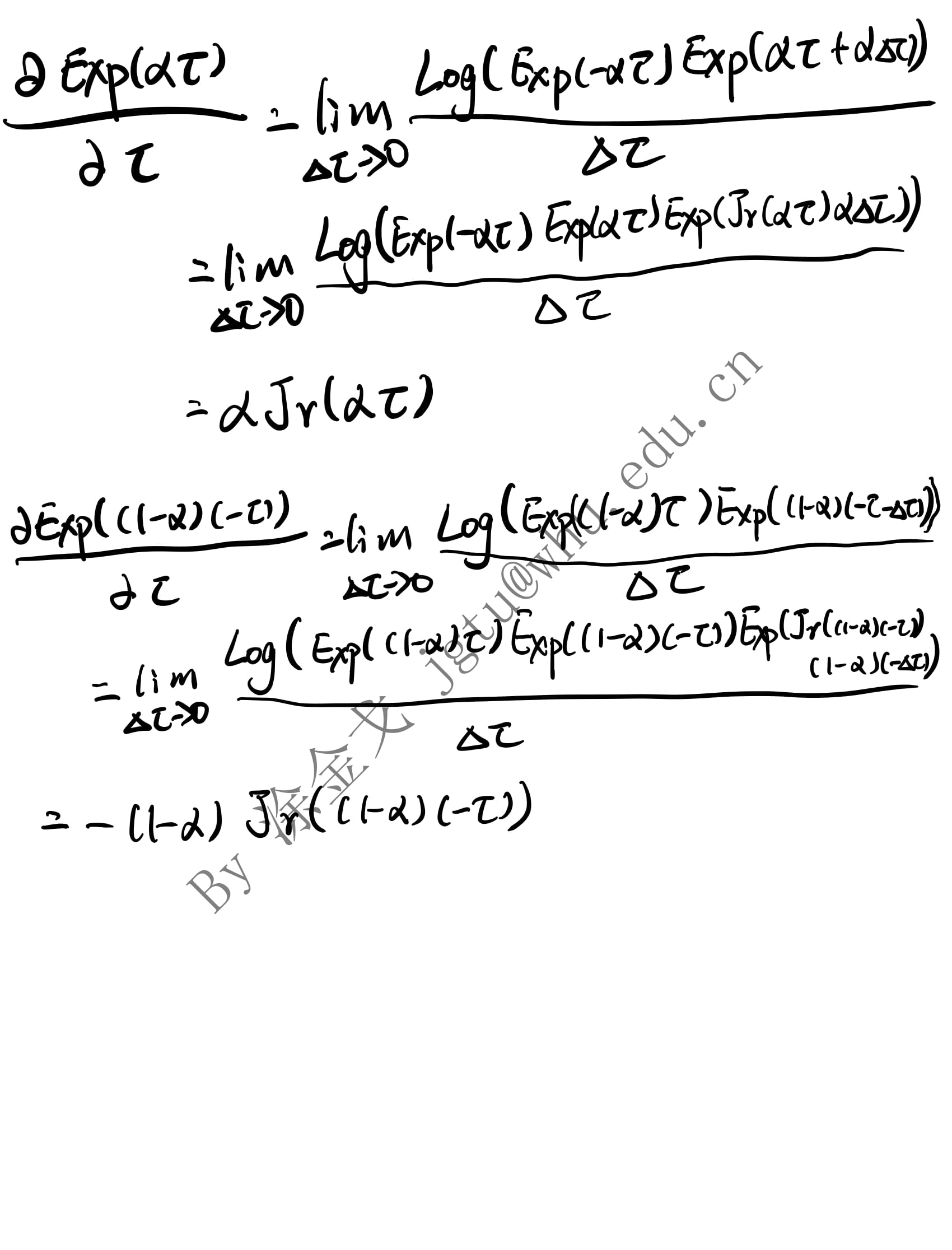
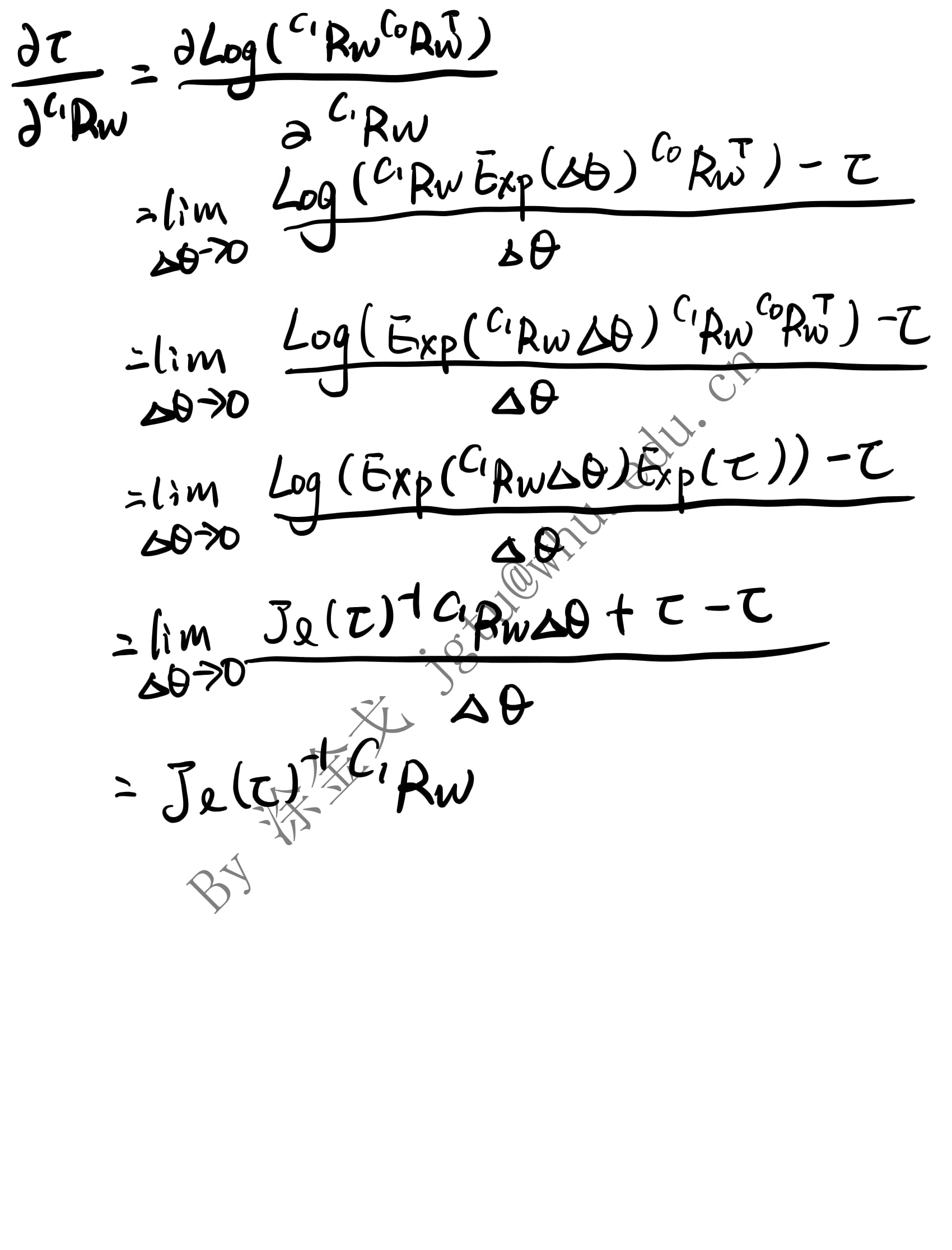
2. 验证

使用 ceres-solver 1.14.0 。

代码如下：

#include <Eigen/Core>
#include <Eigen/Geometry>
#include <ceres/internal/autodiff.h>
#include <ceres/internal/numeric_diff.h>
#include <cstdlib>
#include <ctime>

/// use numeric diff and auto diff to check my analytic diff.

class QuaternionCostFunctor {
public:
  QuaternionCostFunctor(const Eigen::Quaterniond &_ci_q_w) : ci_q_w_{_ci_q_w} {}

  template <typename T>
  bool operator()(const T *const _c0_q_w, const T *const _c1_q_w,
                  const T *const _alpha, T *_e) const {
    const Eigen::Quaternion<T> c0_q_w(_c0_q_w);
    const Eigen::Quaternion<T> c1_q_w(_c1_q_w);

    const Eigen::Quaternion<T> delta_qua = c1_q_w * c0_q_w.inverse();
    Eigen::AngleAxis<T> delta_aa(delta_qua);
    delta_aa.angle() *= _alpha[0];

    const Eigen::Quaternion<T> ci_q_w_p =
        Eigen::Quaternion<T>(delta_aa) * c0_q_w;

    const Eigen::Quaternion<T> ci_q_w(
        static_cast<T>(ci_q_w_.w()), static_cast<T>(ci_q_w_.x()),
        static_cast<T>(ci_q_w_.y()), static_cast<T>(ci_q_w_.z()));

    const Eigen::Quaternion<T> e_q =
        ci_q_w.inverse() * ci_q_w_p; // This direction is important, meeting the
                                     // substraction of right perturbation.

    const Eigen::AngleAxis<T> e_aa(e_q);

    Eigen::Map<Eigen::Matrix<T, 3, 1>> e(_e);

    e = e_aa.axis() * e_aa.angle();

    return true;
  }

  void evaluateAnalytically(const double *const _c0_q_w,
                            const double *const _c1_q_w,
                            const double *const _alpha, double *_e,
                            double **_jacobians) const {
    const Eigen::Quaternion<double> c0_q_w(_c0_q_w);
    const Eigen::Quaternion<double> c1_q_w(_c1_q_w);

    const Eigen::Quaternion<double> delta_qua = c1_q_w * c0_q_w.inverse();
    Eigen::AngleAxis<double> delta_aa(delta_qua);
    delta_aa.angle() *= _alpha[0];

    const Eigen::Quaternion<double> ci_q_w_p =
        Eigen::Quaternion<double>(delta_aa) * c0_q_w;

    const Eigen::Quaternion<double> e_q =
        ci_q_w_.inverse() * ci_q_w_p; // This direction is important, meeting
                                      // the substraction of right perturbation.

    const Eigen::AngleAxis<double> e_aa(e_q);

    Eigen::Map<Eigen::Matrix<double, 3, 1>> e(_e);

    e = e_aa.axis() * e_aa.angle();

    if (_jacobians != nullptr) {
      const Eigen::Vector3d tau_axis = delta_aa.axis();
      const double tau_angle = delta_aa.angle() / _alpha[0];
      if (_jacobians[0] != nullptr) { /// c0_q_w
        Eigen::Map<Eigen::Matrix<double, 3, 4, Eigen::RowMajor>> J(
            _jacobians[0]);
        J.setZero();
        J.block(0, 0, 3, 3) =
            (1 - _alpha[0]) * c1_q_w.inverse().toRotationMatrix() *
            J_r((1 - _alpha[0]) * -tau_angle, tau_axis) *
            J_l_inv(tau_angle, tau_axis) * c1_q_w.toRotationMatrix();
      }
      if (_jacobians[1] != nullptr) { /// c1_q_w
        Eigen::Map<Eigen::Matrix<double, 3, 4, Eigen::RowMajor>> J(
            _jacobians[1]);
        J.setZero();
        J.block(0, 0, 3, 3) = _alpha[0] * c0_q_w.inverse().toRotationMatrix() *
                              J_r(_alpha[0] * tau_angle, tau_axis) *
                              J_l_inv(tau_angle, tau_axis) *
                              c1_q_w.toRotationMatrix();
      }
      if (_jacobians[2] != nullptr) { /// alpha
        Eigen::Map<Eigen::Matrix<double, 3, 1>> J(_jacobians[2]);
        J = c0_q_w.inverse().toRotationMatrix() *
            J_r(_alpha[0] * tau_angle, tau_axis) * tau_angle * tau_axis;
      }
    }
  }

  static bool GlobalToLocal(const double *x, double *jacobian) {
    const double qw = x[3];
    const double qx = x[0];
    const double qy = x[1];
    const double qz = x[2];
    jacobian[0] = qw * 0.5, jacobian[1] = -qz * 0.5, jacobian[2] = qy * 0.5;
    jacobian[3] = qz * 0.5, jacobian[4] = qw * 0.5, jacobian[5] = -qx * 0.5;
    jacobian[6] = -qy * 0.5, jacobian[7] = qx * 0.5, jacobian[8] = qw * 0.5;
    jacobian[9] = -qx * 0.5, jacobian[10] = -qy * 0.5, jacobian[11] = -qz * 0.5;
    return true;
  }

  static inline Eigen::Matrix3d skew(const Eigen::Vector3d &_v) {
    Eigen::Matrix3d res;
    res.setZero();
    res(0, 1) = -_v[2], res(0, 2) = _v[1], res(1, 2) = -_v[0];
    res(1, 0) = _v[2], res(2, 0) = -_v[1], res(2, 1) = _v[0];
    return res;
  }

  static Eigen::Matrix3d J_l(const double _angle,
                             const Eigen::Vector3d &_axis) {
    /// (145)
    Eigen::Matrix3d res =
        Eigen::Matrix3d::Identity() +
        (1 - std::cos(_angle)) / (_angle * _angle) * skew(_angle * _axis) +
        (_angle - std::sin(_angle)) / (_angle * _angle * _angle) *
            skew(_angle * _axis) * skew(_angle * _axis);
    return res;
  }

  static Eigen::Matrix3d J_l_inv(const double _angle,
                                 const Eigen::Vector3d &_axis) {
    /// (146)
    Eigen::Matrix3d res =
        Eigen::Matrix3d::Identity() - 0.5 * skew(_angle * _axis) +
        (1 / (_angle * _angle) -
         (1 + std::cos(_angle)) / (2 * _angle * std::sin(_angle))) *
            skew(_angle * _axis) * skew(_angle * _axis);
    return res;
  }

  static Eigen::Matrix3d J_r(const double _angle,
                             const Eigen::Vector3d &_axis) {
    return J_l(_angle, _axis).transpose();
    /// (143)
    Eigen::Matrix3d res =
        Eigen::Matrix3d::Identity() -
        (1 - std::cos(_angle)) / (_angle * _angle) * skew(_angle * _axis) +
        (_angle - std::sin(_angle)) / (_angle * _angle * _angle) *
            skew(_angle * _axis) * skew(_angle * _axis);
    return res;
  }

  static Eigen::Matrix3d J_r_inv(const double _angle,
                                 const Eigen::Vector3d &_axis) {
    return J_l_inv(_angle, _axis).transpose();
    /// (144)
    Eigen::Matrix3d res =
        Eigen::Matrix3d::Identity() + 0.5 * skew(_angle * _axis) +
        (1 / (_angle * _angle) -
         (1 + std::cos(_angle)) / (2 * _angle * std::sin(_angle))) *
            skew(_angle * _axis) * skew(_angle * _axis);
    return res;
  }

private:
  const Eigen::Quaterniond ci_q_w_;
};

Eigen::Quaterniond getRandomQuaternion() {
  const double range = 1.;

  Eigen::Vector3d axis(std::rand() / double(RAND_MAX) * 2 * range + (-range),
                       std::rand() / double(RAND_MAX) * 2 * range + (-range),
                       std::rand() / double(RAND_MAX) * 2 * range + (-range));
  axis.normalize();
  const double angle = std::rand() / double(RAND_MAX) * 2 * M_PI;
  Eigen::AngleAxisd aa(angle, axis);

  return Eigen::Quaterniond(aa);
}

int main(int argc, char **argv) {

  std::srand(std::time(NULL));

  std::srand(0);

  Eigen::Quaterniond c0_q_w = getRandomQuaternion();
  Eigen::Quaterniond c1_q_w = getRandomQuaternion();
  double alpha = std::rand() / double(RAND_MAX);

  std::cout << "c0_R_w:\n" << c0_q_w.toRotationMatrix() << std::endl;

  std::cout << "c1_R_w:\n" << c1_q_w.toRotationMatrix() << std::endl;

  std::cout << "alpha:\n" << alpha << std::endl;

  const Eigen::Quaterniond delta_qua = c1_q_w * c0_q_w.inverse();
  Eigen::AngleAxisd delta_aa(delta_qua);
  delta_aa.angle() *= alpha;

  const Eigen::Quaterniond ci_q_w = Eigen::Quaterniond(delta_aa) * c0_q_w;

  std::cout << "ci_R_w:\n" << ci_q_w.toRotationMatrix() << std::endl;

  QuaternionCostFunctor functor(ci_q_w);

  double residuals[3];
  double *parameters[3] = {c0_q_w.coeffs().data(), c1_q_w.coeffs().data(),
                           &alpha};
  double **jacobians = new double *[3];
  for (int i = 0; i < 2; ++i)
    jacobians[i] = new double[12];
  jacobians[2] = new double[3];

  {
    ceres::internal::AutoDiff<QuaternionCostFunctor, double, 4, 4,
                              1>::Differentiate(functor, parameters,
                                                3, /// residual num
                                                residuals, jacobians);

    Eigen::Map<Eigen::Matrix<double, 3, 4, Eigen::RowMajor>> jacobian_0(
        jacobians[0]);

    Eigen::Matrix<double, 4, 3, Eigen::RowMajor> global_to_local_0;
    QuaternionCostFunctor::GlobalToLocal(parameters[0],
                                         global_to_local_0.data());

    std::cout << "autodiff jacobian_0:\n"
              << jacobian_0 * global_to_local_0 << std::endl;

    Eigen::Map<Eigen::Matrix<double, 3, 4, Eigen::RowMajor>> jacobian_1(
        jacobians[1]);

    Eigen::Matrix<double, 4, 3, Eigen::RowMajor> global_to_local_1;
    QuaternionCostFunctor::GlobalToLocal(parameters[1],
                                         global_to_local_1.data());

    std::cout << "autodiff jacobian_1:\n"
              << jacobian_1 * global_to_local_1 << std::endl;

    Eigen::Map<Eigen::Matrix<double, 3, 1>> jacobian_2(jacobians[2]);

    std::cout << "autodiff jacobian_2:\n" << jacobian_2 << std::endl;
  }

  {
    ceres::internal::NumericDiff<
        QuaternionCostFunctor, ceres::NumericDiffMethodType::CENTRAL, 3, 4, 4,
        1, 0, 0, 0, 0, 0, 0, 0, 0,
        4>::EvaluateJacobianForParameterBlock(&functor, residuals,
                                              ceres::NumericDiffOptions(),
                                              3, /// residual num
                                              0, /// block index
                                              4, /// block size
                                              parameters, jacobians[0]);

    Eigen::Map<Eigen::Matrix<double, 3, 4, Eigen::RowMajor>> jacobian_0(
        jacobians[0]);

    Eigen::Matrix<double, 4, 3, Eigen::RowMajor> global_to_local_0;
    QuaternionCostFunctor::GlobalToLocal(parameters[0],
                                         global_to_local_0.data());

    std::cout << "numdiff jacobian_0:\n"
              << jacobian_0 * global_to_local_0 << std::endl;
  }

  {
    ceres::internal::NumericDiff<
        QuaternionCostFunctor, ceres::NumericDiffMethodType::CENTRAL, 3, 4, 4,
        1, 0, 0, 0, 0, 0, 0, 0, 1,
        4>::EvaluateJacobianForParameterBlock(&functor, residuals,
                                              ceres::NumericDiffOptions(),
                                              3, /// residual num
                                              1, /// block index
                                              4, /// block size
                                              parameters, jacobians[1]);

    Eigen::Map<Eigen::Matrix<double, 3, 4, Eigen::RowMajor>> jacobian_1(
        jacobians[1]);

    Eigen::Matrix<double, 4, 3, Eigen::RowMajor> global_to_local_1;
    QuaternionCostFunctor::GlobalToLocal(parameters[1],
                                         global_to_local_1.data());

    std::cout << "numdiff jacobian_1:\n"
              << jacobian_1 * global_to_local_1 << std::endl;
  }

  {
    ceres::internal::NumericDiff<
        QuaternionCostFunctor, ceres::NumericDiffMethodType::CENTRAL, 3, 4, 4,
        1, 0, 0, 0, 0, 0, 0, 0, 2,
        1>::EvaluateJacobianForParameterBlock(&functor, residuals,
                                              ceres::NumericDiffOptions(),
                                              3, /// residual num
                                              2, /// block index
                                              1, /// block size
                                              parameters, jacobians[2]);

    Eigen::Map<Eigen::Matrix<double, 3, 1>> jacobian_2(jacobians[2]);

    std::cout << "numdiff jacobian_2:\n" << jacobian_2 << std::endl;
  }

  {
    functor.evaluateAnalytically(parameters[0], parameters[1], parameters[2],
                                 residuals, jacobians);

    Eigen::Map<Eigen::Matrix<double, 3, 4, Eigen::RowMajor>> jacobian_0(
        jacobians[0]);
    Eigen::Map<Eigen::Matrix<double, 3, 4, Eigen::RowMajor>> jacobian_1(
        jacobians[1]);
    Eigen::Map<Eigen::Matrix<double, 3, 1>> jacobian_2(jacobians[2]);

    std::cout << "analytic jacobian_0:\n"
              << jacobian_0.block(0, 0, 3, 3) << std::endl;
    std::cout << "analytic jacobian_1:\n"
              << jacobian_1.block(0, 0, 3, 3) << std::endl;
    std::cout << "analytic jacobian_2:\n" << jacobian_2 << std::endl;
  }

  return 0;
}

3. 用 Conan 解决依赖

conanfile.txt:

[requires]
ceres-solver/1.14.0

[generators]
cmake

CMakeLists.txt:

cmake_minimum_required(VERSION 3.5)

project(helloworld)

include(${CMAKE_BINARY_DIR}/conanbuildinfo.cmake)
conan_basic_setup()

include_directories(${EIGEN3_INCLUDE_DIR})

add_executable(left left.cc)
target_link_libraries(left ${CONAN_LIBS})

add_executable(right right.cc)
target_link_libraries(right ${CONAN_LIBS})