1254.统计封闭岛屿的数目

有一个二维矩阵 grid ，每个位置要么是陆地（记号为 0 ）要么是水域（记号为 1 ）。

我们从一块陆地出发，每次可以往上下左右 4 个方向相邻区域走，能走到的所有陆地区域，我们将其称为一座「岛屿」。

如果一座岛屿 完全 由水域包围，即陆地边缘上下左右所有相邻区域都是水域，那么我们将其称为 「封闭岛屿」。

请返回封闭岛屿的数目。

示例 1：

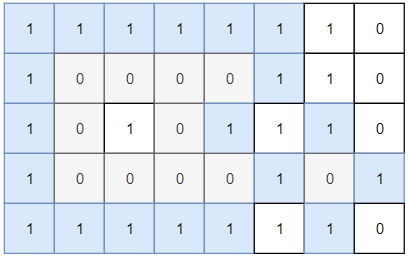
输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出：2
解释：
灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。

示例 2：

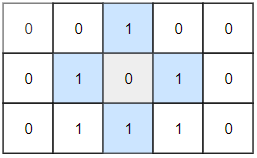
输入：grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
输出：1

示例 3：

输入：grid = [[1,1,1,1,1,1,1],
             [1,0,0,0,0,0,1],
             [1,0,1,1,1,0,1],
             [1,0,1,0,1,0,1],
             [1,0,1,1,1,0,1],
             [1,0,0,0,0,0,1],
             [1,1,1,1,1,1,1]]
输出：2

提示：

• 1 <= grid.length, grid[0].length <= 100
• 0 <= grid[i][j] <=1

为了练习DFS才写的这道题目，这个题目不难，但是如果之前没见过的话可能会很难想出来。

思路很简单，第一步：找到边界上的所有的0，把它及周围的0全部变成1

第二部，找到里面的0，每找到一个，把岛屿数目加1，把它及周围的0变成1

class Solution {
	    public int closedIsland(int[][] grid) {
            //找到边界上的0，把它变成1
	    	for(int i = 0; i < grid.length; i++) {
	    		for(int j = 0; j < grid[0].length; j++) {
	    			if(i == 0 || i == grid.length-1 || j == 0 || j == grid[0].length -1) {
	    				if(grid[i][j] == 0)
	    				change(i, j, grid);
	    			}
	    		}
	    	}
	    	int res = 0;
            //找到里面的0，把它变成1，岛屿数量加1
	    	for(int i = 0; i < grid.length; i++) {
	    		for(int j = 0; j < grid[0].length; j++) {
	    			if(grid[i][j] == 0) {
	    				change(i, j, grid);
	    				res++;
	    			}
	    		}
	    	}
	    	return res;
	    }
	    
    	//把0变成1的函数
	    public void change(int x,int y,int[][] grid) {
	    	grid[x][y] = 1;
            //用来走上下左右四个方向的数组，如果是8个方向可以用长度为8的两个数组，也可以用两重循环
	    	int[] cx = new int[] {-1,0,1,0};
	    	int[] cy = new int[] {0,1,0,-1};
			for(int i = 0; i <= 3; i++) {
					int nx =x + cx[i];
					int ny =y + cy[i];
                	//走到的0在矩阵内，把它变成1，对它也进行上下左右四个方向的搜索
					if(nx >=0 && nx < grid.length && ny >=0 && ny < grid[0].length && 
						grid[nx][ny] == 0) {
						change(nx, ny, grid);
					}
			}
		}
	}