洛谷P1044 栈

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

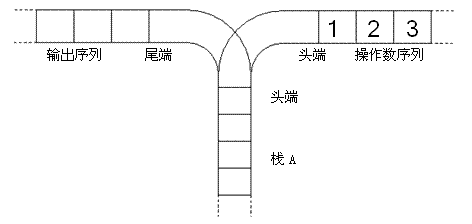
宁宁考虑的是这样一个问题：一个操作数序列，1,2,\ldots ,n1,2,…,n（图示为 1 到 3 的情况），栈 A 的深度大于 nn。

现在可以进行两种操作，

  1. 将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
  2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。

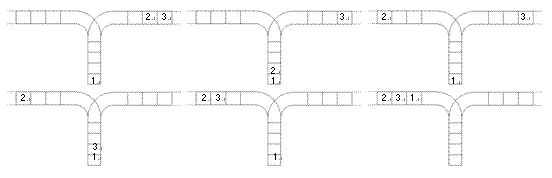
（原始状态如上图所示）

你的程序将对给定的 nn，计算并输出由操作数序列 1,2,\ldots,n1,2,…,n 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 nn（1 \leq n \leq 181≤n≤18）。

输出格式

输出文件只有一行，即可能输出序列的总数目。

输入输出样例

输入 #1

3

输出 #1

5

解题思路一：卡特兰数
Cantalan数 推导式为：h[n]=((4n-2)/(n+1))h[n-1]
这应该能算是一个定理了吧
这个式子所描述的关系是：
一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?
也就是上面的那道题
如果你已经知道了这个定理，那么可以直接递推
代码如下

#include<bits/stdc++.h>
using namespace std;
unsigned long int n;
int h[31]; 
int main()
{
    cin>>n;
    h[0]=h[1]=1;
    h[2]=2;
    h[3]=5;
    for(int i=4;i<=n;i++)
    {
        for(int j=0;j<i;j++)
        {
            h[i]+=h[j]*h[i-j-1]; 
        }
    }
    cout<<h[n]; 
    return 0;
}

       解题思路二：推出卡特兰公式

       没啥说的，我先吐为敬

       首先，我们设f（n）=序列个数为n的出栈序列种数。（我们假定，最后出栈的元素为k，显然，k取不同值时的情况是相互独立的，也就是求出每种k最后出栈的情况数后可用加法原则，由于

k最后出栈，因此，在k入栈之前，比k小的值均出栈，此处情况有f(k-1)种，而之后比k大的值入栈，且都在k之前出栈，因此有f(n-k)种方式，由于比k小和比k大的值入栈出栈情况是相互独立的，此处可用乘法原则，f(n-k)*f(k-1)种，求和便是Catalan递归式

       首次出空之前第一个出栈的序数k将1~n的序列分成两个序列，其中一个是1~k-1，序列个数为k-1，另外一个是k+1~n，序列个数是n-k。

       此时，我们若把k视为确定一个序数，那么根据乘法原理，f（n）的问题就等价于——序列个数为k-1的出栈序列种数乘以序列个数为n - k的出栈序列种数，即选择k这个序数的f（n）=f（k-1）×f（n-k）。而k可以选1到n，所以再根据加法原理，将k取不同值的序列种数相加，得到的总序列种数为：f（n）=f（0）f（n-1）+f（1）f（n-2）+……+f（n-1）f（0）。

看到此处，再看看卡特兰数的递推式，答案不言而喻，即为f（n）=h（n）= C（2n,n）/（n+1）= c（2n,n）-c（2n,n-1）（n=0，1，2，……）。

        最后，令f（0）=1，f（1）=1。

        很显然这不大现实...我也是知道这个式子反推的...

        难道不知道这个式子就做不出来这题了吗？

        众所周知OI是一门玄学

        所以我们当然要枚举前四项，这不是很正常的事吗（bushi

        当1在第1个时：前面有一种状况：？（是不是感觉和n=0很像）；后面有两种状况：2 3和3 2（是不是感觉和n=2很像）

        当1在第2个时：前面有一种状况：2（是不是感觉和n=1很像）；后面有一种状况：3（是不是感觉和n=1很像）

        当1在第3个时，前面有两种状况：2 3和3 2（是不是感觉和n=2很像），后面有一种状况：？（是不是感觉和n=0很像）

         当1在第i个时，前面就是2~i的一个出栈序列，后面就是i+1~n的一个序列。

        于是我们设这n个数的出栈序列为f[n]，则根据乘法原理有：

        f(n)= f(0)f(n-1)+f(1)f(n-2) + ... +f(n-1)*f(0) (n>=2)

        这**不就是卡特兰么！

        于是就...做完了

 

                  其实这个题算是来补充知识的，卡特兰数在后面涉及到栈的OI题里面肯定会提到，所以把这个题插在这里天衣无缝（bushi
                  表明了这货完全是个数学题
                  数学学好了，代码不重要（bushi
                  如果DFS应该也能做，但是我不大熟练啊...

posted @ 2020-05-03 20:05  JiangXingchen  阅读(427)  评论(0)  编辑  收藏  举报
Live2D