好题题集2

毒瘤思维题汇总1

毒瘤思维题汇总2

好题题集1

Combining Slimes

有 \(n\) 个位置，每次会以 \(p\) 的概率在最右边加入一个数 \(1\) ，\(1-p\) 的概率在最右边加入一个数 \(2\)。任意时刻如果发现存在两个相邻的数 \(x\)，立即合并为 \(x+1\)。问将 \(n\) 个位置填满时所有位置上的数的和的期望值。

\(1 \le n \le 10^9,0 < p < 1\)，精度要求 \(10^{-4}\)

发现出现超过 \(50\) 的数的概率是非常小的，于是我们只需要考虑每个数的值不超过 \(50\) 的情况。

设 \(a(i,j)\) 表示用 \(i\) 个位置，可以造出 \(j\)（即最后最左边的数 \(\ge j\)）的概率，那么有 \(a(i,j) = a(i,j-1) \cdot a(i-1,j-1)\)。不难发现，\(a(i,j) = a(j,j),i \ge j\)。那么 \(a\) 也是 \(50 \times 50\) 的级别。

现在我们可以考虑DP求解了。共 \(i\) 个位置，最终第一个恰好为 \(j\) 的概率为 \(a(i,j) \cdot (1-a(i-1,j))\)，设其为 \(a'(i,j)\)。设 \(f(i,j)\) 表示 \(i\) 个位置，如果第一个位置为 \(j\)，那么总和的期望是多少。

对于 \(j = 1\)，根据条件概率公式，有：

\[f(i,1) = 1 + \frac{\sum_{k > 1} f(i-1,k) \cdot b'(i-1,k)}{\sum_{k > 1} b'(i-1,k)} \]

其中 \(b'\) 是一个与 \(a'\) 类似的数组，只不过还要求第一个数为 \(2\)。

对于 \(j > 1\)，同样有：

\[f(i,j) = j + \frac{\sum_{k < j}f(i-1,k) \cdot b'(i-1,k)}{\sum_{k < j} b'(i-1,k)} \]

矩阵加速即可。

复杂度：\(O(50^3 \log n)\)

染色

有 \(2 \times n\) 的网格图，\(C\) 种颜色，已经有一些网格染上了颜色。

求有多少种染色方案，使得不存在两个相邻的网格颜色相同。

\(1 \le n \le 10^5,5 \le C \le 10^5\)

相当不错的码农题。

如果所有网格均尚未染色，那么方案数为 \(C \cdot (C-1) \cdot ((C - 2) \cdot (C - 2) + (C - 1))^{n-1}\)（给第一列钦定两个颜色，然后后面的递推是类似的）。我们可以用这种思想干掉两边的空网格。

考虑一个暴力的DP：设 \(f(i,j,k)\) 表示考虑了前 \(i\) 列，第 \(i\) 列的颜色为 \(j\) 和 \(k\) 的方案数。转移就是枚举当前列的两种颜色，判断合不合法。复杂度：\(O(nC^4)\)。就算用上前缀和优化，也不过 \(O(nC^2)\)，毕竟光状态数就有这么多。

考虑优化状态。如果每一列都至少有一个格子有颜色就好了。注意到那些两个格子都为空的列，虽然其状态数很多，但是这种列的样子只有一种，于是或许可以预处理掉。预处理出 \(g(i,tp)\) 表示在相距 \(i\) 的两列（且这两列的关系为 \(tp\) ）之间填满空列的方案数。手动枚举一下，关系大致有五种：

0 : 
a a
b b

1 : 
a b
b a

2 : 
a a | a c
b c | b b

3 :
a c | a b
b a | b c

4 :
a c
b d

其中第 \(2,3\) 中虽然有两种形态，但是看起来类似，就归到一起了。

\(g(i,tp)\) 可以DP出来，大致是从 \(g(i-1,s)\) 转移到 \(g(i,t)\)。复杂度为 \(O(n)\)，不是瓶颈。

有了 \(g\) 以后，我们就只用在至少一个格子有颜色的列上DP了，状态可以设为 \(f(i,c)\) 表示前 \(i\) 列，第 \(i\) 列的尚未决定的格子（都染过色，则特判）的颜色为 \(c\) 的方案数。转移就枚举当前列的颜色，结合前缀和优化大力讨论一下就好了。复杂度为 \(O(n^2)\)（\(n,C\) 同阶）。

发现那个优化其实不是前缀和优化，我们只需要做的是全局加，全局乘，全局赋值，单点赋值，全局求和，单点查询。这个可以用 快速查询 的暴力做，复杂度为 \(O(n \log n)\)。

代码实现有一定的难度。

最长上升子序列

easy version：给定一个序列 $ B_m = (b_1, b_2, \cdots, b_m) $，设 $ C $ 是 $ B_m $ 的子序列，且 $ C $ 的最长上升子序列的长度不超过 $ k $，则 $ C $ 的长度最大能是多少？

hard version：给你这样一个序列 $ B = (b_1, b_2, \ldots, b_n) $，以及若干次询问。每次询问会给定两个整数 $ m $ 和 $ k $，你需要对于 $ B $ 序列的前 $ m $ 个元素构成的序列 $ B_m = (b_1, b_2, \cdots, b_m) $ 和 $ k $ 回答上述问题。

求解 hard version

\(1 \le n,b \le 5 \cdot 10^4,1 \le q \le 2 \cdot 10^5\)

涉及到了杨表的相关内容。杨表是一个类似锯齿状的网格图，由若干左对齐的行组成，每行的列数逐渐递减。满足 \((i,j) < (i+1,j),(i,j) < (i,j+1)\)。当然，也可以换成 \(>,\le, \ge\)，也叫杨表。

有一个和这个题关系不大的结论：将长为 \(n\) 的排列填入某一给定杨表（给定行数和每行的列数）的方案数为 \(\frac{n!}{\prod_{(i,j)}c(i,j)}\)，其中 \(c(i,j)\) 为 \((i,j)\) 的正右边的格子数加正下方的格子数加1.可以用除法原理（大概是吧）理解。

构造：增量法，有一个单个增量 \(O(r\log c)\) 的构造杨表的方法：从第一行开始，如果这一行全比这个数小，就把这个数扔到这一行的末尾，结束；否则，找到这个数的后继（第一个小于或大于或小于等于或大于等于这个数的数），把这个数扔到后继的位置，把这个后继扔到下一行递归去做。不难发现这种方法对数的插入顺序无关。

杨表还有个性质：如果把判断符号取反（例如 \(<\) 变成 \(\ge\)），那么杨表的形状会转置。

回到这个题。首先根据 Dilworth 定理可以将最长上升子序列转化成选最少的不下降子序列覆盖整个序列，于是题意变成对于某个前缀，取出 \(k\) 个不下降子序列，使得取出的数尽可能多。这对应着判断符号为 \(\ge\) 杨表的前 \(k\) 行（类似二分DP数组求LIS的方法）。于是我们可以将询问离线排序，问题转化为动态加数，查杨表前 \(k\) 行的数的个数和。复杂度可以做到 \(O(nr\log c)\)。

然而复杂度还是有点高，但是发现每个格子所在的行的编号和列的编号一定至少有一个小于 \(\sqrt n\)。于是同时维护两种杨表，每次插入到第 \(\sqrt n\) 行就强制结束即可。复杂度 \(O(n\sqrt n \log n)\)。

Planar Graph

给一张 \(n\) 个点 \(m\) 条边的简单无向平面图，保证无割点割边。给定每个点的坐标。

\(q\) 组询问，每次给出 \(x_1,x_2,...,x_k\)，保证边 \((x_i,x_{i+1})\) 存在，求由这 \(k\) 个点组成的环的环内+环上的点的个数。保证这是个简单环。

\(1 \le n,m,q,\sum k \le 10^5\)

和 矿区 几乎完全一致，只不过那题求的是环内的区域数，所以需要转对偶图；这题求的是点数，于是不用转对偶图了，直接跑个生成树即可。

具体做法：跑一个生成树（内向），保证根在每个环的外部，边权为子树点数，反向边的边权为正向边边权的相反数。那么答案即为流出环的边权和 减去 流入环的边权和。

发现对于环上的每个点，与其相连的在环外的边是按照极角序排序后的连续的区间。于是提前 sort 一下即可。

复杂度：\(O(n \log n)\)

蔬菜

小 N 是蔬菜仓库的管理员，负责设计蔬菜的销售方案。
在蔬菜仓库中，共存放有 \(n\) 种蔬菜，小 N 需要根据不同蔬菜的特性，综合考虑各方面因素，设计合理的销售方案，以获得最多的收益。
在计算销售蔬菜的收益时，每销售一个单位第 \(i\) 种蔬菜，就可以获得 \(a_i\) 的收益。
特别地，由于政策鼓励商家进行多样化销售，第一次销售第 \(i\) 种蔬菜时，还会额外得到 \(s_i\) 的额外收益。
在经营开始时，第 \(i\) 种蔬菜的库存为 \(c_i\) 个单位。
然而，蔬菜的保鲜时间非常有限，一旦变质就不能进行销售，不过聪明的小 N 已 经计算出了每个单位蔬菜变质的时间：对于第 \(i\) 种蔬菜，存在保鲜值 \(x_i\)，每天结束时会 有 \(x_i\) 个单位的蔬菜变质，直到所有蔬菜都变质。（注意：每一单位蔬菜的变质时间是固 定的，不随销售发生变化）
形式化地：对于所有的满足条件 \(d\times x_i \leq c_i\) 的正整数 \(d\) ，有 \(x_i\) 个单位的蔬菜将在 第 \(d\) 天结束时变质。
特别地，若 \((d−1)\times x_i \leq c_i < d\times x_i\) ，则有 \(c_i−(d−1)\times x_i\) 单位的蔬菜将在第 \(d\) 天结束时变质。
注意，当 \(x_i = 0\) 时，意味着这种蔬菜不会变质。
同时，每天销售的蔬菜 . 总量也是有限的，最多不能超过 \(m\) 个单位。
现在，小 N 有 \(k\) 个问题，想请你帮忙算一算。每个问题的形式都是：对于已知的 \(p_j\)，如果需要销售 \(p_j\) 天，最多能获得多少收益？

\(1 \le n,k \le 10^5,1 \le m \le 10\)

神仙贪心题。其弱化版为Supermarket。

将每种蔬菜拆成 \(c_i\) 份，这样每份就有了一个固定的过期时间，并且要让一份的价格加上 \(s_i\)。和弱化版一样，我们将各蔬菜按价值排序，依次放到其快过期的那一天。如果那一天已经满了，就在往前放，这一过程可以用并查集加速。

但是查出来的份数的总和可能有 \(10^{14}\) 这么多，可以对于每种蔬菜合并考虑，用大根堆维护。

还有各 \(p_j\) 的限制，不难发现我们一定会选择（不考虑 \(p_j\) 限制时求出的）前 \(p_j \cdot m\) 个成功操作，并且这是可以实现的。

复杂度：\(O(nm \log n)\)。

生成树求和 加强版

给定一张 \(n\) 个点 \(m\) 条边的无向连通图。定义一棵生成树的权值为其所有边进行三进制不进位加法的权值。

求这张无向连通图的所有生成树的权值和（十进制进位加法）。

\(1 \le n \le 100, m \le \frac{n \cdot (n-1)}{2}, a_i \le 10000\)

又学死了/kk

显然要拆位。一眼类似 Stranger Trees 那道题，于是想把树的权值表示成多项式形式；又想要区分出来 \(1\) 和 \(2\)，于是想到用哈希解决，分别设为 \(x\) 和 \(x^n\)。再配合高斯消元插值，可以做到 \(O(n^5 \log a)\) 的复杂度，又慢又难写。

实际上我们不必得知 \(0,1,2\) 分别有多少个，我们只需要知道 \(0,1,2\) 权值和模 \(3\) 的值即可。于是直接设 \(1,x,x^2\)，就能做到 \(O(n^4 \log a)\)。这已经优秀很多了。

然而我们需要做到 \(n^3 \log a\)。可以全程用多项式进行运算，对 \(x^3\) 取模。应该也是可以的吧，但是求逆那块会非常麻烦。

考虑 DFT 的过程。我们代入 \(w_3^0,w_3^1,w_3^2\)，以实现对 \(3\) 的循环卷积。最后在 IDFT 一下即可。

注意到 \(w_3^0 + w_3^1 + w_3^2 = 0\)，于是我们只需要用 \((a,b)\) 来表示一个数。可以定义其加减乘除。

复杂度：\(O(n^3 \log a)\)

Piet's Palette

有 \(n\) 个位置，每个位置 \(i\) 一开始有个颜色 \(c_i\)（红，黄，蓝，白），但是不告诉你。

规定 \(k\) 个颜色的“染色结果” \(f(c_{1},...,c_{k})\) 的计算方法为：

拿出前两个颜色 \(c_{1},c_{2}\)，如果有一个是白的，那么答案为另一种颜色拼上剩下的颜色序列，递归求解；如果都不是白的，且相同，那么答案为剩下的颜色序列的答案；如果都不是白的且不同，那么答案为红黄蓝中剩下的那种颜色拼上剩下的颜色序列的答案。

特别的，如果 \(k=0\)，那么答案为白色；如果 \(k=1\)，那么答案为 \(c_1\)。

现在有 \(q\) 次操作，共四种：

mix ：给定一些位置，告诉你这些位置的颜色按顺序的染色结果是什么。（这些位置的颜色不改变）

RY ：给定一些位置，如果某个位置颜色为 R，那么变为 Y；如果为 Y 变为 R；否则不变。

RB ：给定一些位置，如果某个位置颜色为 R，那么变为 B；如果为 B 变为 R；否则不变。

YB ：给定一些位置，如果某个位置颜色为 Y，那么变为 B；如果为 B 变为 Y；否则不变。

求任意一种合法的初始颜色序列，或判定无解。

\(1 \le n,q \le 1000\)

好妙的一道题！

如果我们把颜色编号，W = 0,R = 1,B = 2, Y = 3，那么发现 mix 其实就是求了个异或和；RY 为二进制低位异或上高位；RB 为二进制两位交换；YB 为二进制高位异或上低位。

列方程。对于每个 mix 我们可以得到一个方程。这样就有 \(2n\) 个变量和最多 \(2q\) 个方程。bitset 优化高斯消元求可行解即可。

复杂度：\(O(n^3 / w)\)

Beads

有 \(m\) 种不同颜色的珠子，颜色分别为 \(1...m\)，每一种颜色的珠子有任意多个。你需要从中选出 \(n\) 个珠子构成一个项链。

如果经过任意次以下的操作后项链 A 变为了 B，我们就认为 A 与 B 等价。

（1）将项链旋转。
（2）将项链翻转。
（3）同时将项链上的每一颗珠子替换成它的下一种颜色，颜色 \(i\) 将被替换为 \(i \mod m + 1\)。

求最后不同的项链的个数。

\(3 \le n,m \le 10^{18}\)

首先考虑这题的弱化版：只有旋转同构和翻转同构。这是一道经典的 Polya 定理题。

一共有 \(2n\) 种置换：\(n\) 种旋转，\(n\) 种翻转。只需对旋转和翻转分别求出不动点个数总和即可。

旋转：枚举转了 \(d\) 下，那么会有 \(g = (d, n)\) 个循环置换（环），每个环的大小均为 \(\frac{n}g\)，我们要求每个环的颜色必须相同，那么共有 \(m^{g}\) 种方案，总不动点数为 \(\sum_d m^{(n,g)}\)。

翻转：分 \(n\) 的奇偶性考虑：\(n\) 为奇数，则对称轴上有一个点，其余的环有两个点，总共 \(\frac{n+1}{2}\) 个环，贡献为 \(nm^{(n+1)/2}\)；\(n\) 为偶数，有两种对称轴：一种有两个点在对称轴上，有 \(n/2 + 1\) 个环，贡献为 \(n/2 \cdot m^{n/2 + 1}\)；另一种对称轴上没有点，有 \(n/2\) 个环，贡献为 \(n/2 \cdot m^{n/2}\)。

加一块除个 \(2n\) 即可。

现在考虑颜色变换。一共有 \(2nm\) 种置换，照样分旋转和翻转考虑：

旋转：枚举转了 \(d\) 下，那么会有 \(g=(d,n)\) 个环，每个环大小为 \(n/g\)。如果颜色变化为 \(+c\)，那么我们要求环上第二个颜色等于原来第一个颜色；第三个颜色等于原来第二个颜色...第一个颜色等于原来第 \(n\) 个的颜色，这样才算不动点。这相当于要求 \(\frac{n}{g} \cdot c \equiv 0 \pmod m\)，即 \(\dfrac{m}{(m,\frac{n}{g})} | c\)，这样的 \(c\) 有 \((m,\frac{n}g)\) 种。即总贡献为：

\[\sum_dm^g (m,\frac{n}{g}) \]

化简后可以 \(O(\sigma(n))\) 求出。但是需要用 Pollard Rho 加速筛约数。

翻转：

\(n\) 为奇数：颜色变换只能 \(+0\)，因为存在大小为 \(1\) 的环。

\(n\) 为偶数：对称轴上两个点：颜色变化只能 \(+0\)，因为存在大小为 \(1\) 的环；对称轴上没有点：所有环大小为 \(2\)，于是颜色变化有 \((m,2)\) 种方案。

最后加一块即可。

Eternal Average

黑板上有\(n\)个 1 和 \(m\) 个 0，我们每次选择 \(k\) 个数字将其擦除，然后把它们的平均数写上去，这样一直操作直到只剩下一个数，问剩下的这个数字有多少种不同的情况。

\(2 \le n,m,k \le 2000\)

好妙的题！

题意可以用一个满 \(k\) 叉树来表示，共有 \(n\) 个 \(1\) 叶子和 \(m\) 个 \(0\) 叶子。不难发现第 \(i\) 层的叶子的贡献为 \(k^{-i}\) 倍。那么我们就可以用若干形如 \(k^{-i}\) 的 \(0,1\) 来表示了。显然，如果把 \(0\) 也看作 \(1\)，那么所有的这样的 \(k^{-i}\) 的和为 \(1\)。

我们把树抽象成 \(k\) 进制小数，\(1\) 的为 \(z\)，\(0\) 的为 \(1-z\)。在不进位的时候，\(z\) 的数位和为 \(n\)，\(1-z\) 的数位和为 \(m\)；那么在进位的时候，\(z\) 的数位和不超过 \(n\)，并且应该是减去了若干个 \(k-1\)；同时，当我们得到了一个（进位后）\(z\) 的数位和为 \(n-\) 若干个 \(k-1\) 的 \(z\) 的时候，我们也不难构造出至少一个合法的不进位的 \(z\)。

考虑 \(1-z\) 的限制。列竖式得，在小数位中，最后一位为 \(k - z_i\)，其余位为 \(k-1-z_i\)。那么这里的限制为 \(1 + \sum k-1-z_i \le m\) 和 \(1+\sum k-1-z_i \equiv m \pmod {k-1}\)。

注意到小数位不会很长，最多 \(n+m\) 位，于是我们可以直接DP。设 \(f(i,j,0/1)\) 表示（进位后） \(z\) 的小数位中前 \(i\) 位的和为 \(j\)，且最后是不是 \(0\)，的方案数。转移就考虑最后一位是什么直接转移，前缀和优化后可以 \(O(n^2)\) 地求出 \(f\)。最后选择合法的 \((i,j)\) 计入答案。

谢特

对于一长为 \(n\) 的字符串，后缀 \(S_i = S(i...n)\) 有权值 \(w_i\)。

对于 \(i \not= j\)，有 \(val_{i,j} = LCP(S_i, S_j) + (w_i \oplus w_j)\)，其中 \(\oplus\) 为异或。

求最大的 \(val_{i,j}\)。

\(1 \le n,w_i \le 10^5\)

\(LCP\) 可以通过后缀数组的 \(height\) 数组转化为区间的最小值。那么问题可以转化为：有两个数组 \(h_i\) 和 \(w_i\)，对于 \(i \le j\)，有 \(val_{i,j} = (w_{i-1} \oplus w_j) + \min_{i \le k \le j} h_k\)，求最大的 \(val_{i,j}\)。

然后对于 \(val_{i,j} = ...+\min_{i \le k \le j} h_k\)，有一个比较套路的做法（好像叫启发式分治？）：找到 \(h_k\) 最小的那个 \(k\) ，那么跨越 \(k\) 的区间的最小值都是 \(h_k\)，我们只需计算 \(w_{i-1} \oplus w_j\) 的最大值，并递归子问题即可。求 \(w_{i-1} \oplus w_j\) 可以通过可持久化 Trie 的方法以 \(O(\min(len_l,len_r))\) 的时间复杂度解决。于是总复杂度为 \(O(n \log n)\)

蒜头的奖杯

给定长度为 $ n $ 的六个序列 $ A,B,C,D,E,F $ ，求：

\[\sum_{i = 1}^n \sum_{j = 1}^n \sum_{k = 1}^n A_i B_j C_k D_{\gcd(i,j)} E_{\gcd(i,k)} F_{\gcd(j,k)} \]

\(1 \le n \le 10^5\)，所有数不超过 \(10^{18}\)

先考虑这题的弱化版：求

\[\sum_{i=1}^n \sum_{j=1}^n A_iB_jC_{(i,j)} \]

这个比较简单，一种可行的做法是：

\[\begin{aligned} \sum_g C_g \sum_{i=1}^{n/g} \sum_{j=1}^{n/g} A_{ig} B_{jg}\\ = \sum_g C_g \sum_{d=1}^{n/g} \mu(d) (\sum_{i=1}^{n/dg}A_{idg}) (\sum_{i=1}^{n/dg} B_{idg})\\ = \sum_g C_g \sum_{d=1}^{n/g } \mu(d) F_A(dg) F_B(dg) \end{aligned} \]

这样可以做到 \(O(n \log n)\)。但是实际上存在复杂度更优的解法。

首先是一个比较显然的式子：\(a = a * \mu * 1 = (a * \mu) * 1\)。这样方便我们导出整除。

\[\sum_{i=1}^n \sum_{j=1}^n A_i B_j \sum_{d | i, d | j} C'(d)\\ = \sum_{d = 1}^n C'(d) (\sum_{i=1}^{n/d} A_i) (\sum_{i=1}^{n/d} B_i) \]

其中 \(C'(n) = (C * \mu)(n)\)。

看起来还是 \(O(n \log n)\) 的，但是实际上可以更优。

抛出三个比较重要的模型：

\(B(n) = \sum_{d | n} A(d)\)（卷 \(1\)）：高维前缀和

\(B(n) = \sum_{n | d} A(d)\) ： 高维后缀和

\(B(n) = \sum_{d | n} A(d) \mu(n / d)\)（卷 \(\mu\)）：高维差分。

通过枚举每一维做可以做到 \(O(\sum_{p \in Prime} n/p) = O(n \log \log n)\)。

---

回到原问题。三个一起反演不好反演，可以先反演两个，提出去进行一波转化，转化得差不多的时候再反演第三个。

复杂度：\(O(n \sqrt n \log n \log\log n)\)，不知道怎么证成的 \(O(n \sqrt n \log \log n)\)。

Expected Square Beauty

一个长度为 \(n\) 的序列 \(a_i\)，其中 \(a_i\) 为 \(l_i ... r_i\) 的整数间均匀随机的一个随机变量。

称极长的值相同的子段为一个颜色段，求总共颜色段数的平方的期望。

\(1 \le n \le 2 \cdot 10^5,1 \le l_i \le r_i \le 10^9\)

首先考虑弱化版：求颜色段数的期望。考虑在一个段的开头计数，那么每一个点只有当其与前一个数不同的时候会产生贡献。设 \(p_i\) 为 \(P(a_i \not= a_{i-1})\)，\(q_i = 1 - p_i\)，那么答案为 \(\sum p_i\)。

考虑求平方的期望。有一个常用 trick 是：将某数的平方的期望转化为每个点对的贡献，于是答案为

\[\sum_{i=1}^n \sum_{j=1}^n P(a_i \not= a_{i-1} \wedge a_j \not= a_{j-1}) \]

注意到这个 \(P\) 大部分时候都等于 \(P(a_i \not= a_{i-1}) \cdot P(a_j \not= a_{j-1})\)，只有 \(|i-j| \le 1\) 的时候才会错，于是微调一下即可。

复杂度：\(O(n \log n)\)，瓶颈在求逆元，可以优化至 \(O(n)\)，但是没必要

逃跑

有 \(n\) 天，初始在 \((0,0)\)，每天会随机跑向旁边一格，跑到上下左右的概率为 \(w_1,w_2,w_3,w_4\)。

问跑到的不同的格子数 \(X\) 的方差 \(V(X)\)。

\(1 \le n \le 100\)

首先根据套路，\(V(X) = E(X^2) - E(X)^2\)，于是转而求 \(E(X)\) 和 \(E(X^2)\)。

首先考虑求 \(E(X)\)。设 \(f(i,j,k)\) 表示 \(i\) 天第一次到 \((j,k)\) 的概率，那么 \(E(X) = \sum_{i,j,k} f(i,j,k)\)。

设 \(g(i,j,k)\) 表示 \(i\) 天到 \((j,k)\) 的概率，这个不难求出。考虑 \(f,g\) 的区别：\(g\) 到 \((j,k)\) 后还会兜几圈子，于是有 \(G_{j,k}(z) = F_{j,k}(z) * G_{0,0}(z)\)，其中 \(G_{j,k}\) 表示 \(g(...,j,k)\) 的生成函数。暴力求逆可以做到 \(O(n^4)\) 求出 \(f\)，于是得到 \(E(X)\)。

考虑求 \(E(X^2)\)。根据套路， \(E(X^2)\) 可以拆成 \(\sum_p \sum_q P(同时到过 p,q) = 2\sum_{p<q} P(同时到过 p,q) + E(X)\)。于是只用考虑求 \(\sum_{p< q} P(同时到过 p,q)\)。

接下来是一个比较神奇的操作：设 \(h(i,j,k)\) 表示所有的 \((a,b)\)，\(i\) 秒（第一次） \((0,0) \to (a,b) \to (a+j,b+k)\) 的概率的和，那么答案就是 \(\sum_{i,j,k} h(i,j,k)\)。这个 \(h\) 可以通过容斥来递推：（注意是用 \(f\) 递推，否则会计重）

\[h(i,j,k) = \sum_{t < i,a,b} f(t,a,b) \cdot f(i-t,j,k) - \sum_{t < i} h(t, -j,-k) \cdot f(i-t,j,k) \]

优化后可以 \(O(n^4)\) 求出 \(h\)。

总复杂度：\(O(n^4)\)

Split

给定长为 \(n\) 的序列 \(a_i\)，需要构造一个长为 \(2n\) 的序列 \(b_i\)，使得 \(b_{2i} + b_{2i-1} = a_i\)，并且序列 \(b_i\) 的颜色段数尽量小。颜色段数为相邻相同元素合并后的序列大小，如 \(2,3,3,3,4,2,2\) 的颜色段数为 \(4\)。只需输出最小的颜色段数。

\(1 \le n \le 5 \cdot 10^5,1 \le a_i \le 10^9\)

比较巧妙的DP优化题。

首先考虑暴力DP。我们的目的肯定时要尽可能多地合并，于是设 \(f(i,j)\) 表示考虑 \(1...i\)，其中 \(b_{2i} = j\) ，的最多合并次数，最终答案为 \(2n - \max_j f(n,j)\)。

\[f(i,j) = [2 | a_i] + \max(f(i-1,a_i - j) + 1, \max_k f(i-1,k)) \]

这个DP可以被表述为：

1. 找出最大的DP值 \(mx\)。

2. 仅保留 \(1...a_i - 1\) 的DP值，将其余删除。

3. 所有 DP 值加 \(1\) 后对 \(mx\) 取 \(\max\)。

4. 若 \(a_i\) 为偶数，则 \(a_i / 2\) 处加一。

5. 翻转DP数组（\(dp_x \to dp_{a_i - x}\)）。

手玩发现，DP值的最大值的位置一定是 \(O(n)\) 个单点加上最多一个区间，我们可以用 set 来优化转移。

• 最大值位置被删光了：如果 \(a_i\) 为奇数，那么最大值位置为 \(1...a_i - 1\)，否则为 \(a_i / 2\) 且值+1
• 没删光，并且 \(a_i / 2\) 是最大值：最大值位置为 \(a_i / 2\)，值+2，可以删除其余位置（对以后没有影响）
• 没删光，且 \(a_i\) 为偶数：最大值 + 1，且 \(a_i / 2\) 加入最大值
• 没删光，且 \(a_i\) 为奇数：最大值 + 1.

最后翻转最大值位置即可，可以通过打标记（\(x \to a_i - x\)，\(k=1,b=a\)）来维护。

总复杂度：\(O(n \log n)\)。

Minimum Cost Paths P

有一个 \(N \times M\)（\(2 \le N \le {10}^9\)，\(2 \le M \le 2 \times {10}^5\)）的正方形方格组成的二维方阵（想象一个巨大的棋盘）。对于 \(x \in [1, N], y \in [1, M]\)，从上往下第 \(x\) 行、从左往右第 \(y\) 列的方格记为 \((x, y)\)。此外，对于每一个 \(y \in [1, M]\)，第 \(y\) 列拥有一个代价 \(c_y\)（\(1 \le c_y \le {10}^9\)）。

每次从方格 \((1, 1)\) 出发。如果现在位于方格 \((x, y)\)，则可以执行以下操作之一：

• 如果 \(y \lt M\)，那么可以以 \(x^2\) 的代价移动到下一列（\(y\) 增加一）。
• 如果 \(x \lt N\)，那么可以以 \(c_y\) 的代价移动到下一行（\(x\) 增加一）。

给定 \(Q\)（\(1 \le Q \le 2 \times {10}^5\)）个独立的询问，每个询问给定 \((x_i, y_i)\)（\(x_i \in [1, N]\)，\(y_i \in [1, M]\)），计算从 \((1, 1)\) 移动到 \((x_i, y_i)\) 的最小总代价。

很神奇的一道DP题。（好像还可以用保序回归做？）

一个显然的暴力DP是设 \(f(i,j)\) 表示从 \((1,1)\) 走到 \((i,j)\) 的最小代价，转移也比较简单。但是复杂度是 \(O(nm)\) 的，无法接受。

考虑一列一列地DP，尝试快速地从某一列转到下一列。

不难发现对于一列来说，代价关于行数的函数是个斜率逐渐增大的凸函数，因为越往下，竖着走的代价不变的同时横着的代价在猛增。一个维护凸函数的好方法是维护其差分数组。考虑相邻列的转移，如果只考虑横着走，那么代价函数是个二次函数，差分是个等差数列；再考虑上竖着走，那么手玩一下发现应该是代价函数后面部分可以改成一条斜率为 0 的直线。于是用单调栈维护一下即可。

细节比较多。比如这题只保证了最后答案不超过 \(10^{18}\)，但是没保证中间量不超过 \(10^{18}\)，这时候可以中间量使用 unsigned long long 运算，这样在模意义下答案始终是正确的。注意 unsigned long long 慎用除法。

总复杂度：\(O(n \log^2 n)\)

Cow and Vacation

\(n\) 个点的无根无权树，\(r\) 个中转点，每次可以跳 \(k\) 步，如果是中转点，可以继续跳 \(k\) 步。

\(q\) 组询问，每次给定 \(x,y\)，询问 \(x,y\) 是否相互可达。

\(1 \le n,q \le 2 \cdot 10^5\)

将边拆点，转化为 \(a,b\) 可达当且仅当与 \(a,b\) 相距 \(k\) 的点集有交，于是可以直接把与关键点相距不超过 \(k\) 的点用并查集合并。

判断 \(x,y\) 是否可达：如果 \(x,y\) 相距不超过 \(2k\)，显然可达；否则 \(x,y\) 各向对方走 \(k\) 步，然后查询 \(x,y\) 的并查集是否为一个点即可。

复杂度：\(O(n\log n)\)

芳

有 \(n\) 个矩形和 \(q\) 组询问，每个矩形带有一个权值 \(x\)，每组询问给定一矩形区域，问 \(n\) 个矩形中与这个矩形有交（有公共点）的权值的最大异或和。

\(1 \le n,q \le 30000\)

如果所有矩形均转化为一维，那么大致有两种做法：

1. 修改按左端点排序，询问按右端点排序，修改时贪心维护右端点尽量靠右的。复杂度 \(O(n \log n)\)
2. （适用于其它线段相交问题）如果两线段相交，那么一定存在第一个线段在线段树上的一个点和第二个线段在线段树上的一个点有祖先子孙关系。于是可以用类似标记永久化的写法写棵线段树。复杂度：\(O(n \log^3 n)\)

于是这个二维问题可以用这两种方法每种干掉一维。即：外层用第一种方法，内层用第二种方法。具体实现见代码

Wind of Change

给定两棵边权非负的树，对于每个点 \(i\)，求出一个 \(j \not= i\)，最小化 \(dis_1(i,j) + dis_2(i,j)\)。

\(1 \le n \le 250000,tl=12s\)

树上路径问题考虑点分治。

分别建点分树，对于每个点，枚举第一棵点分树上的祖先 \(anc_1\)，再枚举第二棵树上的祖先 \(anc_2\)，得到两个距离的和 \(d\)，共得到 \(O(n \log^2 n)\) 对三元组 \((anc_1,anc_2,d)\)。对于 \(anc_1,anc_2\) 相同的三元组，求出最小和次小，然后对每个点的 \((anc_1,anc_2,d)\) 贪心求值即可。复杂度：\(O(n \log^2 n)\)。

但是会被卡空间，于是可以先枚举 \(anc_1\)，然后再找出所有的 \((anc_2, d)\) 的三元组，这样就只有 \(O(n \log n)\) 对了。

Arkady and Rectangles

按顺序在坐标轴上画 \(n\) 个颜色为 \(1...n\) 的矩形（数字大的颜色覆盖数字小的颜色），问最后能看到多少种颜色。

\(1 \le n \le 10^5\)，坐标不超过 \(10^9\)

离散化后扫描线，线段树维护想要被看到，标号至少是多少，以及能看到的最大标号。set 维护完全覆盖每个点的矩形标号，每次取最大的更新信息。复杂度：\(O(n\log^2n)\)。

注意，扫描线要么先离散化后减一，要么先减一后在每个点后面再加一个点后离散化。否则会出现中间有一段被遗失的情况。

Clockwork Bomb

给出两棵n个节点的树，每次操作可以把第一棵树的一条边删掉然 后连另外两个点，且必须满足每次操作完之后仍是一棵树

问最少需要多少步操作才能把第一棵树变成第二棵树(是完全相 同,并不是同构),并输出方案

\(n \le 5 \cdot 10^5\)

如果可以先删掉若干条边，再一块连起来，那么答案显然是 $n-1 - $ 公共边数。我们现在尝试构造出这个下界。

先将公共边缩点，然后都以 \(1\) 为根，在第一棵树上 DFS，自底而上依次修正（换父亲）。

正确性依赖于一次出环的操作一定是将父边连向了自己的子树内，我们从叶子开始就规避掉了这种情况。

rplexq

给定 \(n\) 个点的树，\(q\) 次询问编号在 \(l...r\) 中且 LCA 为 \(x\) 的无序点对个数。

\(1 \le n,q \le 2 \cdot 10^5,ml = 128MB\)

充分考察了各种平衡复杂度的技巧。

有一个显然的做法：设 \(f(x)\) 为 \(x\) 子树中编号为 \(l...r\) 的点数，那么答案为 \({f(x) \choose 2} - \sum_{son} {f(son) \choose 2}\)，于是转化为求 \(f(x)\)，这是个二维数点问题，复杂度为 \(O(n d(n) \log n)\)，其中 \(d(n)\) 为儿子个数。

但是这道题并没有保证数据随机，我们不能让复杂度过多地与 \(d(n)\) 有关。解决这种问题的一种常用方法是 重链剖分（和这道题一样），对重儿子直接维护，每个点向上贡献给每个轻边连着的祖先。后者可以用莫队来解决，移动 \(l,r\) 的时候跳链；前者可以二维数点，最终复杂度为 \(O(n \log n + n \sqrt n \log n)\)。

这个复杂度还不是很平衡，于是可以考虑多维护一些儿子作为重儿子，比如维护 \(\sqrt n\) 个重儿子，这样每跳一次轻边树大小就会乘 \(\sqrt n\)，跳链次数为 \(O(1)\)，总复杂度变为 \(O(n \sqrt n \log n + n \sqrt n)\)。

还有一处可以优化的是，二维数点的时候有 \(O(n)\) 次插入和 \(O(n \sqrt n)\) 次查询，于是可以写一个 \(O(\sqrt n)\) 修改 \(O(1)\) 查询的分块，复杂度优化为 \(O(n \sqrt n + n \sqrt n) = O(n \sqrt n)\)，很平衡。

然而二维数点那里的空间复杂度是 \(O(n \sqrt n)\) 的，会 MLE，除非我们能够快速找到一对差分，直接算出组合数贡献给那组询问。注意到一组询问的询问矩形在编号维是相同的，在 dfn 维是挨在一起的，那么我们如果可以按照 dfn 维扫描，每组询问只需记录上一次的值，即可快速查出那个差分的值。这样空间复杂度优化为 \(O(n)\)。

然而会被卡常，可是复杂度看起来已经十分平衡了。不过考虑到二维数点常数较大（主要是枚举询问需要用到 vector），莫队常数较小，于是可以改为维护 \(100\) 个重儿子，然后就可以通过了。

Sunčanje

给定 \(n\) 个矩形，问每个矩形是否被编号比它大的矩形覆盖。覆盖一部分也算覆盖。

\(n \le 10^5\)

对于这种矩形覆盖问题，只要询问信息可加可减，都可以采用这种容斥的方法：

对于每个矩形，算出编号比他大且完全在它上面，下面，左面，右面的矩形个数，再减去上左，上右，下左，下右的矩形个数，即为编号比它大的与它无交的矩形个数。这分别是二维偏序和三维偏序问题。

复杂度：\(O(n \log n)\)。

Kangaroos

给定长为 \(n\) 的区间序列 \([l_i,r_i]\)，这里的区间指整数区间，区间 \([l,r]\) 包含 \(l...r\)。有 \(q\) 组询问，每组询问给定 区间 \([a,b]\)，要求找出最长的区间的区间 \([x...y]\)，使得 \([l_x,r_x],[l_{x+1},r_{x+1}]...[l_y,r_y]\) 均与 \([a,b]\) 有交。

\(1 \le n \le 50000,1 \le q \le 2 \cdot 10^5\)

序列多组询问区间问题的常见解法：莫队，扫描线，上二维平面。这里给一种莫队做法。

不难想到的是将线段的 \(l_i,r_i\) 看作点离散化，然后询问拓展一个点 \(p\) 会多出来以 \(p\) 开头或结束的线段。然后又要实时维护最长连续段，这个可以用线段树维护，但是太难写了；不如改成回滚莫队，上并查集在一个连续段的左右端点记录这个连续段的信息，方便合并不便删除。回滚可能需要一个可撤销数组。复杂度 \(O(n \sqrt n)\)（大致认为 \(n,q\) 同阶）。

然而这个做法是错的，只能过掉样例，因为这个做法没有考虑到跨越 \([a,b]\) （完全包含）的区间，导致答案偏小。于是想办法解决这个问题：对于零散询问（\(b-a \le B\)），先预处理出完全包含当前块（左端点所属块）的区间，然后每次暴力判断块内涉及到的所有区间，算完后回滚；对于长询问（\(b-a > B\)），预处理出跨越当前块和后面的块的所有区间，然后每次正常做回滚莫队。这样就能把所有完全包含的情况处理掉了。

细节较多。

总复杂度：\(O(n \sqrt n)\)。

Snuke the Phantom Thief

平面上 \(n\) 个点，坐标给定，每个点有价值 \(v_i\)。

\(m\) 条限制，每条限制为第 \(t\) 维坐标不小于/不大于 \(a\) 的点数不超过 \(b\)。

要求选一些点，求满足限制的最大获益。

\(n \le 80,m \le 320\)

首先直接费用流是不好限制的，因为限制“一个点符合多个限制，一个限制对应多个点”是很难做到的。

枚举答案，变成“前/后 \(r-b\) 个点坐标小于/大于 \(a\)”，这样就转化成点与限制区间之间的匹配关系。上三分图模型即可。

Wide Swap

给定一长为 \(n\) 的排列，对于 \(i < j\)，如果 \(j-i \le K\) 且 \(|p_i - p_j| = 1\)，那么可以交换 \(p_i,p_j\)。

求经过若干次交换后字典序最小的排列。

\(1 \le n \le 5 \cdot 10^5\)

首先可以交换排列的下标和值，问题变为 \(p_i,p_{i+1}\) 相差至少 \(K\) 的时候可以交换这两项，要求最终 \(1\) 的位置尽量靠前，然后在此前提下 \(2\) 的位置尽量靠前...

显然，\(p_i,p_j\) 相差小于 \(K\) 的 \(p_i,p_j\) 的相对顺序固定，那么我们猜想保证这些 \(p_i,p_j\) 的相对顺序不变的前提下，我们可以遍历所有可能的排列（感性理解好像是对的）。

如果 \(|p_i - p_j| < K,i < j\)，那么我们从 \(i\) 向 \(j\) 连边，这样会形成一张 DAG，我们要找到某种意义上“最小”的拓扑序，使得 \(1\) 的位置尽量靠前，然后在此前提下 \(2\) 的位置尽量靠前...

这种要求和 菜肴制作 完全一样，我们可以直接套用那道题的做法：倒着拓扑，每次选取 \(p\) 最大的扔到拓扑序的后面。

但是现在边数太多了，会 TLE。不过发现在 \(i\) 的时候，如果出现多个 \(j < i,p_j < p_i,p_i - p_j < K\)，那么这些 \(j\) 也会相互连边。而对于 \(a \to b,a \to c,b \to c\) 的DAG 来说，仅保留 \(a \to b, b \to c\) 这两条边的拓扑序的所有可能是一样的。于是我们只需要用权值线段树维护值域区间的位置最大值即可。

复杂度：\(O(n \log n)\)。

现在我们总结一下拓扑序的”字典序“最值（以最小为例）的相关内容：

如果”字典序“是真的字典序，即第一个数尽量小的前提下第二个数尽量小...那么我们可以正着拓扑，每次选取最小的一个放在拓扑序的前面。这个方法基本上就是完全模拟字典序贪心。

如果”字典序“是这道题的”字典序“，即最终 \(1\) 的位置尽量靠前，然后在此前提下 \(2\) 的位置尽量靠前...那么正着拓扑不好搞，因为说不准某个看起来比较大的点的后面藏着 \(1\)；但是倒过来拓扑把最劣的放后面肯定不劣，于是就可以倒过来搞了。

Jigsaw

一块拼图中间很高，高为 \(H\)，左右有两块可能悬空的部分，高度均不超过 \(H\)。共 \(n\) 块这样的拼图，要将它们拼一块，使得不存在“悬空”的部分（具体见原题面配图）

\(1 \le n \le 10^5,1 \le H \le 200\)

主要是左右“悬空”的部分不好搞，我们需要对每个悬空部分找到一个反向的对应高度的不悬空部分。一种方法是对每个悬空部分任意选，显然如果找不到的话就一定无解。

但是可能会出现连成环的情况，如下图：

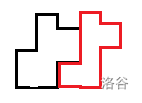
如何处理这种情况呢？

发现这种图其实可以从中间拆开，左右换个位置拼一块，拼完之后还是类似这种情况。我们可以选择一种拆法，重新拼完后将一个其它的块拆开，将这个块插进去，具体见下图：

每次成环暴力试看起来复杂度很高，我们可以在只剩下自己块对面的那个能跟自己拼的时候在去这么枚举，这样每种方向每种高度最多只会发生一次这种情况，于是最多只会发生 \(2H\) 次。并且这么做的话如果拆环失败就可以直接输出 NO 了。

实现的话比较麻烦，用并查集维护每个块；由于我们需要快速知道某个块外是否存在内部的某种特定的拼法，以判断是否能将那个块拆开把现在这个块塞进去，可能需要对每种拼法开个 set，并查集合并的时候对 set 也进行启发式合并。于是总复杂度为 \(O(nH + n \log^2 n)\)。

正解是欧拉回路，比较神仙。

Everything on It

有 \(n\) 个数 \(1...n\)。问有多少个集合的集合，满足每个数出现了至少两次。对大质数取模。

\(1 \le n \le 3000\)

显然二项式反演，转化为求 \(g_k\) 表示钦定某 \(k\) 个数出现不到两次的方案数。

首先仅由除了这 \(k\) 个数以外的其它数组成的集合是可以随便选的，最后乘上个 \(2^{2^{n-k}}\) 即可。于是只用考虑这 \(k\) 个数出现的集合的方案就好了。不难发现，这时集合个数 \(t\) 不超过 \(k\)，于是可以枚举 \(t\)。然后给每个数分到一组，共 \(t\) 组，可以有的数不分，最终给这 \(t\) 组随意配上其它 \(n-k\) 个数中的数，于是方案数为 \(S_2(k+1,t+1)2^{(n-k)t}\)，其中 \(S_2\) 为第二类斯特林数。

复杂度：\(O(n^2)\)。

Fib-tree

定义 \(k\) 阶斐波那契树为满足如下条件的树：

• 大小恰好为 \(Fib_k\)。
• 如果大小不为 \(1\)，则存在一条边，割掉后分为大小为 \(Fib_{k-1}\) 和 \(Fib_{k-2}\) 的两棵树。

给定一棵 \(n\) 个点的树，判定是否为斐波那契树。

\(1 \le n \le 2 \cdot 10^5\)

结论比较好猜，但是证明比较妙（也可能是我比较菜）。

结论：找到一条能分割成 \(Fib_{k-1}\) 和 \(Fib_{k-2}\) 的边，如果有两条，任选一条即可。递归判断。

证明：归纳法。当 \(n \le 3\) 的时候显然是对的。假设存在两条边，都能将数分割成 \(Fib_{k-1}\) 和 \(Fib_{k-2}\)，那么这棵树一定形如 \(Fib_{k-2}-Fib_{k-3}-Fib_{k-2}\)。此时假设割掉左边的边合法，那么对于右边部分割掉那条边也一定合法。于是这 \(Fib_{k-2},Fib_{k-3},Fib_{k-2}\) 都是合法的斐波那契树，随意割即可。

Yuezheng Ling and Dynamic Tree

给定 \(n\) 个点的树，满足 \(fa_i < i\)。\(q\) 次操作：

• 1 l r x ： 将编号在 \(l...r\) 的点的 \(fa_i\) 减 \(x\)，如果减到小于等于 \(0\) 则设为 \(1\)。
• 2 x y ：求 \(x,y\) 的最近公共祖先。

所有数不超过 \(10^5\)。

考虑类似重链剖分一样求最近公共祖先，但是由于链会边，我们需要找到一种不变的类似“重链”一样的东西。

对编号分块，记 \(g_i\) 表示从 \(i\) 开始往上跳，第一个跳出 \(i\) 所在块的点。分块维护 \(fa_i\)，每次暴力重构 \(g_i\)，当 \(tag\) 大于块长是不维护 \(g_i\)。

找 LCA 就模拟重链剖分即可，先跳到 \(g\) 相同，然后暴力跳。

复杂度：\(O(n \sqrt n)\)

Switch and Flip

给定长为 \(n\) 的排列，每次可以选择 \(i,j(i \not= j)\)，使得 \(a'_i \gets -a_j,a'_j \gets -a_i\)，即交换并取反。

要求在 \(n+1\) 次之内使得 \(a_i = i\)。

\(1 \le n \le 2 \cdot 10^5\)

需要比较精巧的构造能力和眼力。

首先将排列视为图论模型，\(i \to p_i\)，这样会形成若干环，最终目的为全搞成正数自环。

如果一个环上恰有两个负数，那么将一个负数位置 \(i\) 和其相邻的位置 \(i+1\) 交换后，发现位置 \(i\) 仍为负数且连向 \(i+2\)，\(i+1\) 成正数自环。这样我们能一步步消掉所有正数，最后交换两个负数就搞定了。

发现对于两个环，我们任选两个环内的两个点 \(u,v\)，交换 \(u,v\) 后两个环变为一个环且出现两个负数，然后就可以解决掉这两个环了。次数为 \(1 + (c_1 + c_2 - 1) = c_1 + c_2\)。

这样最终可以消完或只剩一个，如果还剩一个，那么随便拿过来一个不在环内的自环，看作两个环即可，只不过会多用一次，次数为 \(n+1\)。

然而，如果找不到那一个不在环内的自环，即存在一个大小为 \(n\) 的环，就不能用这个方法了。例如 \(2,3,1\)，经过手玩后发现，可以任选一个 \(i\)，交换 \(i,i+1\)，这样会出一个自环 \(i+1\)；然后再交换 \(i+1\) 和 \(i-1\)，发现有又并成了一个环，并且恰有两个负数。