最小割二元关系新解(lyd's ppt)
这一部分内容太多,故单独拿出来成为一篇文章。
问题描述:
有两个集合 \(S\) 和 \(T\),\(n\) 个元素。每个元素属于且仅属于 其中的一个集合。第 \(i\) 个元素如果属于 \(S\) 集合需要付出 \(A_i\) 的代价;属于 \(T\) 集合需要花费 \(B_i\) 的代价。
与此同时,还有一些二元组:\((x, y, C_1, C_2, C_3, C_4)\),表示:
-
如果 \(x\) 和 \(y\) 都属于 \(S\) 集合,需要 \(C_1\) 的额外花费 \(C_1\) 的代价;
-
都属于 \(T\) 集合,需要花费 \(C_2\) 的代价;
-
\(x\) 属于 \(S\),而 \(y\) 属于 \(T\),需要花费 \(C_3\)的代价;
-
\(x\) 属于 \(T\), 而 \(y\) 属于 \(S\),需要花费 \(C_4\) 的代价。
求最小代价。
模型建立
建立网络,如图:
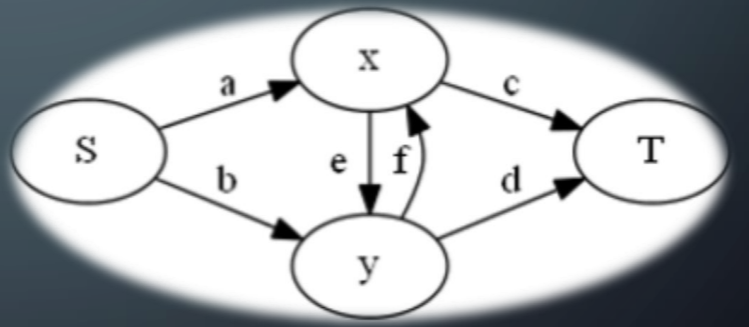
跑最小割。
最小割一共有四种形式 :
-
割边为 \(a\), \(b\),表示\(x\) 和 \(y\) 都属于 \(S\) 集合。最小割为 \(val_a + val_b\)。
-
割边为 \(c, d\), 表示 \(x\) 和 \(y\) 都属于 \(T\) 集合。最小割为 \(val_c + val_d\)。
-
割边为 \(a, d, f\), 表示 \(x\) 属于 \(S\) 集合, \(y\) 属于 \(T\) 集合。最小割为 \(val_a + val_d + val_f\)。
-
割边为 \(b, c, e\), 表示 \(x\) 属于 \(T\) 集合, \(y\) 属于 \(S\) 集合。最小割为 \(val_b + val_c + val_e\)。
(以下以 \(a, b, c, ...\) 来代替 \(val_a, val_b, val_c\))
有 :
通过控制 \(a, b, c, d, e, f\) 的数值来使得最小割的结果为正确答案。
为了简化问题,我们让 \(e = f\)。
设 \(K = C_3 + C_4 - C_1 - C_2\),则 \(e + f = 2 * e = K\),\(e = \frac{K}{2}\)。
此外,因为是网络流, \(a, b, c, d, e\) 按理来说都应该是正数。但是,有些不是正数就真的不行吗?
我们发现,对于每一种最小割,\(a, c\) 都被选且仅被选 一次,因此如果我们让 \(a, c\) 同时都加上 \(base\),那么答案就一定会加 \(base\),最后我们让答案减掉 \(base\)即可。
\(b, d\) 同理。
网络流模型中,我们常常用让一对被选且仅被选一次的边权值同时加上一个大数,最终答案再减去,来解决边权为负的问题。
现在,我们允许 \(a, b, c, d\) 为负,但是 \(e\) 不行。即:如果 \(K\) 为负数,则该问题无法用网络流的方法来解(至少我目前不行)。
总结一下 :
四个等式,五个未知数,可以有无数组解。
我们随意给 \(a\) 设置一个值,再推出其它所有未知数。
这种随意指定一个变量为某个不会影响答案正确性的值 的方法,也是 OI 中常用的思想。
得到 \(a, b, c, d, e\) 后,我们还可以把边合并一下(相同的边 权值直接相加),边数直接优化成与 \(n\) 相关,然后就可以直接跑最小割即可。
例题组Ⅰ
Dual Core CPU
【问题描述】的简化版。
设置 \(e\) 为 \(w\),直接跑最小割。
P1646 [国家集训队]happiness
题意:
文理分科。
班级为 \(n * m\) 矩阵,相邻(前后左右)为好友。每个人对文科和理科有自己的喜悦值,且一对好友如果同时选文或选理,又会使全班增添一些喜悦值(不同的好友喜悦值可能不同)。求全班的最大喜悦值。
\(n, m <= 100\),保证给出的所有数为非负整数。
正规的模板题应该是求最小值,而这道题要求的是最大值。那么我们把给的所有权值全部取负,就可以求最小值了。
这种将所有数取相反数,来实现“最大”“最小”的转化 的思想在 OI 中也经常用到,如:最大费用最大流,最长路等等。
然后我们已知 \(C_1, C_2\),并且 \(C_3, C_4\) 为零。就可以用上述方法解决了。
P4313 文理分科
题意:
文理分科。
班级为 \(n * m\) 矩阵,相邻(前后左右)为好友。每个人对文科和理科有自己的喜悦值,且如果他的所有 好友都和他选的文,又会获得一些喜悦值,都和他选的理,也会获得另一些喜悦值。求全班同学的喜悦值总和的最大值。
\(n, m <= 100\),保证给出的所有数为不超过 500 的非负整数。
仍然用相反数,将“最大”转化为“最小”。
这回要求周围人全部选同一种科,有些像下面的放石头那道题。因此我们新建一种点 \(cur_{ar}\) 和另一种点 \(cur_{sc}\)。如果选这种“新点”,就说明其周围的好友都选的文/理。当然,如果选这些点,我们要对其好友点进行限制,即禁止好友点选择另一种科目。即修改 \(C_3\) 或 \(C_4\) 为正无穷。
发现 \(K >= 0\),可行,直接用上面方法即可。
模型改进
发现模型只能解决 \(K >= 0\) 的问题。那么 \(K < 0\) 就真的不行吗?

如果我们把 \(x\) 和 \(y\) 之一的割的含义取反(即“割 \(a\) 表示选” 改为 “割 \(a\) 表示不选”),最终我们有:
(以取反 \(y\) 为例)
正好反过来了! \(K' = C_1 + C_2 - C_3 - C_4 = -K\) !
但是有一个问题,就是说 \(x\) 如果对于 \((x, y)\) 这个二元组来说取反,那么 \(x\) 对于其它形如 \((x, v)\) 的二元组来说也要取反。如果有 \((x, y), (x, z), (y, z)\) 都\(K < 0\),我们就无法一些元素含义取反了。(毕竟俩都取反就相当于没有取反)
因此,模型可行的要求进一步缩小为:所有 \(K < 0\) 的二元组不构成奇环。而我们恰好又经常在二分图里使用这个模型!
虽然 lyd 大佬是这么说的,但是我并不认同。比如:(二元组以 \((from, to, K)\) 的形式表示)
\((x_1, y_1, -1), (y_1, x_2, -1), (x_2, y_2, -1), (y_2, x_1, 1)\)
如果只要求符合前三条限制,那么 \(x_1\) 和 \(y_2\) 一定是含义不同的;而我们又要求 \(x_1, y_2\) 含义相同。因此是不可行的。而可怕的是,这四组关系是在二分图上的,并且 \(K < 0\) 的二元组甚至连环都没有构成!
因此,我将 用此方法可行 的条件修改为 : 如果存在一种方案,使得 \(K < 0\) 的二元组构成二分图,并且二分图左右部之间没有 \(K >= 0\) 的边相连,那么问题是有解的。
如何确定每个元素是否要对含义进行取反 ? 难不成为了判断这个来用一个匈牙利算法?(尽管复杂度是假的)实际上,我们可以充分发挥人类智慧 而不是机器力量 ,手动构建出二分图来。毕竟,一般来说我们的图还是有规律可循的。如果人类智慧实在不允许,dfs就可以了。(类似 2-sat 和 二分图?)
例题组Ⅱ
Topcoder SRM558 Div1 C Surrounding Game
题意: \(n * m\) 矩阵里放石头。在 \((i, j)\) 放石头要花费 \(Cost_{i, j}\) 的代价;在 \((i, j)\) 放石头或者 在其相邻的四个格子里放石头 会获得 \(Val_{i, j}\) 的收益。求总收益(收益 - 代价)的最大值。(所有数据均为正数)
收益 = -代价
然后求最小代价。
建立 \(2n\) 个节点。(除了原有网格 {\(cur\)} 外新建一组网格 {\(cur'\)})如果选 \(cur = (i, j)\),那么得到 \(Cost_{i, j} - Val_{i, j}\) 的代价。
如果选择 \(cur' = (i, j)'\),那么得到 \(Val_{i, j}\) 的收益,并且强制要求选择 \((i, j - 1), (i, j + 1), (i - 1, j), (i + 1, j)\),强制要求不选 \((i, j)\)(贪心)。
然后根据模型求解。发现“强制选择” 的 \(K\) 为正,“强制不选”的 \(K\) 为负,那么我们就要求 \(cur\) 和 \(cur'\) 不同时将意义取反,只取反一个;还要求 \(cur'\) 与相邻的 \(neibor\) 同时取反或不取反。
通过手动打表找规律,我们发现如果用红色表示取反,黑色表示不取反,那么整个网格 {\(cur\)} 和 {\(cur'\)} 是红黑相间的。
然后再充分发挥我们的码力,进行一堆判断,解决这道题。(事实上也不需要多少判断,毕竟每连一条边,最多只有两种情况)
拓展延伸
2-sat
(据说) 当所有权值为 1 时,此模型为 2-sat。
2-sat 问题我尚且没学懂,因此暂时搁一边。
证明最大权闭合子图的解法
最大权闭合子图:点有点权(可正可负),有一堆边,表示选择 \(x\) 就必须选择 \(y\)。求最大点权和。
再次搬出模型:

规定 : 与 \(S\) 连表示选择;与 \(T\) 连表示不选。(其实反过来也可以做)
将所有权值取反,来将“最大”转化成“最小”。那么选 \(x\) 不选 \(y\) 将付出 \(+∞\) 的代价。
那么我们将 \(f\) 设置为 \(+∞\),其余变量全部设置为 \(0\)。那么图上就只有 \(f\) 这一条边了。再加上只要选择就会拥有的权值(即 \(a, b, c, d\) 边)。
根据之前的方法,如果权值为负,那么两边同时加上绝对值,就可以转化成为正。
因此:如果权值为正,那么取反后权值为负,应该与 \(T\) 连权值为 \(w\) 的边;如果权值为负,那么取反后权值为正,应该与 \(S\) 连权值为 \(-w\) 的边。
最终我们的决定是:将 \(S\) 与负点连, \(T\) 与正点连,对于边\((x, y)\),连 \((y, x, +∞)\)。
将 与 \(S,T\) 连边的意义取反,那么我们的所有选择也应该倒过来,就是 : 将 \(S\) 与正点连, \(T\) 与负点连,对于边\((x, y)\),连 \((x, y, +∞)\)。
这就是一般的求最大权闭合子图的方法。
证明最大密度子图的改进算法
仍然考虑 01 分数规划后的那个要我们最小化的式子:
将 \(val_p\) 视为选择 \(p\) 的代价,不选代价为 0;\(val_e\) 视为一对二元关系:如果选择 \(u, v\) 两点,将会得到 \(-d * val_{u, v}\) 的代价。
列方程:
发现 \(K >= 0\),于是我们就可以愉快的直接套用模型了。
设置 \(a = b = -d / 2 * val_e, e = f = d / 2 * val_e\)。
然后直接求即可。
发现实际上 \(a\) 与 \(S\) 的连边的流量和为:\(-d / 2 * \sum_{(u, v)}val_{u, v}\),再加上最后的 \(val_u\),恰好为上文的 \(val[p] - d / 2 * sum[p]\)。边的流量也为 \(d / 2 * val_e\)。至于方案为什么是正确的,也很明了了。
例题组Ⅲ
P2805 [NOI2009]植物大战僵尸
最大权闭合子图裸题。
然后发现连样例都过不了。
因为最大权闭合子图是说,如果选 \(x\) 就必须选 \(y\),选 \(y\) 就必须选 \(x\),那么可以把两个都选上,也符合条件。但是本题并不允许“环”上的点被选(找不到突破口)。
因此需要先拓扑排序,排除掉无法被选的(包括环以及被环上的点所保护的植物),对于其它的植物建最大权闭合子图。
归纳总结
何时要注意取反,何时可以直接解方程?
我们发现,如果二元关系为:要求两个元素同时选或同时不选, 且代价为负数(获得正的收益),即 \(C_1, C_2 < 0\),\(C_3,C_4 = 0\),那么 \(K > 0\);
或者二元关系为:要求两个元素做出不同的选择,且代价为正数,即 \(C_1, C_2 = 0\),\(C_3,C_4 > 0\),那么 \(K > 0\);
这两种情况不用考虑取反的事情。
习题
上述提到的所有例题
CF1082G Petya and Graph
NOI 最大获利 重题,最大密度子图的简化版。最大权闭合子图、二元关系模型均可。
注意:\(base\) 的总和可能会很大(大概 \(1e15\)),但本题可以接受。如果遇到其他题要爆 \(long \ \ long\),就要灵活变通一下,不让每个点都去减 \(base\)。只需把边搞成 0 即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号