这里放一些我参加过的考试题和比赛题中没想出来的题（所以可能不仅仅是毒瘤的思维题，还有可能有简单的思维题以及窜进来的数学数据结构之类的题）。

还有一部分平时较难的练习题。

CF351E Jeff and Permutation

给出数组 $a$ ,你可以改变每个数的正负，求逆序对数最少是多少。$n \le 2000$

只想出来了 $n\le20$ 的暴力，根本没想贪心。

先不考虑绝对值相同的数。不易发现，如果我们只在较大数上统计贡献的话，在考虑绝对值最大的那个值的时候，其余数取正取负对其无影响。唯一有影响的是它的取正取负以及其左右数的个数。并且其取正取负，对剩下的子问题毫无影响。于是每次贪心决定取正取负即可。

对于存在绝对值相同的情况，我们完全可以不用管它。因为最终它们的决定一定是左边一段为负，剩余一段为负。

ARC104D - Multiset Mean

Given positive integers $N,K$ and $M$($N,K \le 100$) , solve the following problem for every integer $x$ between $1$ and $N$ (inclusive):

Find the number, modulo $M$, of non-empty multisets containing between $0$ and $K$ (inclusive) instances of each of the integers $1,2,3⋯,N $such that the average of the elements is $x$.

显然是个多重背包问题，然而当时我并没有发现。

利用多重背包的单调队列优化（或者前缀和优化），可以做到 $O(n^6)$；利用 CSP2019D2T1 的那种套路，对平均值做差值，最后查 $0$，可以做到 $O(n^5)$；然后发现这种方法实质上就是把小于和大于的元素分开，小于的数值翻转，大于的统一减当前值，然后再合并。合并前的操作发现就是背包，于是提前预处理，可以做到 $O(n^4)$。

由于数据不强，还给了 $4s$，$O(n^5)$ 算法可过。所以只要我想到优化$1,3$中的任意一种就能AC，但是我没想到（甚至连多重背包都没想到）/kk

CF1114F Please, another Queries on Array?

一开始给 $n$ 个数 $a_i$，然后要求支持两种操作:区间乘 $x$，查 $\varphi(\prod_{i=l}^ra_i)$。$n \le 4 \times 10^5,q \le 2 \times 10^5,1 \le a_i,x \le 300$

这题是真的水题啊，怎么就是想不出来啊/kk

一看到 $a_i,x\le300$，发现只有62个质数，于是我就对每个质数分别求解最后乘一块，树状数组维护区间加区间求和，然后就时空双双被卡了... 主要是卡时间，因为我每次询问都要查 62 次。并且一开始把 $a_i$ 的信息搞到树状数组中还费不少时间。

正确做法是$\varphi(p^c)=\frac{p-1}{p}p^c,c>0$，因此我们只需要区间乘，判断有哪些个数即可。这样就不用每次都查 62 次了。

CF382E Ksenia and Combinatorics

有多少种不同的大小为 $n$ 的二叉树，满足最大匹配为 $k$。不同指存在一个点的出边集合不同。$n,k\le40$。

也是个水题啊，为啥考试的时候就是不会啊

显然可以直接DP：

设 $f(i,j,0/1)$ 表示大小为 $i$ 的二叉树，最大匹配为 $j$，且根节点有没有被匹配。转移就枚举左右儿子的节点个数以及最大匹配数，然后 $0 \gets (1,1),1 \gets (0,1)/(1,0)/(0,0)$ 。这个其实就是树上贪心求最大匹配的方法。

值得注意的是，我们只考虑用当前节点匹配下面节点，不考虑留着当前节点来根父节点匹配的情况。这是因为贪心。有了这个，就不用取 max 了，所以一棵树转移是唯一的，不会计重。

但是由于这道题的判断相同的方式，我们直接用组合数硬搞会算两遍，于是最终除二即可。

CF1043F Make It One

给 $n$ 个数 $a_i$，要求选择尽量小的数，使得它们的 $\gcd$ 为1.$1 \le n,a_i \le 3 \times 10^5$

太水了...但是就是想不到反演

答案不超过 $8$，于是可以枚举答案 $k$，判定最后 $\gcd=1$ 的答案是否非零。$\gcd | n$ 的情况很好求，调和级数搞完 $h(n)=\sum_{n|i}cnt_i$ 后答案就是 ${ h(n)\choose k}$，于是直接反演即可。显然是莫反。

Two Permutations

给长为 $n$ 的排列 $a_i$，和长为 $m$ 的排列 $b_i$，求有多少非负整数 $x$，使得 $a_1 + x, a_2+x...a_n+x$ 为 $b_i$ 的子序列。$1 \le n \le m \le 2 \times 10^5$

没想到哈希...

显然 $a_1+x,a_2+x...a_n+x$ 的值域连续，因此我们可以将 $b$ 按值域排序，从小到大与 $a_1+x,a_2+x,...,a_n+x$ 比较，这样我们每次只用加入一个最大的数，删除一个最小的数，查 $b_i$ 的样子是否和 $a_i+x$ 一样。$b_i$ 与 $a_i$ 样子一样，当且仅当 $b_i$ 按其在原排列中的位置排序后的那个数组与 $a_i+x$ 数组完全一样，显然哈希可以做到。而插入删除可以用 Splay 或者权值线段树。

老园丁与小司机

一开始给一序列 $a_i$，并给一01串 $S$。现有两种操作：

修改：将 $a_l,a_{l+1},...,a_r$ 均异或上 $v$。

询问：给定 $l,r$，可以将 $l...r$ 中的一个数减小至任一非负整数（要求 $S_i=0$ 才能减少 $a_i$），减小后异或和的所有可能的值的和。

$n,m \le 10^5,0 \le v \le 10^9$

好神仙的一道NOIP题啊，不知道它们怎么想出来的。

考虑改一个数对区间异或的影响。如果这个数的第 $i$ 位为 $1$，那么它可以将这一位变为 $1$,前面的不变，后面的数就可以随便选了。对应在区间异或的影响就是 $i$ 位前不变，$i$ 位变化，$i$ 位后随意取。和为 $sum \times 2^i + S_1(2^i)$ ，并且所有的 $i$ 的这种贡献加一块就是全部的贡献。

发现无论是哪个数的第 $i$ 位为 $1$，其对答案的贡献是相同的。因此我们只需要维护区间内哪些位存在 $1$ 即可。可以用线段树维护区间或。

如果要区间取反的话，我们还需要知道哪些位是所有数均为 $1$，哪些位是一部分为 $1$。因此再记一个区间与。每次 pushdown 的时候对每一位讨论即可。而对于区间异或的维护就简单多了。复杂度：$O(n\log^2 n)$。

然后发现 pushdown 的那些讨论具有规律性，总结归纳后可以用位运算代替：（新）与 = ($v$ and (~或)) or ((~ $v$) and 与)；（新）或 = ($v$ and (~与)) or ((~ $v$) and 与)。复杂度：$O(n\log n)$

模积和

你需要找到所有的满足以下条件的二元组 $(x,y)$：

$l_1 \le x \le r_1$

$l_2 \le y \le r_2$

$l_3 \le |x - y| \le r_3$

$l_4 \le x \oplus y \le r_4$

其中 $\oplus$ 为异或.求 $\sum x \times y \bmod 998244353$

$0 \le l_i \le r_i \le 10^{15}$

弱化版

又是个毒瘤码农题。（为啥ywy出这么多细节题啊/kk）

看这数据范围除了数位DP也没啥别的了。首先一步容斥转化成 $l_i = 0$ 的问题；然后一步分类讨论转化为 $x \ge y$ 的问题（可能需要用自然数幂和清楚多算的 $x=y$ 的部分）。因为有位运算，只能是二进制下的数位DP了。于是我们可以设状态 f(cur,lx,ly,lxy,xy,xr) 表示从高往低要考虑第 $cur$ 位，$x,y,x-y$ 是否卡上限，$x$ 是否恰好等于 $y$，$x \oplus y$ 是否卡上限。然后枚举当前位的 $x,y$ 选啥，大力讨论转移即可。

然后发现会出错。因为 $lxy$ 这个状态是不够的，有时候当前看起来 $x-y$ 超出了上限，但是下一位一个借位，使得 $x-y$ 又回到了上限之内。比如上限为 $01$，$x=10,y=01$，第一位 $x-y$ 还在超出上限，看到第 $0$ 位就发现其实 $x-y$ 没超出上限。幸运的是，这种通过借位使得不合法变合法的情况只发生在之前 $x-y$ 只超了 $1$ 的情况下，超过 $2$ 就无论如何也不能将不合法变合法了。于是多记个 $lxy'$ 表示 $x-y$ 是否只超过上限 $1$：f(cur,lx,ly,lxy,lxy',xy,xr)。然后大力讨论判断转移即可。

然后发现还是错。因为题目要求模积和，而我们只求了方案数。那好，我们就记一下 $\sum x\times y$ 是多少。但是转移的时候可能会将之前的 $\sum x \times y$ 变成 $\sum (x + d) \times (y + d)$。不过拆开式子：$\sum xy + (x+y)d + d^2$。于是在记一下 $x,y$ 的和以及方案数即可。

复杂度：$O(\log n)$。但是常数大概有几万（容斥有 $2^4$，七维状态的后六维有 $2^6$，转移有 $2^2$，判断合并大概有十几）

std 用的是从低到高位的数位DP，比较奇怪。std的状态只有六维，并且写的是迭代，但是不知道为啥比我慢四倍。

游戏

A 和 B 玩游戏。现有 $n$ 个串，每个串长均为 $m$，且 A 和 B 都知道这些串是什么。现 A 等概率选择一个串让 B 猜。B 每次会在之前没询问过的位置中等概率选择一个位置来询问，A 会回答那个位置的字符。当某一时刻 B 能够确定是哪个串的时候，游戏停止。求 B 的期望询问次数。

$n \le 50,m \le 20$

这数据范围肯定要 $n2^m$ 的算法（尽管 std 是 $O(\frac{nm2^m}{w})$ 的）

考虑状压。显然的 $nm2^m$ 的状压就不再细说了。现考虑对所有 $n$ 一块考虑。

我们设 $f(S)$ 表示当前状态为 $S$，只考虑还不能确定的答案串，的期望询问次数。$g(S)$ 表示当前状态为 $S$，还不能确定答案的答案串个数，那么有：

\[f(S) = 1 + \sum_{T = S + i}\frac{1}{ct_0} \times \frac{g(T)}{g(S)} \times f(T) \]

~~tbl模式警告~~

（以下自动理解为随机游走模型）两个概率分别是当前走到 $T$ 的概率和（现在所有答案串都已经向前走了一步了）走到 $T$ 后仍能继续走下去的概率（因为 $f(S)$ 的前提是只考虑还不能确定的答案串）。因为所有能够走到 $S$ 的答案串都是等概率的（显然，因为询问次数相同），所以这个（第二个）概率是对的。

~~tbl模式警告结束~~

于是我们现在的问题为算 $g(S)$。我们可以枚举每个答案串，如果 $S$ 能够排除掉其它所有的串，那么 $g(S)$ 就不加，否则加一。于是我们可以记录 $h(S)$ 表示对于当前枚举的这个答案串来说，询问 $S$ 后能排除的串的集合。转移可以通过 lowbit 取并转移，如果只剩一位了的话可以预处理（或暴力算）。

复杂度：$O((n+m)2^m)$

2020.10.16 NOIP模拟赛 T2

给定一棵 n 个点的有根树，节点编号为 1~n，根节点为 1，满足每个点的儿子个数为 0 或 2 个。Alice 和 Bob 在这棵树上玩游戏，Alice 控制了所有到根距离为偶数的非叶节点，Bob 控制了所有到根距离为奇数的非叶节点（距离就是两点间的边数）。

游戏开始时，每个叶子节点 u 都会被分配一个二元组 $(c(u),d(u))$，c 和 d 均为 $[1,k]$中的正整数。接下来 Alice 和 Bob 会分别对他们控制的每一个节点指定一个重儿子，显然从根节点顺着重链会走到唯一一个叶结点$x$，这时 Alice 的得分为 $c(x)$,Bob 的得分为 $d(x)$。称两人的一种选择方案为一种策略，设叶子结点有 $l$ 个，显然策略有 $2^{n-1}$ 种。

定义一种策略是均衡的，当且仅当 Alice 不改变方案时，Bob 无论怎么改变自己的方案都无法使自己的得分变大；且 Bob 不改变方案时，Alice 无论怎么改变自己的方案也无法使自己的得分变大。请问对于所有合法的初始叶结点权值，均衡的策略的个数总和是多少？答案对 998244353 取模。

$n,k \le 5000$

考场上差点想到正解，只可惜没想到只有根伸向叶节点的重链确定的时候二者之间的互相限制才是独立的，否则可能都汇不到一个叶节点上。

我们可以枚举根伸向叶节点的重链，然后A对B的限制和B对A的限制就是完全独立的了。

现仅考虑A对B的限制，最终合并即可。然后我们需要保证B不会在这条链中间溜走，因此我们还需要保证重链旁边的这些轻链不会让B获得更大的收益。

我们可以预处理出 $g(x,i)$ 表示仅考虑子树叶节点中 B 的权值以及子树中 A 的决策，B选择最优策略，无法获得超过 $i$ 的收益的方案数。

当这个点由 A 控制的时候，A可以选择向左或向右，分别对应着 $g(u,i)*g(v,k)$ 和 $g(u,k) * g(v,i)$，其中 $u,v$ 为左右儿子。当这个点由 B 控制的时候，就只能要求两边都不超过 $i$，即 $g(u,i) * g(v,i)$。叶节点 $g(u,i)=i$。于是可以预处理出 $g$。

然后我们把那条链上的所有轻边的 $g$ 根据是否是 A 控制来判断到底是乘 $g(x,k)$ 还是 $g(x,i)$，暴力乘一下即可。发现复杂度有些危险，于是可以设 $f(x,i)$ 表示从根走到 $x$，旁边的 $g$ 的积。于是可以 $O(nk)$ 地搞了。

对 B 控制 A 也做类似的操作，然后再在每个叶子上将总方案数对应相乘再相加即可。

复杂度：$O(nk)$

其实还可以做到 $O(n^2)$.

设 $f(x,i,j)$ 为 $x$ 的子树中有 $i$ 个 Alice 可以到达的点，有 $j$ 个 Bob 可以到达的点。那么对于一种固定的局面，我们可以枚举直达的叶子的权值 $w,w'$，那么这个叶子有 $1$ 种方案，对于 $c$ 有 $i$ 个叶子有 $w$ 种方案，剩下的有 $k$ 种方案。Bob 同理。这里大概是个自然数幂和。

$f$ 关于 $i,j$ 是独立的，于是可以分开算。最后枚举 $i$，枚举 $j$ 统计答案。

2020.10.18 NOIP模拟赛 T4

给一高度数组 $a_i$，定义 $f_i$ 表示 $1...i$ 的单调减的单调栈的高度集合与 $i...n$ 的单调增的单调栈的高度集合的并再扣掉 $a_i$ 后的集合的大小。两种操作：

交换 $a_x,a_{x+1}$。

查询 $\sum_{i=l}^r f_i$

$n,q \le 2 \times 10^5$

普通线段树可以通过线段树上二分来找 $i$ 之前大于等于 $a_i$ 的前驱！这是线段树的基本操作啊，为啥考试的时候想不到啊qaq

首先考虑不交换的情况。这个比较水，对 $a$ 建一棵笛卡尔树，边权为俩点高度是否相等，然后 $f_i$ 就是 $i$ 到跟的距离。

现考虑交换操作。不易发现，$f_i$ 可以由大于 $a_i$ 的前驱后继中较小者转移，若 $l_i$ 高度比 $r_i$ 小，那么 $f_i = f_{l_i}+1$。于是如果我们能够维护出新的除了 $x,x+1$ 外的位置的 $f$ 值的话，就可以快速地求 $f_x,f_{x+1}$ 了。

显然当 $a_x = a_{x+1}$ 的时候答案不变。现仅考虑 $a_x < a_{x+1}$ 的情况，另一种情况类似。我们找出它俩两边 $a_j < a_x$ 的 $j$，分界点为第一个 $a_k \ge a_x$ 的 $k$。那么可以通过判断 $a_k$ 是否等于 $a_x$ 来进行转移。这部分比较好想，就不多说了。

复杂度：$O(n+q\log n)$

Bracket Score

给定两个长为 $n$ 的序列 $A_i$ 和 $B_i$，要构造出包含 [,],(和)的合法括号序列，对于第 $i$ 个位置，若其位置上的括号为 ()，那么价值为 $A_i$。否则为 $B_i$。要求总价值最小。输出总价值。

$n \le 10^5$

可能是这篇博客里面唯一一道自己想出来的题。但是大概想了俩小时，还是 lsr 说贪心可做我才开始使劲想贪心的，否则可能就死在DP上了。

显然有个 $n^3$ 的区间DP。还有，考虑到任何时候栈内一定像 ([([([...，于是可以压一下后 $n^2$ DP。然后就再也DP不动了。

考虑贪心。我们先把序列全选为 ()，获得 $\sum A$。现在我们可以将一些 () 变成 [] 并获得更大收益。手玩发现只要我们将一个相隔奇数位置的圆括号变成方括号，那么一定存在一组合法括号序列。于是将奇数位置和偶数位置的收益从大到小排序后贪心选即可。

复杂度 $O(n)$。

皇后游戏

给定 $n$ 个二元组 $(a_i,b_i)$，定义一个二元组序列中第 $i$ 个二元组的代价为 $c_i = max(c_{i-1},\sum_{j=1}^ia_j)+b_i$。特别地，$c_1 = a_1 + b_1$。要求将 $(a_i,b_i)$ 排序，使得 $\max_{1 \le i \le n} \{ c_i \}$ 最小。

多组数据。

$n \le 5 \times 10^5,T \le 10$

~~考试包括洛谷数据水，被我用五个 cmp 取 min 给水过去了/cy~~

邻项交换法贪心，不会。

现在不懂为啥让每个 $c_i$ 最优就能够让 $c_n$ 最优。

排序

给定一序列 $a_i$，有 $m$ 次操作，每次给定 $p$，要求把 $p$ 及其之后的 $ \le a_p$ 的数拿出来排序再放回去。如 1 4 2 5 3 ， $p = 2$ 的操作会拿出 4 2 3 ，排序再放回去后序列变成 1 2 3 5 4。

每次操作后输出序列的逆序对数。

$n,m \le 5 \times 10^5,a_p \le 10^9$

可能是我没做出来的最水的题了吧，这题明明人均切的啊qaq

可以在较大数上统计贡献。发现一次操作相当于将其右边 $\le a_p$ 的所有数的贡献清空，而其余的贡献不变。于是线段树维护区间最小值及其位置即可。复杂度 $O(n\log n)$

眼泪

对于一序列 $a_i$，两个人博弈。初始区间为 $l...r$，每次每个人可以删除区间的左端点或者右端点，最先将区间删成单调不降的人获胜。特别地，如果初始区间就已经单调不降了，那么认为后手获胜。

现给定一序列 $a_i$，以及 $q$ 次询问，每次问初始区间为 $l...r$ 的时候是谁获胜。

$n,q \le 10^6$

暴力比较好想，直接设 $f(l,r)$ 表示 $l...r$ 先手还是后手获胜。

然后我们可以把 $f(l,r)$ 放到二维平面上(我也不知道是咋想到的)，$l$ 为横坐标，$r$ 为纵坐标。我们可以预处理出 $g(i)$ 表示以 $i$ 为左端点，最靠右的合法区间的右端点是什么。然后在平面上这个 $g(i)$ 可以组成一些线段，可以连成一条折线。折线及其下面的都为 $0$，删除左/右端点相当于向右/上走（可以看作公平组合游戏的DAG图）。发现除了那条折线周围有两圈特例，其余的 $l+r=k$ 的 $f(l,r)$ 都是相同的。于是可以 $O(n)$ 预处理 $O(1)$ 查询。

总复杂度：$O(n+q)$

Equal Product

给定 $n,m,l,r$，定义合法四元组 $(x_1,y_1,x_2,y_2)$ 需要满足如下条件:

$1 \le x_1 < x_2 \le n$

$1 \le y_2 < y_1 \le m$

$x_1 \cdot y_1 = x_2 \cdot y_2$

$l \le x_1 \cdot y_1 \le r$

对于每个 $x_1$，构造一组合法四元组或判无解。

$1 \le n,m \le 2 \cdot 10^5,1 \le l \le r \le n \cdot m$

这题实际上就是要求合法的 $x_1 \cdot y_1 = x_2 \cdot y_2$。其中 $x_1 < x_2$，并且有若干范围上的限制。

显然枚举三个就可以求出剩下的那个。我们可以尝试再减少一些枚举量，只枚举 $x_1,y_1$，能不能构造出 $x_2,y_2$。不难想到，$x_2 = x_1 \times \frac{a}{b}$，$y_2 = y_1 \times \frac{b}{a}$。其中 $a > b,b | x_1,a | y_1$。然后我们发现 $a,b$ 也是很重要的参数，如果我们知道 $x_1,y_1,a,b$，就可以知道这个四元组。并且还有个看起来很有用的性质：$(x_1,b)$ 只有 $O(n \log n)$ 对。于是我们可以尝试枚举 $(x_1,b)$，然后再快速求出 $y_1,a$。当我们枚举好 $(x_1,b)$ 以后，我们能够得到一些关于 $y_1,a$ 的限制：$y_1 \in [\frac{l}{x_1},\frac{r}{x_1}],y_1 \le m,b < a \le b \cdot\frac{n}{x_1},a|y_1$。这就相当于给俩区间，要求在这俩区间内分别找出俩数，使得一个数是另一个数的倍数。由于 $a$ 的倍数只有 $O(m \log m)$ 个，于是我们可以去找最小的 $a$，将对 $a$ 的限制区间按左端点排序，线段树支持单调修改，线段树查询区间最小值，判断是否合法。

复杂度：$O(n\log^2 n)$

K Paths

$n$ 个点的树上选 $k$ 条路径，要求至少有一条边被全部经过，并且每条边被经过次数只能为 $0,1,k$。

问方案数。路径有标号。

$2 \le n,k \le 10^5$

CF原题:对 $998244353$ 取模

模拟赛题：对 $10^9 + 9$ 取模

最终的那 $k$ 条路径一定会形成一个公共链和链两段伸出的一些链。枚举公共链，链两段独立，分别考虑。对于每个点作为链端点的贡献为$f(i)$，设在子树中选择 $i$ 条子树，方案为 $F(i) = \prod siz_j \times {k \choose i} \times i!$，那么最终 $f(x) = \sum_{i \le k}F(i)$。这个有些类似背包，可以用DP预处理。复杂度 $O(\sum d^2)$。剩下的“枚举链”的那部分操作可以一遍DFS解决。复杂度 $O(n)$

但是发现有些“直上直下”的公共链可能还要求的是“有一个子树不能选，能选父亲”的方案数。这个可以额外预处理个 $g(x)$，表示 $x$ 的父亲，不能选 $x$ 可以选祖先的方案数，类似背包地计算一下。复杂度：$O(\sum d^3)$。

发现一个菊花图就直接没了。但是背包明显可以用多项式优化一下，可以用分治+多项式乘法优化求 $F$，复杂度变为 $O(\sum d \times \log^2 n)$。而那个 $g$ 可以在上面一下子考虑所有子树的 $g$。发现限制与 $F$ 的区别仅是不能选某一个，可以选其它的，然后统一乘一个二项式。这个也可以用分治+多项式乘法优化到 $O(\sum d \times \log^2 n)$。实在不行可以看代码。

模拟赛题可能需要用到 MTT，但是不知道为啥大数据点会RE，反正很毒瘤就对了。

代码里面封装了一些非固定大小的多项式（抄的 ZRQ 的），否则多项式开不下。用vector实现的，可以参考一下。

Omkar and Last Floor

有一个 $n \times m$ 的矩形，每一行被分成若干段，现需要向里面填数，只能填 $0,1$，且每一段只能填一个 $1$。

设 $q_i$ 表示第 $i$ 列的 $1$ 的个数。求 $\sum q_i^2$ 的最大值。

$1 \le n,m \le 100$

算法简单好写，就是不好想。

如果设 $f(i,...)$ 表示考虑完前 $i$ 列，如何如何，的最大值的话，除非我们状压哪些列填过数了，否则我们并不能准确地知道到底哪些列还能填数，哪些列不能。

只能换一种思路了。贪心地想，我们每次肯定是从 $1...m$ 中选择一列，尽可能地填数，填 $n$ 个数，然后将整个问题分成两个子问题。如果不是这样，即没有一列全部填数，那么我们可以从填得最多的那一列中找出没有填的数，找出那个数所在段的填的数的位置，那么我们把那个段的填数方案改成填到那一列不会更列。因为当前的 $q$ 更大些，他到当前列的贡献会更多些。

有了第一步，剩下的就都好说了。区间DP。我们设 $f(l,r)$ 表示完整包在 $l...r$ 中的段的最大贡献。随便转移一下就好了。

复杂度：$O(n^4)$。当然想优化到 $O(n^3)$ 也不难，但是 $n^4$ 已经足够了。

Omkar and Modes

交互题。

现有一个长为 $n$ 的单调不降的序列 $a_i$ 要我们猜。

每次可以询问 ? l r，返回 $l...r$ 的众数及其个数。

要求在不超过 $4k$ 次询问后还原出序列 $a_i$。其中 $k$ 为序列中值的种类数。

交互题就是不好想啊。

显然，一个值的位置是一段区间。如果我们能搞出区间众数 $x$，出现次数 $ct$，以及其中一个 $x$ 的位置 $p$ 的话，再来两次即可，两次分别是 $p...p + ct$ 和 $p-ct ... p$。

现在我们可以问一次 $1...n$，找出众数 $x$ 和出现次数 $ct$，但是不好找 $x$ 的位置 $p$。一种做法是：将 $ct,2ct,...$ 一个一个的查，一直到是 $p$ 的时候就可以干掉 $x$ 了。显然，这些位置上的数都是互不相同的。因此，我们不仅找到了 $x$ 的一个位置，还额外找到了好多其它的数的位置。现在我们需要保证每个数只被找到一次，这样的话次数就有保证了。

进入子问题 $1...n'$ 的时候，我们照样现查众数和出现次数。如果众数 $x$ 的位置已经被找到过，那么就好办了。如果没有找到，那么我们可以 lower_bound 出来 $x$ 的可行区间，在这个区间内的第 $ct,2ct,...$ 处查，一直到查到 $x$ 位置。显然，这些数是互不相同的，并且第一个数与前面的数不同，不存在与后面的数相同的数。于是我们就可以保证不会查到相同种类的数了。查询次数：最多 $4k$。

还有一种不太好想的方法：每次查全局的众数及次数，假设众数出现次数足够多，那么在 $r-ct+1...l+ct-1$ 中的数一定全是 $x$。那么我们可以递归到 $l...r-ct$ 和 $l+ct...r$ 中。

这种方法的查询次数不太好证。设 $T(n)$ 表示有 $n$ 种数的区间的最多的查询次数。那么：

\[T(1)=1,T(2)=3\\ T(n) = 1 + \max_{i+j \le n + 1}(T(i) + T(j)) \]

打表可知前几项：$T(1)=1,T(2) = 3,T(3)=7,T(4)=11,T(5)=15,T(6)=19,T(7)=23...$。我们猜测，对于 $n \ge 2$，有 $T(n) = 4n + 5$。那么 $T(n) = 1 + 4i-5+4j-5=4n-5$。

Reverse Binary Strings

给定一个长度为偶数的 $01$ 串，每次可以选定一个子串进行翻转操作。要求最后翻转成一个 $0,1$ 交替的串（只有 $101010...$ 和 $010101...$ 类型的串是合法的串）。求最少的操作次数。保证有解。

$n \le 10^5$

想不到我竟然被卡在了Div2B上/kk

看到 $101010$ 这样的交错 01 串，要想到差分。它的差分数组是 $111111...$ 或者 $01111111$。

然后考虑翻转操作。一次翻转操作最多会将两个 $0$ 变成 $1$，并且我们总可以找到这样的操作:在差分数组上找到一个 $1$ 段，在原数组上将这一段翻转，会发现少了俩 $0$。

因此，答案应该为 $\lceil \frac{ct}2 \rceil$。其中 $ct$ 为差分数组中 $0$ 的个数（第一个除外）

Make It Increasing

给你一个数列 $a$ ,一个集合 $b$ , 对于每个 $b$ 中的元素 $x$，$a_x$ 不能修改，其他都可以修改，问最少多少次可以将 $a$ 修改为严格单调递增的。如果不存在，输出 $-1$ 。

$a$ 中的所有元素在任意时刻必须都是整数。

$n \le 5 \times 10^5 ,0 \le k \le n,0 \le a_i \le 10^9, 1 \le b_1 < b_2 ... < b_k \le n$

严格单调递增不是很好搞（不过我赛后和thecold探讨出来了一种线段树优化DP的$O(n \log^2 n)$ 的做法），但是如果只是要求单调不降的话就可以找出最长不下降子序列，然后剩下的就可以随便修改了。于是可以让每个 $a_i$ 都 $+i$，然后搞类似 LIS 的DP即可。可以用树状数组优化。

Boboniu and String

对于一个 01 串 $s$，有四种操作：

删去一个 $0$ 或 $1$ 子串

删去一个 $01$ 或 $10$ 子串

在末尾加入一个 $0$ 或 $1$

在末尾加入一个 $01$ 或 $10$

定义两串是“相似的”，当且仅当俩串的 $0$ 和 $1$ 数量相同。

定义两串距离为将两串搞成相似的串的最小操作次数。

现有 $n$ 个串 $s_i$，需要构造出一个串 $t$，使得其与所有串 $s_i$ 的距离的最大值最小。

$n \le 3 \cdot 10^5, \sum |s| \le 5 \cdot 10^5$

显然串的具体样子并不重要，我们只需要知道串中 $0$ 和 $1$ 的个数。

接下来是神奇的一步:将 $0$ 的个数视为 $x$ 轴；将 $1$ 的个数视为 $y$ 轴，那么一步以内能走到的点为一个正方形除去两个角。走 $n$ 步以内能走到的点为边长为 $2n$ 的正方形除去俩角。我们可以用线性规划的方法来表述走 $l$ 步能到的区域：

\[x_0 - l \le x \le x_0 + l\\ y_0 - l \le y \le y_0 + l\\ x_0-y_0-l \le x_0 - y_0 \le x_0 - y_0 + l \]

当然，题意还有俩限制:

\[x,y \ge 0, x + y > 0 \]

这样，我们可以二分距离 $l$，判断是否有交即可。

（以上为比赛题中没想出来的题）

（以下为做题时思维难度较高的题）

寻宝游戏

给 $n$ 个长为 $m$ 的01串，多次询问通过在每个01串上插 & 或 | 运算符（最上面补个0）后运算结果为某个给的01串的方案数。 $n,q\le 1000,m \le 5000$

对于每一位分开考虑。显然如果最后 $\&0$ 或者 $|1$ 的话，我们就可以直接知道结果了；否则就需要继续向上找。而这个过程有些像我们写的高精比大小。于是我们可以把运算符也看作一个01串，根据经验，我们设 & 为1，|为0，然后将运算符串和它给的那些01串的那一位组成的串比较，如果运算符串大就是 $1$，小或等就是 $0$。于是问题转化为了不等式组的解数。

需要注意的是，不开 O2 的情况下不要用 bitset 代替 bool 数组！它的遍历的速度比 bool 慢好几倍！（尽管空间较小）因此如果不开 O2 的话最好的选择应该是手写 bitset，然后就可以做到复杂度除以64了。不过可能比较难写。

Number of Multisets

You are given two positive integers $N$ and $K$. How many multisets of rational numbers satisfy all of the following conditions?

The multiset has exactly $N$ elements and the sum of them is equal to $K$.

Each element of the multiset is one of $1,\frac{1}2,\frac{1}4, \frac{1}8 ...$ In other words, each element can be represented as $\frac1{2^i}(i=0,1,...)$.

$1 \le N,K \le 3000$

怎么又挂在了 Multiset 的数数题啊...

还是分治思想运用得不够熟练

考虑 $f(n,k)$ 表示 $N=n,K=k$ 的答案。考虑一共有两种情况：

不存在任何一个 $1$。此时相当于要达到的值扩大两倍：$f(n,k)\gets f(n,2k)$。
存在至少一个 $1$。此时我们把一个 $1$ 提取出来，剩下的是一个 $N=n-1,K=k-1$ 的子问题。即：$f(n,k) \gets f(n-1,k-1)$

看起来那个 $f(n,k) \gets f(n,2k)$ 好像会无限递归，但是当 $k > n$ 的时候有 $f(n,k) = 0$，于是不会递归到 $k > n$ 的情况。

复杂度：$O(n^2)$。

Mousetrap

树上管理员逼老鼠进陷阱房。老鼠后手，每个时刻必须沿树边走一步，除非无处可走，走后边被弄脏，无法走。管理员先手，每个时刻可以擦干净一条边，或者堵住一条边，或者不操作（不计入总次数）。问最优策略下管理员最少需要操作几次。老鼠的目标为尽量拖延时间。$n \le 10^6$。

要是我在考场上遇到这题，估计连min-max对抗搜索都写不出来。

考虑部分分：老鼠的起始点与陷阱房（看作根）相邻。此时一定是老鼠向下挑一个最优的子树跑下去，一直跑到底，然后动不了，等着进陷阱房。而管理员一定是尽量阻止老鼠进入最优的子树，等老鼠动不了的时候管理员再把老鼠到根的路径上的其它分支堵住，然后再放老鼠进陷阱房。于是老鼠只能跳次优的子树跑下去。

如果设 $s_i$ 表示 $i$ 到根的主干+分支的边数和（不含 $i$ 到儿子的边），$f_i$ 表示一旦老鼠进入 $i$ 个子树（认为上面到根的路径全脏了），管理员先手，管理员所需的最小操作次数。那么有:

\[s_y=s_x+du_x-1\\ f_x=s_x,x ~is ~a ~ leaf\\ f_x=s_x,x~ have~ only~ one~ son\\ f_x = secmax(f_y)\\ \]

然后 $f_s - 1$ 即为答案（最上面那条边不用擦）

现在考虑普遍情况。老鼠可能还是向下钻到一个子树里面，但是还有可能会向上跑一段距离，然后钻到一棵更优的子树中去。而这一段时间管理员的操作就不好确定了，因为我们并不知道管理员会不会堵住某些边。但是发现管理员的操作次数是有单调性的，于是我们可以二分管理员的操作次数，强制要求其在这些次数内能够把老鼠逼到陷阱房中。这样，我们就知道每条连向子树的边是否要堵了。如果钻进去以后剩余操作数不够了，那就必须堵住，否则就留着操作次数以后用。另外，需要对一开始是否要堵最大的子树来个特判。如果老鼠钻到最大的子树都问题不大的话，就不必堵最大的子树了。

细节较多。

星座3

给一张 $n \times n$ 的由建筑物（白），夜空（黑）和星星（黄）三种像素组成的照片。建筑物占第 $i$ 列的下面 $a_i$ 行，星星有 $m$ 个，第 $i$ 个坐标为 $(x_i,y_i)$，权值为 $v_i$。其余全为夜空。

我们称对于原照片的一个子矩形，如果以下两个条件成立，则被称作一个星座:

矩形区域中没有白色像素。

矩形区域中有两个或多个黄色像素。

现要求移除一些星星（黄变黑），使得不存在星座。保留第 $i$ 个星星的收益为 $v_i$，求最大收益。

$1 \le n,m,x_i,y_i,a_i \le 2 \times 10^5,0 \le v_i \le 10^9$

有一个显然的图论模型，互相冲突的星星之间连边，然后求一般图最大带权独立集。然而是个 NP Hard 问题...

比较奇怪？不知从何下手？那么快想贪心DP网络流！

DP网络流复杂度较高，并且不好找子结构，还不是二分图。于是只剩贪心。

我们从下向上考虑星星。如果有星星既靠上（容易冲突）又收益小，那么肯定不要它。否则的话，我们或许可以留下它；但是可能会和以后的某些价值很大的星星冲突，所以需要用类似反悔的思想，在它以后可能和其它星星冲突的地方（控制区间）记一个"代价"。以后的星星遇到这种冲突的时候，如果自己的价值足够大（比代价大），那么就将"价值-代价"计入答案，表示选上这个，放弃那个冲突的星星；然后再在以后可能和它冲突的地方留个代价为"价值-代价"。

注意不要删除之前的那个代价，因为如果以后同时和这个星星以及之前那个星星冲突的话，我们需要减去当前代价，放弃当前这个星星，恢复原来那个星星，然后再放弃原来的星星，恢复原来的原来的星星......一直到不冲突为止。由于如果更高的星星和较低的星星冲突的话，它们的“控制区间”应该是包含关系，因此不会出现把之前的代价算上而不算当前代价的情况。

[HAOI2017]字符串

给一个大串 $S$ 和一堆小串 $p$，对于每个小串，求出其在 $S$ 中的出现次数。

这里的判断字符串相同的方法有所不同。两串相同，当且仅当 $|s|=|t|$ 并且 $|lcp| + |lcs| + k \ge |s|$，其中 $k$ 为给定的一常数。特别地，如果 $|s| = |t|,|s| \le k$，那么我们认为 $s = t$。

$1 \le |S|, \sum|p| \le 2 \times 10^5$

首先多串匹配问题需要想 AC自动机。如果用 SAM 一个一个地整的话，可能能撑过 $|lcs|$，但是再来个 $|lcp|$ 就没办法了。于是我们考虑统一对小串 $p$ 计算答案。

对于一个小串 $p$，我们可以枚举其跟 $S$ 的 $cp$ （公共前缀），然后再要求第 $cp + k + 1...|p|$ 都一样，就一定是合法串了。那么我们现在有俩限制，形如：$|cp| = t_1,|lcs| \ge t_2$。我们可以在 AC自动机上枚举 $cp$ 的那个点，然后找到其反串中$|p|...|cp|+k+1$ 所在的点。统计大串至少有 $cp$ 这个串（可以任意向前加字符），并且在那个 $cp$ 向后隔 $k$ 个字符后又至少又出现了 $cs$ 串（可以任意向后加字符）。这个可以通过当前大串的某些前缀在$fail$ 树中 $cp$ 的子树中，其向后 $k+1$ 个字符后的那个位置对应的反串“前缀”的对应节点在小串的 $|p|...|cp|+k+1$ 位置对应的反串的对应节点的子树中。

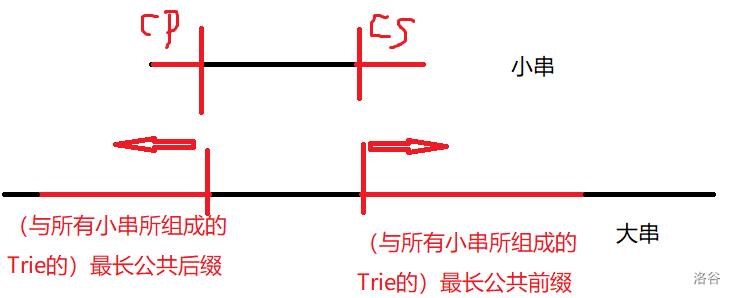
具体来说，我们可以对所有小串都进行以下操作：

将正反串均加入到 Trie 中。
对于每个正串前缀节点 $p$，找出其对应的（位置 $+k+1$）反串“前缀”节点 $q$，将 $q$ 记录到 $p$ 上。

然后建出 AC自动机，再对大串进行以下操作：

对于每个前缀前缀跑出的节点 $p$，找出其对应的（位置 $+k+1$）反串“前缀”节点 $q$，将 $q$ 记录到 $p$ 上。

然后DFS Fail 树，在DFS的过程中，对于大串的操作是：

遍历到现节点 $p$ 时，在其所有对应节点 $q$ 上打一个标记。

对于小串的操作是：

遍历到现节点 $p$ 之前记录其对应节点 $q$ 子树内的标记和。
对大串操作并进入 $p$ 的子树中。
回溯前再次查询其对应节点 $q$ 子树内的标记和，利用两次之差确定有多少标记，记到对应小串的答案上。

最后，每个小串都有其对应的答案了，即为 $f(k)$。

如果这是个最优化问题，那么我们已经做完了，因为我们统计到了所有合法匹配的信息。然而我们计重了，对于真正的 $|s|-|lcp|-|lcs|=t$ 的情况，我们计算了 $k-t+1$ 次。其中中间（我们认为的）不同的部分为 $|s|-|lcs|-k...|s|-|lcs|+1$ 和 $|s|-|lcs|-k+1...|s|-|lcs|+2$ 一直到 $|lcp|+1...|lcp|+k$ 都会将同一种情况统计一遍，所以计算了 $k-t+1$ 次。形式化地，记我们计算的答案（不同部分最多长为 $k$的方案数）为 $f(k)$，记真正的不同的部分长度恰好为 $k$ 的情况的方案数为 $g(k)$，那么有关系式：

\[f(k)=\sum_{t \le k}(k-t+1)g(t) \]

不能用二项式反演，但是发现系数是等差数列，可以用类似树上的僵尸的处理办法解决。即：

\[Answer=f(k)-f(k-1) \]

错位相减后发现正好得到了我们想要的答案：$\sum_{t \le k}g(t)$。

然后发现只有10pts。因为这种算法会在一些边界情况下算错。

但是我们发现所有不合法情况都是 $f(k-1)$ 的一边到达了 $0/len$，于是我们可以强制让 $f(k-1)$ 不能边界为 $0/len$，即不能顶着两边，然后 $f(k)$ 和 $f(k-1)$ 少算的情况数就相同

Buy One, Get One Free

现需要买 $n$ 个物品，第 $i$ 个物品的价格为 $v_i$，买一个物品可以赠送一个价格严格小于它的物品，这个物品由我们决定。求最小费用。 $n \le 5 \times 10^5, 1 \le v_i \le 10^9$

贪心。

首先题目可以转化为最大化免费物品的价值总和。显然可能有两种操作：直接买，（如果之前有买过的话）用之前买的使当前免费。

如果物品价格互不相同的话，直接从大到小依次决策即可。可惜现在有可能相同，然后就可能需要撤销之前的“被赠”的操作，腾出来两个被买的来使得当前这两个相同的被赠，获得 $2w-k$ 的收益。然而这种撤销是不稳定的，如果后面还有比较贵的物品，我们就可能要还原回去，把当前这两个相同的都买上，使得后面俩“较贵”的物品被赠，实现“买一赠二”的效果。当然如果“较贵”的物品没俩，只要有大于 $2w-k$ 的物品，我们就可以通过一波调整使得收益为 $v$ 并且还有一个多的买的物品。

具体实现用堆来处理。注意一下不能出现买价值 $v$ 赠价值 $v$ 的现象。

[CTS2019]重复

给定一个长为 $n$ 的由小写字母构成的字符串 $S$ ，求有多少长为 $m$ 的由小写字母构成的字符串 $T$，使得无穷个 $T$ 依次接到一起后存在一个长为 $n$ 的字典序比 $S$ 小的子串。$1 \le n,m \le 2000$

做这题怎么有点 surreal 的感觉？

首先一步容斥，问题转化为不存在比 $S$ 小的子串。这样是不是有点类似病毒的意思？不过这题要比那个题难好多。我们建出 $S$ 的 AC自动机，假设我们得到了无穷个 $T$ 拼起来的串，那么我们要求只能跳 $p$ 及其 fail 树的祖先的出边的最大值的那个字符，否则就会出现比 $S$ 字典序小的子串了。这样的话，我们就可以把 AC自动机删得只剩下合法边，发现对于 $p$ 的出边，只可能是那个最大字符所对应的边的点，或者是 $0$。

然而我们并不能搞到无穷个 $T$ 拼起来的串，也不知道该怎么计数。然而发现跑了足够多的 $T$ 以后，再跑一个 $T$，AC自动机上的节点不会改变。并且，如果我们知道在 AC自动机上，从 $p$ 开始，跑 $m$ 步，如果又回到了 $p$，那么一定对应着唯一的合法的 $T$（我们能够构造出来唯一的合法解）。于是我们能够将问题转化为从 $p$ 开始走 $m$ 步又回到 $p$ 的方案数。

显然有一个显然的 $O(n^3)$ 做法:$f(s)(k)(p)$ 表示从 $s$ 出发，走 $k$ 步，到 $p$ 的方案数。答案为 $\sum f(s)(m)(s)$。

然而发现我们在 AC 自动机上的边只有两种边，并且其中一种为到 $0$ 的边。于是我们可以预处理出从 $0$ 开始走 $k$ 步到 $p$ 的方案数，这样就可以优化到 $O(n^2)$ 了。

Balance Beam P

有一序列，每个位置有权值 $w_i$。一开始人的初始位置为 $s$，每次可以选择获得当前位置权值的收益并结束，或者等概率向两边走。走到 $0$ 或者 $n+1$ 则被迫结束并不获得收益。对于每个 $1 \le i \le n$，求 $s=i$ 时的最优决策下的期望收益。 $2 \le n \le 10^5$。

设 $f(i)$ 表示当前在 $i$ 位置，最优决策下的期望收益。那么显然有：

\[f_i = \max(w_i,\frac{1}{2}(f_{i+1}+f_{i-1})) \]

显然当 $w_i$ 为全局最大的时候 $f_i = w_i$。$f_i$ 不是全局最大，但是左右都不是很优秀的时候也有 $f_i = w_i$。而对于其余的 $i$，都有 $f_i = \frac{1}{2}(f_{i+1}+f_{i-1})$，即 $f_i$ 为两边的均值。那么如果有一段都满足 $f_i = \frac{1}{2}(f_{i+1}+f_{i-1})$ 的时候，$(i,f_i)$ 就在平面上形成了一条线段。因此 $(i,f_i)$ 在平面上应该表现为一条折线。又因为 $f_i \ge \frac{1}{2}(f_{i+1}+f_{i-1})$，所以不会出现下凸的情况，因此 $(i,f_i)$ 在平面上应该表现为一个凸包，并且顶点为 $(i,w_i)$。又因为 $f_i \ge w_i$，所以 $(i,f_i)$ 应该与 $(i,w_i)$ 形成的凸包相同。因此直接建出 $(i,w_i)$ 的凸包，对于每个 $i$ 求其在凸包上的点的纵坐标即可。

New Year and Boolean Bridges

我们要构造出一个有向图。

设 $f(i,j)$ 表示 $i$ 是否能直接或间接到达 $j$。

给定一 $n \times n$ 的运算符号矩阵 $G$，仅包含 $\and,\or,\oplus$（与，或，异或）。若 $G_{i,j} = op$，则要求 $f(i,j) ~ op ~ f(j,i) = 1$。

求该有向图的最少边数是多少。无解输出 $-1$。

$n \le 47$

显然“与”即可缩为一个SCC，其余可以串成一个链，这样的话正确性是没有问题的（然后我就交了一发发现WA on 5）。

显然这并不是最优的，因为如果我们能够将两个SCC合并的话，就会省掉一条边。

现考虑合并SCC。发现如果两SCC没有异或关系，就可以合并。于是问题转化为了将各SCC用异或关系连边，需要将它们分成尽可能少的独立集。（然后开始想模拟退火...）

发现对于大小为 $1$ 的SCC，它们合并与否对答案贡献都是 $1$，因此可以扔掉，这样最多剩下 $23$ 个SCC。于是就可以想一些指数级复杂度的算法了。

可以从小到大枚举 $k$ 表示最少能分成 $k$ 个独立集，设 $f(s)$ 表示 $s$ 这个集合是否是独立集，那么能分成 $k$ 个独立集就相当于对 $f(s)$ 做子集卷积求出 $f^k$，$f^k(U) \not = 0$，其中 $U$ 是全集。复杂度：$O(n^32^n)$。

发现复杂度有点危险，但是似乎不用做子集卷积，或卷积即可。于是复杂度降为 $O(n^22^n)$。

又发现每次只是求 $f^k(U)$，于是不用FWT来FWT去，只需要每次在高维前缀和的状态下乘，单点查 $f(U)$ 的值即可。因为 $f(U) = \sum_{S \in U}g(S)$，所以子集反演 $g(U) = \sum_{S \in U}(-1)^{|T|-|S|}f(S)$。复杂度降为 $O(n2^n)$，就可以稳过了。

萌萌哒

现有一 $n$ 个点的无向图，有 $m$ 条以下形式的信息表述：

给定 $l_1,r_1,l_2,r_2$，保证 $r_1 - l_1 = r_2 - l_2$，表示对于 $i \in [0,r_1-l_1)$，$l_i + i$ 与 $l_2 + i$ 之间有无向边。

问连通块个数。

$n,m \le 10^5,1 \le l \le r \le n$

sto zzz orz，zzz一年前就会了，我现在还是想不出来qaq

显然需要并查集。不知道怎么回事我们想到了ST表，可以把每个操作拆成两个长度为 $2$ 的整次幂的操作。对于每个 $j$，将所有长度为 $2^j$ 的操作进行合并。然后很重要的一点：长度为 $2^j$ 的区间在某个块里，完全等价于那个区间拆成的两个长度为 $2^{j-1}$ 的区间分别在那个块所拆成的两个块里。于是可以将大区间推到小区间里。然后这题就做完了。复杂度：$O(nlog^2n)$

[POI2012]WYR

给定$n$个数和$a,b$每次可以选择一段区间$+a,-a,+b$或$-b$，问最少操作几次能把他们都变成 $0$

$ n \le 10^5$

显然无解可以通过是否整除 gcd 来判断，于是问题转化为了 $a,b$ 互质的问题。

根据套路，区间加减转化为差分数组上的单点加减。对于每个点，设其加/减 $a$ 的次数为 $x$（加正减负），加/减 $b$ 的次数为 $y$。那么有 $ax_i+by_i=h_i$。如果只考虑单点对答案的贡献 $|x_i|+|y_i|$，其关于 $x$ 是一个单峰函数，且在 $x_i=0$ 附近或 $y_i = 0$ 附近取到极值。函数的样子大概是：从 $x_i = -\infty,y_i = \infty$ 开始，先猛烈下降，然后当 $x_i$ 变为正的时候开始缓慢下降或者缓慢上升（取决于 $a,b$ 的大小关系），然后当 $y_i$ 变为负数的时候开始猛烈上升。

我们可以先 exgcd 来取到局部最优解，然后再逐渐调整到全局正确且最优解。因为代价函数是单峰函数，所以可以堆贪心，就类似pancake的做法做就好了。

论战捆竹竿

给定一个长为 $n$ 的字符串，问使用所有 $n-|T|$ 的数通过相加和数乘的方式能到达的小于等于 $W$ 的数的个数。其中 $T$ 为 $S$ 的一个 border 或者是空串。其中 $A$ 是 $B$ 的 border 当且仅当 $|A|<|B|$ 并且 $A$ 既是 $B$ 的前缀又是 $B$ 的后缀。

$n \le 5 \times 10^5,W < 10^{18}$

显然有一个类似寻梦的套路的做法：搞出所有数，使用最小的那个最为模数，跑同余最短路。然而边数达到了 $(n-maxborder) \times bordercnt$，可能会达到 $n^2$ 的级别，无法通过。但是，根据border的性质，这些数可以被划分为 $O(\log n)$ 个等差数列，我们可以单独对每个等差数列考虑然后合并。

对于等差数列 $b,b+d,b+2d,...,b+ld$，其在模 $b$ 的意义下类似于多重背包，只不过上限并不是 $\lfloor \frac{n}{v}\rfloor \times v$，而是呈环状转移。但是环上的最小点是不会被更新的（这又是一个经典套路），我们以那个点作为起点跑单调队列即可。注意，这里的最短路数组 $dis_u$ 表示的是余数为 $u$ 的最小的能到达的数。

现在考虑合并两个等差数列，或者说将模 $b$ 意义下的最短路数组转换为模 $b'$ 意义下的。首先可以直接根据 $dis$ 的值转移，但是原来还可以随意加 $b$ 来转移，这体现在新数组中相当于有一个无限长的等差数列$b,2b,3b,...$。类似上面的方法再搞搞就好了。不过这次不是多重背包就不用单调队列了，直接记最小值即可。

细节较多。

ZS Shuffles Cards

有 $n$ 张标号为 $1...n$ 的牌和 $m$ 张鬼牌。初始时有一空集合 $S$。现在我们打乱这些牌，然后开始抽牌游戏，每一轮你可以抽一张牌：

如果抽到了牌 $x$，那么移除该牌并将 $x$ 加入集合 $S$。

若抽到了鬼牌，那么将移除的牌重新加入牌堆并打乱，但不清空 $S$。

如果抽到鬼牌并且当前 $S$ 包含了 $1...n$，那么游戏结束。

求游戏结束期望进行时间。

$1 \le n,m \le 2 \times 10^6$

即使 $S$ 包含了 $1...n$，但是没抽到鬼牌，那么游戏也仍然无法结束。所以可以将“抽到鬼牌”看作一步，问题转化为游戏结束期望要抽几次鬼牌。这个可以用min-max容斥做，但是有更简单的做法：

设 $f_i$ 表示还差 $i$ 张牌，到结束的期望抽鬼牌次数。那么既然状态定义的是抽鬼牌的期望次数，并且 $i$ 以外的牌都已经在集合中了，那么我们就可以一抽到 $i$ 以外的牌就扔掉，即忽略掉 $i$ 以外的牌。那么可以根据下一次抽到的是不是鬼牌分两种情况考虑转移：

\[f_i=\frac{m}{m+i}(f_i+1)+\frac{i}{m+i}f_{i-1}\\ f_i = f_{i-1}+\frac{m}{i}\\ f_0 = 1 \]

递推可得 $f_n$。

现在我们还有一个问题：抽到鬼牌期望要多少次。可以考虑其余数的影响，如果一个数出现在了第一个鬼牌之前，那么就会有 $1$ 的贡献。而一个数有 $\frac{1}{m+1}$ 的概率出现在第一个鬼牌之前。因此抽到鬼牌期望要 $1 + n \times \frac{1}{m+1}$。

最终答案为 $f_n \times (\frac{n}{m+1}+1)$。复杂度 $O(n)$

count

我们定义一个序列为合法序列当且仅当其长度为 $n$，包含了 $1...m$ 的所有数至少一遍。

对于一个序列 $A$，定义 $f_A(l,r)$ 表示 $l...r$ 中最大值所在下标（多个下标的话取最小）。定义两个合法序列本质相同，当且仅当对于任意的 $l,r$，都有 $f_A(l,r)=f_B(l,r)$。

现给定 $n,m$，求本质不同的合法序列数。

subtask1 : $m \le n \le 10^5$。

subtask2 : $m \le n \le 10^7$

观察 $f_A(l,r)$ 表示最大值的位置，强者或许能想到笛卡尔树（左儿子严格小于爹，右儿子小于等于爹）。根据 $f_A(l,r)$ 数组，我们就可以建出唯一的笛卡尔树；根据已知的笛卡尔树，我们也可以求出唯一的 $f_A(l,r)$ 数组。因此本质不同的序列数转化为求合法的笛卡尔树数。

如果没有 $m$ 的限制，那么任意的笛卡尔树均是合法的，答案为一卡特兰数。

现在考虑 $m$ 的限制，那么就相当于要求所有节点向左延伸（含自己）不超过 $m$ 个节点。于是我们可以设此状态为 $f(n,m)$，枚举左右儿子的节点数可以得到递推式：

\[f(n,m) = [n=0] + \sum_{k \le n}f(k,m-1)f(n-k-1,m) \]

然后我们就可以 $O(n^2m)$ 地求了。

然而还是不够快。发现右边是个卷积，模数还很友好，于是可以上分治 NTT 或类似多项式求逆之类的科技，做到 $O(nm \log n)$。

然而还是不够快。我们可以继续推一波式子：设 $F_m(x) = \sum_{i \ge 0}f(i,m)\times x^i$，然后：

\[F_m(x) = xF_{m-1}(x)F_m(x) + 1\\ F_m(x) = \frac{1}{1-xF_{m-1}(x)} \]

这个就是上面说的求逆。然后我们可以设 $F_m(x) = \dfrac{A_m(x)}{B_m(x)}$，然后化简得：

\[\begin{aligned} \frac{A_m}{B_m} &= \frac{1}{1-x\frac{A_{m-1}}{B_{m-1}}}\\ &= \frac{B_{m-1}}{B_{m-1}-xA_{m-1}} \end{aligned} \]

（也不知道怎么想出来的）

初始的 $A_0,B_0$ 可以随便搞一下。然后递推的话可以构造一下，让 $A_m = B_{m-1},B_m = B_{m-1}-xA_{m-1}$。发现这个是线性递推，可以用矩阵快速幂搞。复杂度：$O(n\log n\log m)$

注意到可以认为最终多项式次数小于等于 $n$，于是可以直接把点值带进去搞搞，最后多项式快速插值，就不用在快速幂里面搞NTT了。复杂度：$O(n\log^2 n)$。

然而不是很可写。有一个小技巧：插值的时候直接带进去单位根，这样就可以直接 IDFT 了。

最终整出来 $A_m,B_m$ 之后需要多项式求逆。

发现这是多项式的极限了，毕竟多项式一个乘法就要 $O(n\log n)$。现在考虑回到多项式之前，尝试从卡特兰数那里搞些事情。

由于卡特兰数既可以搞二叉树，又可以搞括号序列，还可以搞网格图路径计数问题。既然括号序列能转化为网格图路径计数问题，那么我们尝试用较为直观的方式将二叉树计数转化为括号序列问题和网格图问题。

对于一个二叉树，我们从根开始DFS。当DFS到一个点的时候，加入一个左括号；当从左儿子回来的时候，加入一个右括号；当从右儿子回来的时候，不加括号。这样，我们得到一个括号序列。较为显然的是，这个括号序列和二叉树是一一对应的。并且一个有意思的性质是，当我们将此问题看作进栈出栈问题的时候，当前的左括号数即为当前点的左链长。因此，$m$ 的限制转化为了任意位置之前的左括号数减右括号数不超过 $m$。

现在我们可以大摇大摆地在网格图上计数。我们现在有两个限制：不能到达 $y=x-1$ 和 $y=x-m-1$ 这两条线。要求从 $(0,0)$ 走到 $(n,n)$ 的方案数。考虑总方案减去不合法方案。如果一段时间内仅碰到过第一条线，我们用 A 来表示；如果仅碰到过第二条线，用 B 来表示。那么一个不合法序列可以由 ABABABA 之类的东西来表示。现在我们将 $(n,n)$ 关于 $y=x-1$ 对称到点 $(x',y')$，所算的方案数是含有 A 的序列数，记为 $g_1$；然后我们再将 $(x',y')$ 关于 $y=x-m-1$ 对称到点 $(x'',y'')$，所算的方案数是含有 ...B...A... 的序列数（反过来想，先碰到第二根线，然后对称回来走，碰到第一根线，再对称回来走，到达 $(n,n)$），记为 $g_2$...然后我们再对先对称第二条线的情况再算一遍，记为 $h_1,h_2,...$。显然，对称到一定次数以后就超出界限了，以后的方案数均为0，可以停止。最终答案为 $\sum_{i > 0}(g_i+h_i) \times (-1)^{i}$。

证明考虑对 ABABA 的贡献，A处会减一，BA处会加一，ABA处会减一...ABABA处会减一，于是第一遍对其的影响为 -1；B处会减一，AB处会加一，BAB处会减一，ABAB处会加一，于是第二遍的影响为0.发现对于任意的AB序列，两边中总是恰好有一遍是 -1，一遍为0.于是总贡献为-1，是正确的。

复杂度：$O(n)$。代码非常短。

Shifting Dominoes

有一个 $n\times m$ 的棋盘，被 $1 \times 2$ 的骨牌覆盖，保证 $2 | n \times m$。

现在你需要执行以下操作：

移去恰好一个骨牌。

将其他骨牌沿着其长边进行移动。

你需要保证每张骨牌的最终位置与初始位置至少有一个交点。

求你通过若干次操作后可以得到的所有可能的局面的数量。

两种局面不同，当且仅当在其中一者中某个位置被骨牌覆盖，而另一者没有。

$ n \times m \le 10^5$

考虑一个空格的移动路线。如果 $(x,y)$ 旁边有骨牌 $(x+1,y),(x+2,y)$，那么这个空格的移动路线为 $(x,y) \to (x+2,y)$。我们可以将类似的移动路线看作边建出来，发现是一些森林。现在证明这是一些森林。

每个点只有至多一个入度（如果骨牌靠着边界，那么可能入度为0）。
无环。如果有环，那么我们可以将路线（或者可以理解为骨牌）围成的那个多边形的边界伸成一个长方形，发现其长和宽均为奇数，因此里面的区域只有奇数个格子，而一个骨牌占俩位置，因此不存在合法状态。

并且这个森林还有一个奇妙的性质：对网格图黑白染色后，每棵树内的点的颜色全部相同（显然）

如果钦定一开始移去骨牌$(x,y),(x',y')$，那么会产生两个空格，而这两个就可以在各自的子树内随意游走，因此局面数为子树大小的乘积。

现在同时考虑移去每个骨牌的情况，发现有些局面会算重。但是，如果我们把局面放到二维平面上，横坐标为白点的森林的dfn，纵坐标为黑点的dfn，那么一个骨牌能到达的局面是一个矩形，所有骨牌能到达的局面就是这些矩形的并。于是扫描线随便搞搞就好。

最小乘积生成树

给定 $n$ 个点 $m$ 条边的无向图，边有两种边权 $a_i,b_i$。求最小乘积生成树，即最小化：

\[\sum_{i}a_i \times \sum_{i}b_i \]
$n \le 200,m \le 10000,0 \le a_i,b_i \le 255$

根本想不到啊qaq

设 $x = \sum_ia_i, y = \sum_i b_i$，可以将每个生成树看作二维平面上的点，那么最小乘积生成树一定在左下凸壳上。

先求出关于 $x$ 的最小生成树，在平面上表示为点 $A$；求出关于 $y$ 的最小生成树，在平面上表示为点 $B$。那么 $A,B$ 分别是最左和最下的点，可以用来更新答案。

现在要求凸包内剩余的点。我们可以先求出距离 $AB$ 最远的点 $C$，然后分治做。

考虑如何计算点 $C$。距离 $AB$ 最远即最大化 $S_{\triangle ABC}$，这个可以用叉积来判断，于是转化为最小化 $\vec{AB} \times \vec{AC}$。推式子化简得需要最小化 $(y_a - y_b) \cdot x_c + (x_b - x_a) \cdot y_c$。那么我们可以以 $(y_a - y_b) \cdot a + (x_b - x_a) \cdot b$ 为依据求最小生成树，那棵最小生成树即为点 $C$。

当发现找不到点 $C$ 的时候返回即可。

复杂度比较玄学。因为最小生成树边权和较小，横纵坐标不超过 $25500$，因此凸包上最多有 $50000$ 左右的点。根据 lsr 所说，据EI说凸包上的点数最大是 $(nw)^{\frac{2}{3}}$，所以总复杂度为 $O(n^{\frac{8}{3}}w^{\frac{2}{3}})$。Kruskal为 $O(m \log m (nw)^{\frac{2}{3}})$。

圆上的整点

求圆：$x^2+y^2=r^2$ 上的整点个数。

$r \le 2 \times 10^9$

根本怎么想出来的/kk

\[x^2+y^2=r^2\\ y^2=(r+x)(r-x)\\ \]

故 $(r+x)(r-x)$ 为完全平方数。

设 $d = \gcd(r+x,r-x)$，那么 $\frac{r+x}d,\frac{r-x}d$ 一定是互质的完全平方数。

现考虑 $d$：

\[d=\gcd(r+x,r-x)\\ d=\gcd(r+x,2r) \]

故 $d$ 只可能是 $2r$ 的约数。可以枚举。

由于 $\frac{r-x}d$ 为完全平方数，且不超过 $\frac{r}{d}$，数量较少，可以枚举。

两个都枚举好后，就可以知道 $x$ 了，就可以推 $y$ 了。

复杂度：$O(\sigma_0(r)\sqrt r \log r)$，严重跑不满。

组合数问题

给定 $n,k,r,P$，求：

\[\left( \sum_{i = 0}^\infty \mathrm{C}_{nk}^{ik + r} \right) \bmod P \]
$n \le 10^9,0 < r < k \le 50,P < 2^{30}$。不保证 $P$ 是质数。

又是组合数问题...

然而这回既不是杨辉三角，也不是斯特林数。~~看起来有点像单位根反演~~

那个 $n$ 实在太大，我们的复杂度不能和 $n$ 有关系，或者只能是 $\log n$ 或 $\sqrt n$。看到 $r,k$ 的范围能想到什么呢？~~折半搜！~~矩阵快速幂！

然而一切都没用，我们还是不知道怎么做。在尝试上指标求和平行求和法吸收恒等式范德蒙德卷积等无果后，~~就自闭了~~只能尝试一下组合意义。

其实这个式子的组合意义很简单，就是 $nk$ 个球中选择 $r (\bmod k)$ 个球的方案数。那么我们可以设 $f(i,j)$ 为答案，那么有：

\[f(i,j)=f(i-1,j)+f(i-1,(j-1) \bmod k) \]

最终答案为 $f(nk,r)$。

运用矩乘优化，复杂度 $O(k^3\log n)$。

似乎还有生成函数做法，可以做到 $O(k^2 \log n)$，但是那个就比较神仙了。

取石子游戏

$n$ 堆石子的 nim 游戏，但是每次每个人只能取最左边或最右边的那堆的石子。给定每堆石子的数量 $a_i$，问是否先手必胜。多组数据。 $T \le 10,n \le 1000,a_i \le 10^9$。

首先，由于找不出规律，我们基本上可以放弃 SG 函数了。

考虑区间DP。设 $f(l,r)$ 表示区间 $l,r$ 再在左边加上一堆 $f(l,r)$ 的石子就会先手必败；$g(l,r)$ 表示区间 $l,r$ 再在右边加上一堆 $g(l,r)$ 的石子就会先手必败（这种状态好像是套路?第一次看到)。显然$f(l,r),g(l,r)$ 是唯一的。并且 $f(i,i)=g(i,i) = a_i$（这个就是正常的 nim 游戏）。现在考虑递推：

仅考虑 $f/g(l,r-1) \to f(l,r)$ 的情况。$f/g(l+1,r) \to g(l,r)$ 也类似。可以考虑构造先手必败的情况。

当 $a_r < \min (f,g)$ 的时候，我们可以在左边构造出一堆 $a_r$ 的石子，先手拿多少，后手拿多少，最后肯定有先手全拿完的情况，此时后手没拿完；而后手仅在 $now_r=g$ 的时候会必败，此时不会，因此先手必败。
当 $a_r = g$ 的时候，显然可以在左边构造出 $0$。
当 $f \le a_r < g$ 的时候，如果再用第一种策略，先手可能会直接将 $a_r$ 砍成 $f$，如果后手跟着把左边砍成 $f$，那么后手就输了。因此应该略微改变策略，让左边保持在 $f$ 的上面。根据手玩得出，左边放 $a_r+1$ 先手必败。
当 $g < a_r \le f$ 的时候，与上一种情况类似，我们需要保持右边始终比左边大 $1$，即左边放 $a_r - 1$。
当 $a_r > \max(f,g)$ 的时候，可以构造出左边放 $a_r$ 这么多，这样的话后手可以根据先手的策略，在前几种情况中找到一种自己必胜的策略。

最终根据 $f(2,n)$ 是否和 $a_1$ 相等来判断是否先手必胜。

复杂度：$O(Tn^2)$。

Uniformly Branched Trees

给定 $n$ 和 $d$，求有多少个 $n$ 个点的不同构的树，满足所有节点的度数不是 $1$ 就是 $d$。

这里给出不同构的定义：树 $A$ 和树 $B$ 不同构，当且仅当不存在一种编号到编号的映射关系 $p_i$，使得 $A$ 中的边 $(u_i,v_i)$ 对应 $B$ 中的边 $(p_{u_i},p_{v_i})$。

$1 \le n \le 1000, 2 \le d \le 10$

题意中要求的是无标号无根树计数，prufer序列是用来搞有标号无根树的，不好使。因此我们需要再找其它方法。

无根树实在太难搞了，我们需要将其转化为有根树。为了不重不漏地计数，我们需要找到无根树的独一无二的点：重心（至少在奇数个点的树中是这样的）。

设 $f(i,j,k)$ 表示 $i$ 个点的树，有 $j$ 个子树，子树大小不超过 $k$ 的方案数。这样的话最终答案（假设只有一个重心）为 $f(n,d,n/2)$。

考虑转移。考虑子树中最大的大小是否为 $k$，如果比 $k$ 小，那么方案为 $f(i,j,k-1)$；如果为 $k$，可以枚举有几棵子树的大小为 $k$。设有 $t$ 棵子树的大小为 $k$，那么剩余的方案数应该是 $f(i-tk,j-t,k-1)$，现在考虑 $t$ 棵子树大小均为 $k$ 的方案数。

发现这实质上是“$n$ 种球，每种球有无限个（可重复），在其中拿 $k$ 个的方案数”。如果不让重复拿一种球，那就太水了，直接组合数即可。但是我们可以给拿过的球一些重复拿的机会。现在这里给出一种做法：

在 $n$ 个球后面再放 $k-1$ 个特殊球，从总共的 $n+k-1$ 个中拿出 $k$ 个的方案数即为所求。即，方案数为 ${n+k-1 \choose k}$。

现在给出证明：

拿普通球表示选那个球一次；拿第 $i$ 个特殊球表示（所有拿出来的球中）第 $i+1$ 个球和第 $i$ 个球相同。因此一种情况唯一对应一种合法方案。
对于一种合法方案，显然也唯一对应我们这里的一种情况。

2020.10.29 Update:

从Alansp那里学到了一种更好的理解方式：

考虑插板。这个问题可以转化为将 $k$ 个无标号球涂成 $n$ 种颜色，每个球必须涂色，每种颜色不一定需要被涂，的方案数。那么就又可以转化为了 $k$ 个球分成 $n$ 个集合，集合可空，的方案数。这时可以直接用插板法解决，方案数为 ${k + n - 1 \choose n - 1}$。

现在我们得到了完整的DP式子：

\[f(n,i,1)=1;f(1,0,i)=1;\\ f(i,j,k) = f(i,j,k-1) + \sum_{t \ge 1} f(i-tk,j-t,k-1) \times {f(k,d-1,k)+t-1 \choose t}\ \]

如果这棵树的点数为奇数，我们这样做没有问题。如果为偶数，我们可能会多算一些东西。不过当这棵树点数为偶数，并且有两个重心的时候，这两个重心见一定有一条边直接相连，且这条边两边的树的大小一样。如果这两棵树的方案相同，我们不会计重（可以考虑找到我们假设一个重心时最大的那棵大小为 $n/2$ 的子树，那个子树完全相同，且外面情况完全相同，因此单重心的时候不会计算两次）；如果这两棵树的方案不同，那么我们会计重。于是我们需要减去两棵树中不同的方案对数，即 ${f(n/2,d-1,n/2) \choose 2}$。

那么最终完整的答案应该为：

\[Ans = f(n,d,\lfloor \frac{n}2 \rfloor) - [2 | n] {f(n/2,d-1,n/2) \choose 2} \]

还有个小细节：这题多次用到 $n$ 巨大 $m$ 巨小的组合数 ${n \choose m}$。这个是可以拆开算的：$\dfrac{(n-m+1)...n}{m!}$。然后发现这里 $n$ 是可以取模的，因此我们就可以放心大胆地对 $f$ 进行取模了。

复杂度：$O(n^2d^2)$（组合数暴力求的话是 $O(n^2d^3)$ 的）。但是实际上合法的方案数并不多，记搜或许会更快些。然而我写了个刷表法被卡了qaq（尽管后来发现是求组合数的时候没有判 m > n 的情况导致出现一些玄学问题）

总之这题还是挺神的，需要用到好多计数技巧，还需要严谨的思维来判断是否算多是否少算。熟练掌握计数方法的人可能会觉得这题难度一般，但是对于我来说还是很难的，觉得不止有 $2700$ 。或许对于zzz和lsr来说根本没 $2500$ 吧。

Mergesort Strikes Back

一个长度为 $n$ 的随机排列，进行深度为 $k$ 的归并排序，求期望逆序对个数。答案对一个素数取模。

$1 \le n, k \le 10^5,10^8 \le P \le 10^9$

首先需要搞几个性质:

叶节点中的数对的位置关系不变

（显然）

因此一个叶节点内的数对的贡献就都是 $1/2$ 了。

对于叶节点搞出一个单调栈（单调递增），那么单调栈中的每个点所代表的块（含最大值和一些小跟班）在整个排序过程中都是挨在一起的，可以一块考虑。

因为较小的那个最大值取出后，小跟班也会跟着出来。

归并的时候都是以单调栈的形式。

然后考虑叶节点之间的贡献。对于 $A$ 节点的 $i$ 和 $B$ 节点的 $j$ 个来说，如果他们都不是 $1...i$ 并 $1...j$ 的最大值的话，那么他们的贡献为 $1/2$，这个可以通过大力分类讨论得出；如果其中有一个是这 $i+j$ 个数中的最大值的话，那么那个较大数一定会被带到后面（其它情况的话总是有一个会被带到后面，而到底是 $A$ 的那个还是 $B$ 的那个是等概率的）于是这种情况的贡献为 $0$。因此叶节点间的 $(i,j)$ 的贡献为都不是最大值的贡献，即 $\frac{1}2 \times \frac{i+j-2}{i+j} = \frac{1}2 - \frac1{i+j}$。于是总贡献为 $\sum_{i = 1}^{|A|} \sum_{j = 1}^{|B|} \frac{1}{2} - \frac{1}{i+j}$，这个随便搞搞就好。

还有一点要说的是，相邻较远的叶节点间的贡献不会收到之前归并的影响，因为如果归并过来小节点并不会对 $i,j$ 是否是两前缀的最大值产生影响；归并过来大节点的情况是不存在的，因为归并的时候都是以单调栈的形式。

楼房重建

有一长为 $n + 1$ 的序列 $a_i$，从 $0$ 开始编号，初始值均为 $0$。

现有 $m$ 种操作，每次修改 $a_i$。

每次操作后，问单调（严格）递增的单调栈长度。（例如 $1,2,2,3,1,1,1,1,5$ 的单调栈长度为 $4$）

$1 \le n,m \le 10^5,1 \le a_i \le 10^9,1 \le i \le n$

可以用数据结构维护。这里用线段树维护单调栈长度。

肯定要维护个 $v_x$ 表示单调栈长度，但是仅此还不够，我们看看线段树合并俩节点需要做些啥。

假设我们已经知道了两个儿子节点的单调栈长度，那么左儿子的单调栈一定还保留着，而右儿子的单调栈需要被截去小于等于左儿子的最大值的那部分。因此我们肯定还需要维护节点的最大值 $mx$。现在考虑如何搞出右儿子里大于左儿子最大值 $mx_{ls}$ 的单调栈长度。这个可以递归处理。如果右儿子的左儿子的最大值不比 $mx_{ls}$ 大，那么好办，直接递归右儿子的右儿子即可；否则我们可以保证右儿子的单调栈中右儿子的部分肯定能产生贡献，贡献为 $v_{rs} - v_{ls~of~rs}$，我们递归右儿子的左儿子处理左儿子那部分即可。

复杂度：$O(n \log^2 n)$。

Modest Substrings

一个数的权值为 $i,j$ 的数量，使得这个数的第 $i$ 位到第 $j$ 位的数字组成的数的大小在 $L...R$ 内。但是如果第 $i$ 位为 $0$，则无此贡献。

给定上下界 $L,R$，以及数的位数 $n$。需要求出位数为 $n$ 的权值最大的一个数，可以包含前导零。如果有多个解，输出字典序最小的。

$1 \le L,R \le 10^{800},n \le 2000$

AC自动机上DP的神仙题。

如果 $L,R,n$ 很小，可以将 $L...R$ 依次插入AC自动机中，在上面跑DP即可。

首先假设 $L=1$，即不考虑 $L$ 的限制。

我们对 $R$ 建AC自动机。

考虑产生贡献的 $i,j$ 所组成的数长什么样子。大概有三种：

长度小于 $|R|$。
和 $R$ 完全一样。
长度等于 $|R|$，与 $R$ 在一个 lcp 之后的那一位比 $R$ 的位小。

其中前两种比较好算，DP的时候顺便算一下即可。主要是第三种。发现第三种实际上是在AC自动机上跑着跑着跑失配了向上跳了一步，然后这时如果跳的那个边比 $R$ 的对应位小，那么按理来说再往后随便走走剩下位步都会产生第三种贡献。并且AC自动机跳上去以后就不会再计算这种贡献了（因为上面一定都有这个出边，不会失配）

我们可以设 $sum_{p,c,i}$ 表示匹配到 AC 自动机上的 $p$，现在想走 $c$ 边（这是个小于 $R$ 当前位的失配边)，恰好走 $i$ 步后的贡献。这里的贡献指的是 Fail Tree 链上的贡献，即前缀的一些后缀的贡献。这个可以预处理出来。

然后倒着DP（倒着DP好找字典序最小的方案）

设 $f_{p,i}$ 表示跑到 $p$，已经跑了 $i$ 步，接下来跑的最大价值。那么有:

\[f_{p,i} = \max_{c}\{ f_{q,c} + \sum_{i=1}^n sum_{p,c,i} \} \]

（前两种随便做就好）

最终答案为 $f_{0,0}$。

如果考虑 $L$ 的限制的话，可以用 $L-1$ 来容斥，在 $sum$ 上改变即可。建 $R$ 和 $L-1$ 的AC自动机，$R$ 的 $+1$，$L-1$ 的 $-1$。这样的话贡献就是对的了。

复杂度：$O(8000n)$

配对树

整体DP好题。dsu on tree也能做。不过前缀和是真的没想到。

On the Bench

给定长为 $n$ 的序列 $a_i$，问有多少种 $i \to p_i$ 的映射方法，使得映射后的序列 $a_{p_i}$ 中相邻两项之积都不是完全平方数。

$n \le 300,1 \le a_i \le 10^9$

限制等价于将 $a_i$ 中的最大完全平方因子除去后相邻两项不能相同。

现假设值相同的 $a_i$ 之间无标号。（最后需要乘上 $\prod cnt_i$ 变为有标号方案数）那么题意转化为 $m$ 中颜色的球，每种颜色有 $a_i$ 个，共 $n$ 个，同种颜色的球内部无区别，要求相邻的球颜色不同的方案数。

考虑容斥。设 $f_i$ 表示恰好有 $i$ 对相邻的数的方案数，$g_i$ 表示钦定 $i$ 对相邻的数的方案数。钦定的话一种恰好有 $j$ 对相邻数的情况会被统计 ${j \choose i}$ 遍。于是有：

\[g_i = \sum_{j \ge i} {j \choose i} f_j\\ f_i = \sum_{j \ge i} {j \choose i} (-1)^{j-i} g_j \]

最终答案为 $f_0$

现在问题转化为求 $g_j$，即钦定 $j$ 对相邻的方案数。

钦定 $j$ 对相邻可以理解为我们把 $j$ 对球黏一块，剩下 $n-j$ 个球。我们可以枚举每种颜色的球的黏的数量 $b_i$，将 $a_i$ 个球黏 $b_i$ 的方案数等价于将 $a_i$ 个无标号球划分为 $b_i$ 个有标号集合（集合有标号实际上是为了钦定相对位置）的方案数，可以用插板法解决。方案数为 ${a_i - 1 \choose a_i - b_i - 1}$。

最后把每种颜色合并一下，还需要乘多重集排列（其实是一堆组合数乘一块）的系数：

\[g_j = \sum_{\sum_{b_i} = j}\prod_i {a_i-1 \choose a_i - b_i - 1} \times \frac{(\sum_{i}a_i-b_i)!}{\prod_i(a_i - b_i)!} \]

看起来 $a_i-b_i$ 多次出现，那么把 $b_i$ 转化为 $a_i - b_i$：

\[g_j = \sum_{\sum_{a_i-b_i} = j}\prod_i {a_i-1 \choose b_i - 1} \times \frac{(\sum_{i}b_i)!}{\prod_ib_i} \]

然后看到多重集排列想到上EGF：

\[g_i = \prod_i G_i(x)[\frac{x^{n-i}}{(n-i)!}] \]

其中

\[G_i(x) = \sum_k {a_i - 1 \choose k-1} \frac{x^k}{k!} \]

因为 $n$ 非常小，可以暴力卷积。复杂度：$O(n^3)$

Partitions

有 $n$ 个物品，每个物品有一个权值 $w_i$。

定义一个集合的权值 $W(S) = |S|\sum_{x \in S}w_x$。

现需要将这 $n$ 个物品划分为 $k$ 个集合，一个划分方案的价值为 $W'(R) = \sum_{S \in R}W(S)$。

求所有将 $n$ 个物品划分为 $k$ 个集合的的权值和。

$1 \le n,k \le 2 \cdot 10^5,1 \le w_i \le 10^9$

感觉好像省选D1T2？

注意有标号球划分为无标号集合，计数的话需要用第二类斯特林数。

考虑计算第 $i$ 个物品的贡献。可以枚举这个物品所在集合的大小:

\[cost(i) = \sum_{s=1}^n s \times w_i \times {n -1 \choose s-1} \times \begin{Bmatrix} n-s \\ k-1 \end{Bmatrix} \]

然后就可以计算答案了：

\[Ans = \sum cost(i) \]

开始推式子:

\[\begin{aligned} Ans &= \sum_{i=1}^n\sum_{s=1}^n s \times w_i \times {n-1 \choose s-1} \times \begin{Bmatrix}n-s\\k-1\end{Bmatrix}\\ &= (\sum w) \sum_{s=1}^n s {n-1 \choose s-1} \times \begin{Bmatrix}n-s\\k-1\end{Bmatrix}\\ &= W \sum_{s=1}^n s {n-1 \choose s-1} \times \sum_{i=0}^{k-1} \frac{(-1)^{k-1-i}i^{n-s}}{(k-1-i)!i!}\\ &= W\sum_{s=1}^n \sum_{i=0}^{k-1}(s {n-1 \choose s-1}) \times (\frac{(-1)^{k-1-i}}{(k-1-i)!i!}) \times i^{n-s} \end{aligned} \]

那个 $i^{n-s}$ 十分令人讨厌，如果没有它，我们就可以对两个 $\sum$ 分别计算然后乘一起了。

根据省选D1T2的经验，我们看到了组合数和幂和求和，可以尝试去想二项式定理

\[\begin{aligned} Ans = W \sum_{i=0}^{k-1} \frac{(-1)^{k-1-i}}{(k-1-i)!i!} \sum_{s=1}^{n} s {n-1 \choose s-1}i^{n-s} \end{aligned} \]

组合数前面那个 $s$ 也十分令人讨厌，不过我们发现吸收恒等式可以把 $s$ 吸进去，把 $n-1$ 提出来：

\[\begin{aligned} Ans &= W\sum_{i=0}^{k-1}\frac{(-1)^{k-1-i}}{(k-1-i)!i!}\sum_{s=1}^{n} (s-1+1){n-1 \choose s-1}i^{n-s} \\\\ &= W\sum_{i=0}^{k-1}\frac{(-1)^{k-1-i}}{(k-1-i)!i!}(\sum_{s=1}^{n} (s-1){n-1 \choose s-1}i^{n-s} + \sum_{s=1}^{n} {n-1 \choose s-1}i^{n-s})\\ &= W\sum_{i=0}^{k-1}\frac{(-1)^{k-1-i}}{(k-1-i)!i!}((n-1)\sum_{s=1}^{n} {n-2 \choose s-2}i^{n-s} + \sum_{s=1}^{n} {n-1 \choose s-1}i^{n-s})\\ &= W\sum_{i=0}^{k-1}\frac{(-1)^{k-1-i}}{(k-1-i)!i!}((n-1)\sum_{s=1}^{n} {n-2 \choose n-s}i^{n-s} + \sum_{s=1}^{n} {n-1 \choose n-s}i^{n-s})\\ &= W\sum_{i=0}^{k-1}\frac{(-1)^{k-1-i}}{(k-1-i)!i!}((n-1)\sum_{s=2}^{n-2} {n-2 \choose s}i^{s} + \sum_{s=1}^{n-1} {n-1 \choose s}i^{s})\\ &= W\sum_{i=0}^{k-1}\frac{(-1)^{k-1-i}}{(k-1-i)!i!}((n-1)(i+1)^{n-2} + (i+1)^{n-1}) \end{aligned} \]

至此，我们能够在 $O(k \log n)$ 的时间内做完这题了。

杜老师

给定 $L,R$，问从 $L$ 到 $R$ 的数中选择一些数，使得这些数的乘积是完全平方数，共有多少种选法？空集的乘积视为 $1$。多组数据。

$1 \le L \le R \le 10^7,T \le 100,TL:5s$

从质因数分解的角度看，数的乘积是完全平方数，当且仅当这些数的质因数分解种每个质因数的指数的和都为偶数。我们把每个质因数的指数模 $2$，并且把质因数状压一下，就变成了这些数的异或和为 $0$。

看到异或和为 $0$，应该能想到线性基。我们先搞出这些数的线性基，那么任意一种方案就相当于线性基外的数随便选，选好之后就能用线性基的唯一的方式来调整使答案为 $0$。这时一种计数的常见套路（任意选+调整）。因此，答案为 $O(2^{cnt})$。其中 $cnt$ 表示线性基外的数的个数。

然而线性基实在太大，大概是 $O(n^2 / w)$ 的，总复杂度大概是 $O(R-L+1) \times \frac{R^2}{w} $ 。因此我们需要压缩一下线性基。

这时候，大于 $\sqrt R$ 的质数就不幸又被单拎出来了，就像寿司晚宴一样，毕竟它们在一个数中最多只会出现一次。

接下来是个难点：将区间内每个大质数的倍数拎出来，我们现在要求这些数只能出现偶数个。这时我们又可以用开头的那个“调整”的方法了。我们把第一个数打个标记，不将其插入线性基；其余数全部异或上第一个数。这样的话，如果我们选奇数个其余数，那就相当于用一个第一个数来调整一下，使其变为偶数；否则就不用第一个数。

对于小于 $\sqrt R$ 的数就直接暴力线性基就好了。这时线性基的复杂度为 $O((R-L+1) \times \frac{R} w)$。看起来要优秀很多，但是那个 $R-L+1$ 实在太烦人了。

感性理解一下，当 $R-L+1$ 非常大的时候，线性基很有可能是插满的，于是这时我们可以答案是区间长度减去区间内的质因子个数。这个可以 $O(\frac{R}{ \ln R})$ 地对每个质数进行判断。经过打表发现，当 $R-L+1 \ge 6600$ 的时候线性基一定是插满的。

总复杂度:$O(T \min (R-L+1,6600) \times \frac{R}w + T \times \frac{R}{\ln R})$

Binary Cards

给出 $n$ 个需要表示的数 $a_i$，你需要用最少的 $2^k$ 或 $-2^k,k \le 20$，使得能拼出所有需要表示的数并输出方案。

$1 \le n \le 10^5, -10^5 \le a_i \le 10^5$

CF2700的绿题...不过确实是考察分治递归思想的好题！

首先感性理解觉得一个数 $2^k$ 不会被选两次，也不会同时选正和负。（如 $2,-2$ 可以被 $2,-4$ 完全代替；$2,2$ 可以被 $2,4$ 完全代替）

然后比较显然的是，当 $a_i$ 中不存在奇数的时候，就不用选 $1$ 或 $-1$，可以直接将每个数减一递归；否则直接枚举选 $1$ 还是 $-1$，对每种情况都递归一遍。因为递归时每次值域都除 $2$（在去重的前提下），所以有 $T(n)=2T(\frac{n}2)+n$，和归并排序一样，复杂度是 $O(n\log n)$。

posted @ 2020-10-04 14:41 JiaZP 阅读(1048) 评论(0) 编辑收藏举报

刷新页面返回顶部

公告