2-SAT
如果限制条件只是“两者相同”或“两者不同”,问是否有合法方案,那么我们直接用扩展域并查集即可 \(O(nlogn)\) 维护(常数极小,配上按秩合并复杂度还会降低)。甚至我们还可以查询从第几个限制条件开始就没有合法方案了。但是如果限制条件为单向的:若 1 选,则 2 必不选;若 2 不选,则 1 不一定要选。那么我们就只能用2-SAT了。
前置技能:tarjan
图的建立
首先定义:\(X\) 表示选择 \(X\),\(X'\) 表示不选 \(X\); \(X_1 -> X_2\) 表示选择 \(X_1\) 就必须选 \(X_2\)。
我们发现,每一个限制都存在一个逆限制,我们称之为逆否命题,如:\(A->B\) 的逆否命题为 \(B'->A'\),\(A->B'\) 的逆否命题为 \(B->A'\)。这是符合逻辑的。并且我们发现,这是对称的(类似中心对称?反正不像轴对称)。命题与逆否命题的对称性在解决2-SAT问题方面有着重要作用。特别地,\(A -> A'\) 的逆否命题是 \(A -> A'\)(就是它本身)。
我们将所有限制及其逆否命题用有向边来表示出来。
判定是否有解
我们可以认为,对于任意的 \(x\) 和 \(x'\),如果都不在同一个 \(SCC\) 中,那么就一定存在一种解。
由于命题与逆否命题的对称性,如果 \(x\) 能到 \(x'\),那么 \(x'\) 就一定能到 \(x\),使得他们在同一 SCC 里面。
找到解的一种方案
一种简单粗暴容易理解的方法是:先 tarjan 缩点,判断是否有解。如果有解,那么我们在缩点后的 DAG 上跑拓扑序(当然是反图的拓扑)。由于对称性,如果一个点 \(x\) 所在的 SCC 为 1,那么其对称点的 SCC 为 0。可以发现,SCC 实际上也是对称的。因此如果一个点未标记,则将其标记成 \(0\),将其对称点标记成 \(1\)。 否则不管。最后 标记为 0 的点为 “真”,标记为 1 的点为“假”。
另一种改进方法是:因为 tarjan 本质是 dfs,其搞出的 SCC 的编号实际上正是拓扑序。因此我们可以根据 SCC 的编号来决定点为 真 还是 假。
好吧,我已经看不懂上面的东西了,再搞另一种思路吧。
就是tarjan缩点后,对于 \(blong[i][0],blong[i][1]\) ,我们显然要选取拓扑序较大的那一个,因为如果拓扑序较大,那么它就比较靠后,影响的范围更小,更容易构造出方案。
然后tarjan出来的编号其实是拓扑序的逆序,因此我们应该选择编号较小的那一个。
我们规定:\(istrue[cur] = col[cur] > col[opp[cur]]\),其中 \(opp[cur] = cur + n\)。
即:如果“选点”的 SCC 编号较小,就遵从“选”,选择它;否则“不选点”的 SCC 编号较小,遵从“不选”,不去选择它。
证明还是根据对称性。
另一种实现方法
如果不小心在考场上忘记了 tarjan 算法怎么写,或者忘记了方案到底怎么找,还有一种比较暴力的 DFS 做法。不过容易证明这个做法的复杂度也是 \(O(n)\) 的。
随便找一个 \(x\) 和 \(x'\) 都没有遍历过的点 \(x\),沿着它遍历一遍,将遍历过的点都打上 vis 标记,并加入栈中。如果某个时候不合法了,那就退出,把栈中的点的标记都清空,再沿着 \(x'\) 遍历一遍。如果还是冲突,就无解。否则,\(x\) 有 vis 标记就说明选 \(x\),\(x'\) 有 vis 标记就说明选 \(x'\)。
代码:
bool vis[N];
int stk[N], stop;
bool dfs(int cur) {
if (vis[oth[cur]]) return false;
if (vis[cur]) return true;
vis[cur] = true; stk[++stop] = cur;
for (int i = head[cur]; i; i = e[i].nxt) {
int to = e[i].to;
if (!dfs(to)) return false;
}
return true;
}
inline bool work() {
memset(vis, 0, sizeof(vis));
for (int i = 1; i <= n + n; ++i) if (!vis[i] && !vis[oth[i]]) {
stop = 0;
if (!dfs(i)) {
while (stop) vis[i] = false, --stop;
if (!dfs(oth[i])) return false;
}
}
return true;
}
例题
P4782 【模板】2-SAT 问题
\(a || b == true\) 转化为 \(a' -> b\) 和 \(b' -> a\)
吐槽:强制转化是真的慢,去掉(int)istrue[i]后效率高了一倍
当作模板题,贴个板子吧:
for (register int i = 1; i <= n; ++i)
bl[i][0] = i, opp[i] = i + n, bl[i][1] = i + n, opp[i + n] = i;
register int aa, bb, cc, dd;
for (register int i = 1; i <= m; ++i) {
read(aa); read(bb); read(cc); read(dd);
addedge(opp[bl[aa][bb]], bl[cc][dd]);
addedge(opp[bl[cc][dd]], bl[aa][bb]);
}
for (register int i = 1; i <= (n << 1); ++i)
if (!dfn[i]) tarjan(i);
for (register int i = 1; i <= n; ++i) {
if (col[bl[i][0]] == col[bl[i][1]]) {
puts("IMPOSSIBLE");
return 0;
}
istrue[i] = col[bl[i][0]] > col[bl[i][1]];
}
puts("POSSIBLE");
for (register int i = 1; i <= n; ++i) {
printf("%d ", istrue[i]);
}
puts("");
P3209 [HNOI2010]平面图判定
给一个环和一堆边,问是否可能是平面图。
n <= 200, m <= 10000
平面图的边数最多是 \(3 * n - 6\)!
因此 \(n\) 与 \(m\) 规模相同,支持 \(n^2\) 做法。
当然,除去连边操作,剩下的可以 \(O(m)\) 完成。即将边在环外记作 \(1\),在环内记作 \(0\)。然后跑 2-SAT 即可。
P3825 [NOI2017]游戏
题意:
n个地图,有三种赛车 A, B, C,地图分 x, a, b, c 四种场地,其中 a, b, c 分别 不适合 A, B, C 车。每种场地只能使用 A, B, C其中的一种赛车。
现有 m 个限制,为:如果 p 场地使用 P 车,那么 q 场地必须使用 Q 车。
询问是否有解。如果有,输出任意一种方案。
\(n <= 5e4, m <= 1e5, d = \sum[x] <= 8\)
题解:
建立 4n 个点,即将每个场地拆成两个点,然后再给每个点设置个“对称点”。对于 a, b, c 场地以及 m 个限制,使用 2-SAT 模型很容易搞定。但是不好搞的是 x 场地。
发现 x 的数量及其小。那么我们可以枚举 x 场地到底用什么车。但是这样做是 \(O((n + m) * 3^d))\) 的,会超时,并且由于其它场地是“不符合”,而这些场地偏偏是“必须”,实现起来不是很容易。因此我们直接枚举 x 不适合 哪种车,就是说适合其它两种车。这样只用枚举 a, b 场地即可满足所有情况。复杂度: \(O((n + m) * 2^d)\)。
然后就是代码能力+代码能力了。
Ants
这个是线段树优化建图跑 2-SAT,需要用到前缀优化建2-SAT的思想。
前缀优化建图通常解决的问题是,一个集合中如果选了其中一个点,那么其余点都不能选。它大概长这个样子:
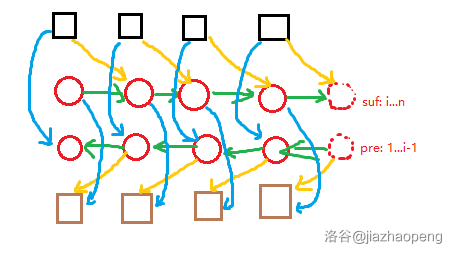
其中两排红点为辅助点,分别表示后缀点和前缀点。黑、棕色方点为原始节点。
线段树优化建图的问题则是,一个线段树节点内存着若干个点,如果选了其中一个点,那么其余点都不能选,且线段树的祖先节点内的点和子树内的点也不能被选。它大概长这个样子:
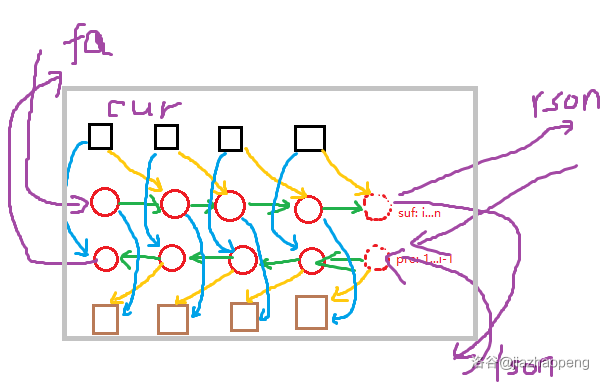
大概就是把父子的串给连起来。
需要注意的是,这种方法的节点数特别多,点数和边数都是 \(O(n \log n)\) 级别的。这道题是树剖套线段树,所以是 \(O(n \log^2 n)\) 的。
此外,在这道题中我尝试 p << 1 和 p << 1 | 1 来表示一个点的两种决策,看起来是非常方便的,连边可以写一个 Addedge,里面套两个 addedge,就不怕少连边使得不对称了。
习题
注意:
开大数组!!!!
附:
tarjan求强连通分量
void tarjan(int cur) {
dfn[cur] = low[cur] = ++dcnt;
stk[++stop] = cur; vis[cur] = true;
for (register int i = head[cur]; i; i = e[i].nxt) {
int to = e[i].to;
if (!dfn[to]) {
tarjan(to);
low[cur] = min(low[cur], low[to]);
} else if (vis[to]) {
low[cur] = min(low[cur], low[to]);
}
}
if (low[cur] == dfn[cur]) {
int tmp; ctot++;
do {
tmp = stk[stop--];
col[tmp] = ctot;
vis[tmp] = false;
} while (tmp != cur);
}
}
2-SAT 基本操作
for (register int i = 1; i <= n; ++i)
bl[i][0] = i, bl[i][1] = i + n;
//...(addedge)
for (register int i = 1; i <= (n << 1); ++i)
if (!dfn[i]) tarjan(i);
for (register int i = 1; i <= n; ++i) {
if (col[bl[i][0]] == col[bl[i][1]]) {
puts("IMPOSSIBLE");
return 0;
}
istrue[i] = col[bl[i][0]] > col[bl[i][1]];
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号