容斥(含min-max容斥)
资料与前置知识
组合数学
博客:初探容斥原理 容斥的原理及广义应用
二项式定理
二项式反演:
若
则
具体见组合数学
容斥入门(小学奥数版)
容斥的基本思想:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复
简单容斥:
这样,我们如果能够轻易知道A“并且”B的答案,就可以龟速地算出A“或者”B的答案;如果能够轻易知道A“或者”B的答案,就可以龟速地算出A“并且”B的答案
例题:
Jordan 筛法(几乎不用)
在 \(n\) 个集合中,选出恰好属于 \(m\) 个集合的元素个数:
这涉及到了容斥的本质,见下图:(来源:qy学长的课件)
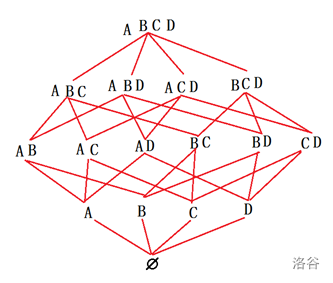
其中字母表示元素/集合,\(AB\) 表示 \(A ∩ B\) 中不属于 \(C,D\) 的部分,即仅属于 \(A ∩ B\) 的部分。
这样, \(A ∩ B = AB + ABC + ABD + ABCD\)(类似一个DAG上的可达点)
由于是个DAG,可以根据 \(A ∩ B,A ∩ C,...\) 的值来反推 \(AB,AC,...\) 的值。由此,可以确定容斥系数。
递推方程:“恰好”(目标) = val[cur](递推系数) + 所有“前驱”的 val
(hard)容斥系数的确定
#2839. 集合计数
先放式子:
首先我们将交集至少为 \(k\) 的方案数算出来,为:\(C_n^k * (2^{2^{n-k}}-1)\)(先确定 \(k\) 个数,再其它数随意)
针对我们钦定的 \(k\) 个数,发现多加了交集为大于等于 \(k + 1\) 的情况,先考虑 \(k + 1\):先选出多算的那 \(k + 1\) 个的情况是什么情况,即选出多算了哪一个数。然后其它数任选即可。这里看似一切正常。对应的式子为 \(- C_{n-k}^1* (2^{2^{n-k-1}}-1)\)
然后考虑交集大小为 \(k + 2\) 的情况:先选出多算的那两个数是哪两个数,然后考虑它已经被算了几次。\(k\) 的时候算了一次,两个多出来的数中每一个数都会被 \(k + 1\) 的时候减掉一次,这样它被算了 \(1 - C_2^1\) 次。看似毫无规律的样子...不过,经过化简,我们发现它被算了-1次,而它的目标系数为0,那么我们把它加一下就好了。这里已可以窥探出一些规律。对应的式子为 \(+C_{n-k}{2}* (2^{2^{n-k-2}}-1)\)
然后考虑交集大小为 \(k + 3\) 的情况:照常套路,但是我们要知道它已经被算了多少次。k的时候被加了一次,然后三个多出来的数中 每一个数 都会被 \(k + 1\) 减掉一次,然后 每两个数 都会被 \(k + 2\) 加上一次。注意到“每x个数”,我们想到了基础容斥的那种情况。换言之,它被算了 \(C_3^0 - C_3^1 + C_3^2\) 次。看它不爽,加上个 \(-C_3^3\),为 \(C_3^0 - C_3^1 + C_3^2 - C_3^3\),这玩意恰恰等于0(组合恒等式),并且0恰好为目标系数。那么只需加上个 \(-C_3^3\) 的容斥系数就好了。规律可见,是加是减取决于当前 \(k + x\) 中x的奇偶。因此得出上面的式子。
容斥基础 (雾)
(小热身)
有一个集合S,如果枚举它的每个子集,即:(其中 $sum[T] $ 表示集合T内元素值的和)
那么每个元素的贡献为:(枚举含x的集合大小)
考虑每个元素的贡献时 min-max 容斥证明的常用思想。
min-max容斥:
t为s的非空子集, \(min(s)\) 表示集合中元素最小值, \(max(s)\) 表示集合中元素最大值:
当 \(|s|=1\) 时很好理解;
当 \(|s|=2\) 时也很好理解:比如s={1, 5},那么 \(max(1, 5)=1+5-min(1,5)\), \(min(1, 5)=1+5-max(1, 5)\)
当 \(|s|=3\) 时或许也还行:比如s={2, 3, 5},那么
当 \(|s|>3\) 时就要背结论了。
以 \(max(S)=\sum{min(T)* (-1)^{|T|+1}}\) 为例:
我们要求一个函数 \(f(x)\),使得:
考虑每个数 (第 x + 1 大) 的贡献次数:
二项式反演:
由于 \(ismx(i)=[i==0]\),因此:
即
所以
对于期望min-max也同样适用,即:
其中
\(E(max(s))\) 表示 s 集合内随机变量(期望几次能出现某元素) 的最大值,即期望几次能取完 s 集合;
\(E(min(s))\) 表示 s 集合内随机变量(期望几次能出现某元素) 的最小值,即期望取几次能包含 s 的一部分,即第一次取到s集合中元素的期望次数。
它的应用见下一道例题:
例题:P3175 [HAOI2015]按位或
大概需要知道:
-
min-max定理
-
若对于随机变量x:(k>0,k为整数)
则有:
最后一步等比数列乘等差数列 可以用错位相减法推出。
好像称之为:离散随机变量的几何分布(见题解)
因为 “某集合元素出现的期望最小值” 这个随机变量只能取正整数(尽管它的期望不是),因此是“离散随机变量”,可以套用这个公式。
- FWT_or搞子集问题
Code:
read(n); All = (1 << n) - 1; limi = All + 1;
for (register int i = 0; i <= All; ++i) {
scanf("%lf", &A[i]);
}
FWT_or(A);
init_ct();
double res = 0;
for (register int s = 1; s <= All; ++s) {
if (F(1.0 - A[All ^ s]) <= eps) failed(s);
res += 1.0 / (1.0 - A[All - s]) * (ct[s] & 1 ? 1 : -1);
}
printf("%.12lf\n", res);
例题:喂鸽子
求 \(E(\max_{i \in S}(x_i))\),其中 \(x_i\) 表示到 \(i\) 吃饱所需次数。设随机变量 \(X\) 表示出现饱鸽子的时间。
其中 \(f_t(k) = [\frac{x^k}{k!}](\sum_{i \le K}\frac{x^i}{i!})^t\)
kthmin-max(扩展min-max)
先直接抛出结论:
证明
以 \(kthmax(S)=\sum{min(T)~* ~C(|T|-1,k-1)~* ~(-1)^{|T|-k}}\) 为例:
我们要 求一个函数 \(f(x)\),使得:
考虑每个数 (第 \(x + 1\) 大) 的贡献次数:
二项式反演:
由于 \(iskthmx(i)=[i==k-1]\),因此:
即
所以
记忆:你看T是大写的,那么就把 |T| 当作比 k 大的数,然后C(-1,-1)和 ^(|T|-k) (大雾)
- 扩展min-max也可以用到期望中去,即:
于是就有了下面的例题:
P4707 重返现世
每个单位时间,这片地域就会随机生成一种原料。每种原料被生成的概率是不同的,第 i 种原料被生成的概率是 \(\frac{p_i}{m}\) 如果 Yopilla 没有这种原料,那么就可以进行收集。
Yopilla 急于知道,他收集到任意 k 种原料的期望时间,答案对 998244353 取模。
题目要 求: \((n-k+1)thmax(All)\)
将 \(n-K+1\) 用 \(K\) 来表示,此时 \(K <= 11\),套用期望kthmin-max公式:
其中\(P(min(T))=\frac{\sum p_t}{m}\),每次只选一个,因此\(E(min(T))=\frac{1}{P(min(T))}=\frac{m}{\sum{p_t}}\),(其中 \(p_t\) 为 \(T\) 中元素 \(t\) 的概率)。
发现 \(n,m,K\) 很小,可以考虑以这些为状态做dp。
设 \(f[i][k][j]\) 表示只考虑前 i 个,的 \(E(kthmax(S_i))\) 的式子中的\(E(min(T))=\frac{m}{\sum{p_t}}=\frac{m}{j}\) 时的 \(C(|T|-1,k-1)~* ~(-1)^{|T|-k}\)的值(因为这样同分母,好算好转移)。
这样,最终答案为:\(\sum_{j=1}^{m} ({\frac{m}{j}~* ~f[n][K][j]})\)
考虑转移。
如果第i个元素不加入所谓 \(T\) 集合中,那么继承前 \(i-1\)个:\(f[i][k][j] = f[i - 1][k][j]\);
剩下考虑第 \(i\) 个元素加入所谓 \(T\) 集合中:
发现 \(f[i][k][j]\) 只能从 \(f[i-1][?][j-p_i]\) 中转移而来。我们再看一下式子:
如果加上个 \(i\) ,那么就变成了:
\(-1\) 的指数加1还好,只是正负变一下,但组合数变一下就不大妙了。但我们根据杨辉三角(或许是),即 \(C(n, m) = C(n - 1, m - 1) + C(n - 1, m)\) ,这样就可以拆掉了。
总递推式为:
发现复杂度可行。第一维可以滚动数组优化,也可以用类似背包一样的做法优化。
最后说一下边界:\(f[0][0][0] = 0; for (k:1->m) f[0][k][0]=-1\) 至今未想通。。。
(思维量与代码量不成正比)
\(Code:\)
for (register int i = 1; i <= K; ++i) f[i][0] = -1;
for (register int i = 1; i <= n; ++i) {
for (register int j = m; j >= p[i]; --j) {
for (register int k = K; k; --k) {
f[k][j] = (f[k][j] + f[k - 1][j - p[i]] - f[k][j - p[i]]) % P;
if (f[k][j] < 0) f[k][j] += P;
}
}
}
ll ans = 0;
for (register int j = 1; j <= m; ++j) {
ans = (ans + f[K][j] * quickpow(j, P - 2)) % P;
}
printf("%lld\n", ans * m % P);
Continued...


 浙公网安备 33010602011771号
浙公网安备 33010602011771号