后缀自动机(SAM)
重要资料
OI-wiki:后缀自动机 (SAM)
基础、概念部分
Right集合(endpos集合):
Right = 能到达该节点的子串出现的右端点集合 = 想匹配的话,当前可能在的位置集合
-
两子串的Right集合,要么包含,要么不交(树形),suffix link 指向的是树中的父亲。
-
Right集合相同,则后续转移相同,因此在SAM中压成一个点(完全不懂)
-
len:同一Right集合中最长子串
简单的说, \(Right\) 集合可以看作从根节点走到该节点的所有路径的子串集合在原串中的结尾位置集合。
len:节点所代表的最长子串
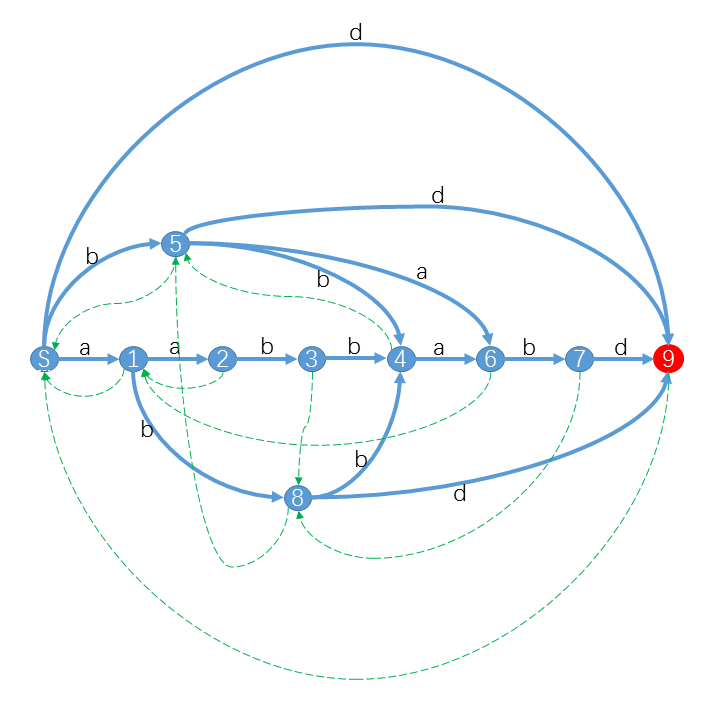
每个节点能表示的子串长度为 \([~len[fa[cur]] + 1 , len[cur]~]\)。结合下图理解:

其中 1 是 6 的 \(fa\)。由于 6 往后的 DFA 再也无法回到 6 以及 6 以前,因此上一个点(5)的 \(len\) 加 1 就是 6 的 \(len\),即 \(maxlen\)。由于想要到达 6 的最小路径是从 \(fa\)(2) 直接沿着 \(a\) 边走下来,字符串长就是 \(fa\) 再加上 1.
值得注意的是, \(ins\) 时一旦建立了一个节点,它的 \(len\) 就基本不会再变了,但是 \(endpos\) 集合会经常变动。因为以后再加字符时,还可能会出现当前节点所代表的字符串,还会将 \(suffix ~ ~ link\) 指向该节点。
注意:确切地说,每个节点的 \(endpos\) 集合,实际上时该节点所代表的子串的 \(endpos\) 集合。 由于某种原因,这些子串的 \(endpos\) 集合相同。
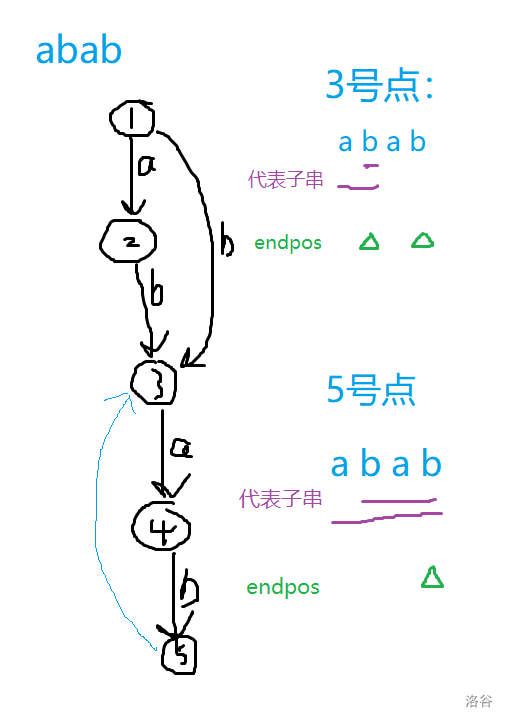
用一张图来说就是:
一些常识
-
相邻节点,len长的,endpos短。因此拓扑排序通常以len排序
-
\(minlen(cur) = len(fa[cur]) + 1\)
-
一个点在Parent Tree到根节点的路径所经过的点的代表子串(指能到达那些点的串)所组成的集合为一个后缀。
-
如果想要多次查询一个串的子串\([L, R]\)的接受点,可以首先找到[1,R]的接受点,然后往上倍增找到最靠上的 \(len <= R - L + 1\) 的点,那个点即为\([L,R]\)的接受点。
主要还是背板子,结合O(n^2)的后缀树理解。
两种操作:加一个叶子节点,在边上加一个点。
重点记忆:
fa[nq] = fa[q]; fa[np] = fa[q] = nq;
while (son[p][c] == q) son[p][c] = nq, p = fa[p];
辅助记忆拆点部分代码:
//拆点:为了防止一些串搞怪,
//把代表子串长度为len[p]+1 -- len[q] 的q点拆成
//len[p] + 1 和 len[p]+2 -- len[q]的点
1. 新建节点
2. len[nq] = len[p] + 1 不难理解
3. 因为nq和q都是由一个点拆出,所以nq的son,fa与q相同
4. 由于nq的len较小,所以endpos集合位置较多。
实际上,nq的endpos包含q的endpos。
根据SAM的fa边都是由endpos少的点指向endpos多的点
(len长的点指向len短的点)
所以需要fa[q] = nq;
又因为nq的endpos包含q的endpos,也包含np的endpos,
所以根据树形,fa[np] = nq。
5. 沿着p的fa,将(son)指向q的点都指向nq。
其余基本可以理解记忆。
模板题:P2408 不同子串个数(感觉这道题要比洛谷模板题更板一些)
Code:
inline void ins(int c) {
int p = lst, np = ++tot;
lst = np; len[np] = len[p] + 1;
while (p && !son[p][c]) son[p][c] = np, p = fa[p];
if (!p) return fa[np] = 1, void();
int q = son[p][c];
if (len[p] + 1 == len[q]) return fa[np] = q, void();
int nq = ++tot;
len[nq] = len[p] + 1;
memcpy(son[nq], son[q], sizeof(son[q]));
fa[nq] = fa[q]; fa[np] = fa[q] = nq;
while (son[p][c] == q) son[p][c] = nq, p = fa[p];
}
注意!!!
-
一定要加lst = np。注意,是np,不是p!!!
-
数组要开二倍!!
-
while(p && !son[p][c])不要和while(son[p][c] == q)弄混了,可不是while(p && son[p][c] != np)!! -
一定要
p = fa[p]!!!
SAM的应用
识别长串的子串
直接在 DFA 上跑。每个节点都是接收节点。如果跑着跑着突然没有 \(c\) 出边了,那就说明识别失败了;否则顺利跑完小串,就说明是长串子串。
最小循环移位
暴力方法:倍长字符串,在字符串的前n个位置开始往后跑 \(n\) 个字符,取字典序最小。
优化方法:每次跑的 \(n\) 个字符都是倍长后字符串的子串,因此可以直接建一个倍长后字符串的后缀自动机,在 DFA 上挑字典序最小的路径跑 \(n\) 步。
某节点所代表(本质不同)子串的个数 / 本质不同子串总数
例题:
P2408 不同子串个数(即上面提到的模板题)
由于“代表”这个词的意思不清,dp 方法中“代表”指的是能从该节点向下转移的总方案数(通常包含不动的情况),而SAM 的方法中“代表”则指的是有多少个串能够到达该节点,和 \(Right\)集合(\(endpos\) 集合)有关。因此这里主要讲如何求本质不同的子串总数。
方法一:DP
某节点的后续转移数 \(=\) 在 DFA 上从该节点往下走的路径总数 \(+\) 1(不动也算一种路径,就相当于直接被识别了)
由于 DFA 为有向无环图,因此可以dp搞:
可以按 \(len\) 拓扑排序,也可以直接记忆化搜索。拓扑排序或许更快。
最终答案为根节点的 \(f\) 再减一(除去空串)
方法二:利用SAM的性质
某节点所代表子串的个数 \(=\) 其所代表子串长度范围 \(= len[x] - (len[fa[x]] + 1) + 1~ ~ ~ ~ = ~ ~ ~ ~len[x] - len[fa[x]]\)
依据:\(minlen[cur] = len[fa[cur]]~ + ~1\)
由于 SAM 的优秀性质:不同节点所代表的子串一定本质不同,因此 本质不同子串总数 \(=~ \sum\) 某节点所代表(本质不同)子串的个数
对于动态求子串总数,要是硬维护 \(\sum len[cur] - len[fa[cur]]\),也不是不可做。但有更简便的方法:每加一个字符,新增的子串肯定是该串的一个后缀,并且肯定 \(endpos\) 只有 \(len\)。因为如果 \(endpos\) 还有一个前面的,那说明这个子串已经出现过了。因此直接:\(ans += len[lst] - len[fa[lst]]\) 即可。
\(Code:\)
不同子串个数 :略。
生成魔咒:my record
所有不同子串出现总长度
方法一:DP
某节点所代表子串个数 \(f[cur]\) (从 \(cur\) 往后走(含呆在 \(cur\) 不动),能得到的子串数)可以通过上面的方法得出。
设 \(ans[cur]\) 为 在 DFA 上,从 \(cur\) 往后走,能走到的所有子串的长度之和。那么有:
依据:每条路径子串的长度都 \(+1\)(含静止不动)
方法二:利用 SAM 的性质
容斥:用 \(cur\) 代表的子串总长度 \(- fa[cur]\)所代表的子串长度 即可。
注:这里的 “\(cur\) 代表的子串总长度” 实际上并不是真正\(cur\) 代表的子串总长度,而是从空串到它代表的最长子串。事实上应该是\(minlen[cur] -> len[cur]\)。反正是等差数列,随便算算即可。
注意:
以上两种方法,第一种是根据以后的路径来考虑的,第二种是根据之前怎么来的来考虑的,实际上并不太一样。
第k小子串
或许SA更方便些?
例题:SP7258 SUBLEX - Lexicographical Substring Search
求本质不同的子串中第 \(k\) 小子串。多次询问。
搞出每个点往后有几种转移方式(字符串),然后充分运用贪心思想,学着Splay搞第k小即可。
注意站着不动也算一种转移方式,并且是字典序最小的转移方式。
注意根节点的特判。
\(Code\):my record
查询小串在大串中的第一次出现位置
问题可以转化成 \(endpos\) 集合里的最小值。
当 \(cur\) 为 \(np\) 时,\(firstpos[cur] = len[cur]\);当 \(cur\) 为 \(nq\) 时, \(firstpos[cur] = firstpos[q]\)。
类似证明在“某子串出现次数”中。
注意,这里的 \(firstpos[]\) 为小串的结尾位置;一般要求小串的开头位置,稍作转化即可。
查询小串在大串中的所有出现位置
绝妙的解释:oi-wiki
就是说,每个节点的 \(endpos\) 集合,(假设)一定是由许许多多的子树节点的 \(firstpos\) 组合在一起的,因此最简单的方法就是在 \(parent\) 树上跑子树的 \(firstpos\),然后去重。
但是要去重。因为可能会有两个可能有相同 \(endpos\) 值的不同状态(摘自 oi-wiki,但我觉得这里的 \(endpos\) 应该改为 \(firstpos\))。如果一个状态是由另一个复制而来的,则这种情况会发生。所以我们可以直接忽视掉 \(nq\)。
这可能要我们真的建出 \(parent\) 树,但这并不难。
例题:CF1037H Security
这道题关键在于查询长串的 [l, r] 内是否出现某子串。
直接用权值线段树维护每个节点的 \(endpos\) 集合。如果存在该子串,那么一定有 $pos $ ∈ \([l, r]\),且 \(pos - len + 1\) ∈ \([l, r]\)(\(pos\) 为 某一 \(endpos\))
需要适用线段树合并。这里有一个小技巧,就是我们只需要知道某节点管辖范围内有没有数,因此我们不需要维护\(siz\)之类的东西,直接利用动态开点权值线段树的特点,如果有这个点,那么有它一定是有原因的,一定曾在这个点添加过数,因此直接返回true即可。
int merge(int L, int R, int cur1, int cur2) {
if (!cur1 || !cur2 || L == R) return cur1 | cur2;
int mid = (L + R) >> 1, nwcur = ++ttot;
ls[nwcur] = merge(L, mid, ls[cur1], ls[cur2]);
rs[nwcur] = merge(mid + 1, R, rs[cur1], rs[cur2]);
return nwcur;
}
bool query(int L, int R, int l, int r, int cur) {
if (!cur) return false;
if (l <= L && R <= r) return true;
if (R < l || r < L) return false;
int mid = (L + R) >> 1;
return query(L, mid, l, r, ls[cur]) || query(mid + 1, R, l, r, rs[cur]);
}
inline void Merge() {
for (register int i = tot; i; --i) {
int p = id[i];
if (fa[p]) rt[fa[p]] = merge(1, s_n, rt[fa[p]], rt[p]);
}
}
inline bool che(int p, int ll, int rr, int nwlen) {
if (rr - (ll + nwlen - 1) + 1 <= 0) return false;
return query(1, s_n, ll + nwlen - 1, rr, rt[p]);
}
当然也可以用主席树做,发现每次我们只要知道一个节点的子树(\(Parent\) 树上)的某个区域内有没有 \(endpos\);如果搞到 \(dfn\) 序上,那么我们实际上就是在查询某一区间上的集合中 在某一区域内 有没有 \(endpos\)。然后可以前缀和+差分转化成 权值线段树可做的问题。
这个问题还是很常见的(或许?),NOI也考过:P4770 [NOI2018]你的名字
某子串出现次数
某子串出现次数 = 代表该子串的节点的 \(endpos\) 集合的大小
- 求法:
在 \(ins\) 时,将 \(np\) 的 \(siz\) 标为 \(1\),将 \(nq\) 的 \(siz\) 标为 \(0\).然后按 \(len\) 拓扑排序。在 \(parent\) 树(由 \(fa(suffix links)\) 组成)上跑,\(siz[to] += siz[cur]\);
具体讲解见:史上全网最清晰后缀自动机学习(三)后缀自动机里的树结构
以及:oi-wiki
感觉里面讲得不错。
\(Code:\)my record
简单(假)证明:
(感觉说不清楚的样子)新建节点时,它的 \(endpos\) 集合大小肯定是 \(1\)。但是随着 \(ins\) 函数的进行,它的 \(endpos\) 集合在改变。
比如说有个 \(len = 4\) 的点向它连 \(suffix ~ link\),它的 \(endpos\) 成功变成 {\(2, 4\)}。最后我们处理时会让 \(len = 4\) 的节点给它贡献一个 \(1\),再加上原本的那个 \(1\),就能算出 {\(2,4\)}的 \(endpos\) 集合大小了。
再有一个 \(len = 6\) 的节点指向它也差不多。
为什么不能让 \(siz[nq] = 1\) 呢?因为我们并不能保证 \(nq\) 的最小 \(endpos\) 是自己给自己贡献的,就像上面的 \(2\) 一样,它的每个 \(endpos\) 应该都是 \(parent\) 树上的儿子贡献的。毕竟 \(nq\) 只是硬生生地根据 \(len\) 把一个节点分成了两个,然后让原节点指向它,并且再加一个节点。
实在不行感性理解吧。

第k小子串(加强版)
求所有子串中第 \(k\) 小子串。(本质相同,位置不同的子串算多次)
继续搞出每个点往后有几种转移方式(字符串),只不过本质相同,位置不同的子串算多次。
找第 \(k\) 小子串时也要判断一下:
if (np != 1) k -= siz[np];
(np = 1时,空串不算串,不占用排名的名额)
其余和之前基本相同。
\(Code\):my record
最短的 没有出现的 字符串
把该字符串放到 DFA 上跑,无法被 DFA 接受。
如果在长串中没有出现某一字符,即 DFA 上的初始节点没有 \(c\) 的出边,那么答案肯定就是 \(c\),否则要找初始节点所有出边中最优的出边,即需要向后加最少字符才能使字符串不被 DFA 接受 的出边。
用 DP 来解决。在 DFA 上 dp:
当存在无某一出边时:\(d[u] = 1\)
否则:\(d[u] = 1 + min(v)\) (\(son[u][c]=v\))
依据 \(d\) 数组,我们可以推出字符串到底是什么。
求两串的最长公共子串
例题:SP1811 LCS - Longest Common Substring
给出 \(S\) 和 \(T\),求 \(S\) 和 \(T\) 的最长公共子串。
考虑从 \(T\) 的每个前缀中找出 其各个后缀中属于 \(S\) 的子串的最长后缀,答案就是所有最长后缀中最长的那个。(有点绕口)
怎么找后缀中属于 \(S\) 的子串的最长后缀呢?既然属于 \(S\) 的子串,那么那个后缀一定能被 \(S\) 的 DFA 识别。我们要在此基础上,删去尽可能短的前缀,留下尽可能长的后缀。
充分运用贪心,只要能走 \(c\) 边,就走,并且 \(mxlen++\),否则:
先要保证能被识别,于是不断跳 \(fa\),直到可以走为止;
再要保证尽可能长,因此修改 \(len\) : \(mxlen = len[cur]\)
(因为如果我们不幸跳了 \(fa\),我们将有多个子串可以选择。这些子串在原 \(S\) 串上是连续的(“连续”啥意思见开头图,即末尾相同),并且长度是一段连续的区间。出于贪心的想法,我们自然要选择最长的那个子串)
记得要往下走!因此实际上是 \(mxlen = len[cur] + 1\),但在代码中可以合并,一会儿看代码就知道了。
答案为所有 mxlen 中的最大的那个。
关键代码:
int ans;
inline void sol() {
int p = 1, mxlen = 0;
for (register int i = 1; i <= n; ++i) {
int c = s[i] - 'a';
while (p && !son[p][c]) p = fa[p], mxlen = len[p];
if (!p) {
mxlen = 0, p = 1;
continue;
}
p = son[p][c]; mxlen++;
ans = max(ans, mxlen);
}
}
两串的公共子串个数
例题 : P4770 [NOI2018]你的名字
题意:给出一个长串 \(S\) ,然后给出一堆短串 \(T\),给 \(T\) 同时给出 \(L, R\),询问有多少串 不属于\(S\) 的子串,但属于 \(T\)的子串。
可以转化成求两串的公共子串个数。
转化成对于 \(T\) 的每个前缀,求有多少串是 \(S\) 的子串。然而还不对,最后还要去重。
去重可以在 \(T\) 的后缀自动机上进行。
具体来说,对于 \(T\) 的 \(SAM\) 上的每一个节点,记录一下其管辖的子串(指的是从根能到达的子串)中有多少子串属于 \(S\) 的子串。
发现对于每个节点 \(cur\),其管辖范围的子串是连续的(前面已经提到过);如果其中某个长串属于 \(S\),那么其子串一定是 \(S\) 的子串。因此我们转而求 每个节点中最长的 属于 \(S\) 的子串的串长度。 我们记此为 \(mx[]\)。
求每个前缀在 \(S\) 中的最长子串?已经就有点 求最长公共子串 的意思了。
还是那样,每拓展一个字符,\(S\) 的 \(DFA\) 上最多往下跑一个节点;如果一个可以跑的节点都没有,就尝试往 \(fa\) 上跳(类似\(AC\)自动机),再进行尝试。往 \(fa\) 上跳,就说明我们的子串变小了,那么 \(T\) 上自动机的点可能(肯定)就不合法了(比如 \(abbaa\) 变成了 \(baa\))。怎么办呢?
幸运的是,我们发现,因为我们跳 \(fa\) 只会砍掉开头的几个字母,串的 \(endpos\) 还是那几个,可能还会多一些。那么我们就在 \(T\) 的自动机上跳 \(fa\)。最后找到合法的 \(S\) 位置和合法的 \(T\) 位置后,用 \(nwlen\)(当前串长度)来更新 \(mx[]\) 即可。
和下面(求多串的最长公共子串)同理,如果 \(T\) 上某一个节点能匹配 \(nwlen\),其祖先也可以匹配 \(nwlen\),但是不能超过其 \(len\)。
我们离线搞或许也可?题解里面给出了一种在线的做法:就是说更新没多久,某个节点的 \(mx[]\) 变成了 \(len[]\),那么其所有祖先肯定也被更新成了 \(len[]\),所以我们暴力跳链,知道 \(mx[]=len[]\)停止。复杂度正确。
总结一下:
-
建立 \(S\) 和 \(T\) 的 \(SAM\)。
-
在 \(S\) 的自动机上跑 \(T\)(以 \(AC\) 自动机的跑法),找到当前前缀的合法(公共)后缀(实际上是找到了 \(S\) 的合法位置)。
-
同时在 \(T\) 上跑,并且检查 \(T\) 上的位置是否合法,并更新所有合法位置的 \(mx[]\)
-
所有的 \(max(mx[cur] - len[fa[cur]], 0)\) 之和即为答案。
另外说明一下,NOI2018这道题还结合了 查询子串是否在 \([L, R]\) 区间内 的问题,此问题与CF1037H Security 问题类似,故不过多讲解。
但是需要注意的是,在完成这道题的时候,不能像while (np_s && (!S.son[np_s][c] || !che(l, r, np_s, nwlen))) np_s = S.fa[np_s]一样跳,因为有了 \([L, R]\) 的限制,我们无法匹配可能是由于 \(nwlen\) 太长造成的,但直接跳 \(fa\) 是不合适的。比如 \(aabaa, abaa, baa\) 的节点,如果 \(aabaa\) 不合法,\(abaa\) 和 \(baa\) 是有可能合法的(可能正好卡在 \([L, R]\) 的边缘),因此我们应该不断尝试缩小 \(nwlen\),小到小于该节点的最小串后再跳 \(fa\)。
普通的求 两串公共子串个数 应该不用这样做。
\(Code:\)my record
int np_s = 1, np_t = 1, nwlen = 0;
int ct = 0;
for (register int i = 1; i <= t_n; ++i) {
int c = s[i] - 'a';
while (np_s && !S.son[np_s][c]) np_s = S.fa[np_s]
nwlen++;
np_s = S.son[np_s][c]; np_t = T.son[np_t][c];
while (T.len[T.fa[np_t]] + 1 > nwlen) np_t = T.fa[np_t];
int p = np_t;
while (T.mx[p] != T.len[p] && p)
T.mx[p] = max(T.mx[p], min(nwlen, T.len[p])), p = T.fa[p];
}
for (register int i = 2; i <= T.tot; ++i) {
res -= max(T.mx[i] - T.len[T.fa[i]], 0ll);
}
求多串的最长公共子串
SP1812 LCS2 - Longest Common Substring II
SP10570 LONGCS - Longest Common Substring
对其中一个串做 SAM,然后还是上回的思路,只不过这我们要记录每个节点的匹配的最大值,然后众串取个最小,最后每个节点取个最大。
众所周知,每个节点代表一些长度连续的区间,我们的任务是找出每个其他串能匹配的最长长度,这样,能匹配长度为 4 的子串就一定能匹配长度为 3 的子串,但能匹配长度为 3 的子串不一定能匹配长度为 4 的子串.因此我们需要各串的答案中取个最小值,这个最小值所代表的串一定在所有串中出现。
最终把所有这样能在所有串中出现的局部最大值(对于每个节点而言)再取个 \(max\) 就是全局最大值(对于所有串而言)。
然而会被 \(hack\) 掉。
abcba
ab
ba
答案显然是1("a"或"b"),但看看我们做的好事:

我们只经过了 \(5,6,2,3\) 节点,并且每个都只经过了一次,答案当然为 0.
哪里有问题?发现 6 节点答案一定可以作为 2 节点答案,因为 2 节点的串全是 6 节点的串的子串,6节点的 \(abba,bba,ba\) 中能搞到长度为 2 的最长公共子串,那么 2 节点的 \(a\) 就也应该能搞到长度为 2 的子串(如果有的话);又因为 2 节点最长才为 1,所以需要和 1 取一个 \(min\)。
是不是有点像 AC 自动机的部分操作?
总结一下:
首先对一个串建立 SAM
然后把其他串拿过来再 SAM 的 DFA 上跑,并记录每个节点能搞到的最长长度。
接着我们把每个节点的最长长度传递给 \(fa\)(当然是按照 \(len\) 递减的顺序),并且更新当前节点的公共长度(取 \(min\))。
最后我们找出所有节点公共长度的最大值,作为答案。
\(Code:\)
//for every other string
int p = 1, res = 0;
for (register int i = 1; i <= n; ++i) {
int c = s[i] - 'a';
while (p && !son[p][c]) p = fa[p], res = len[p];
if (!p) {
res = 0, p = 1;
continue;
}
res++; p = son[p][c];
nwmx[p] = max(nwmx[p], res);
}
for (register int i = tot; i; --i) {
int p = id[i];
nwmx[fa[p]] = max(nwmx[fa[p]], min(len[fa[p]], nwmx[p]));
mn[p] = min(mn[p], nwmx[p]);
nwmx[p] = 0;
}
//at last
for (register int i = 1; i <= tot; ++i) {//only one string
ans = max(ans, mn[i]);
}
求多串的公共子串数量
并没有找到相关题目和题解,只有一个这个
我的大致思路是 结合前三种问题。第二种问题我们拿到 \(T\) 上搞,主要是因为 \(S\) 太长了,一个就 \(5e5\);并且询问太多了,一共有 \(1e5\) 次询问,并且每次询问还有不同的 \(L, R\),不好离线。
如果不含 \([L, R]\) 的限制的话,第二种的本质其实和第一种问题相同,只不过是求每个节点(\(S\)上)的 \(mx[]\)。方法和第三种问题类似。
那么求多穿的公共子串数量是否也可以搞出每个 \(S\) 节点上的 \(mx\),最后一汇总?
我想是这样的(未经检验)
那么代码应该和第三种类似,只不过最后不是取 \(max\),而是加和。
注意要减掉 \(len[fa[cur]]\) 以防计重。
好吧,只是我瞎想的
一些例题
对子序列这样的东西也可以建一个自动机:\(son[np][c]\) 指向下一个 \(c\) 的位置。
二分答案,问题转化为在一个大串里面查询一个小串是否出现。倍增快速查子串接受点+线段树合并查endpos。
错误
1
len[nq] = len[q] + 1;
2
len[np] = len[p] = 1;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号