tarjan 算法与图的连通性

前言与预备知识

发现我根本不会 tarjan，又发现《算法竞赛进阶指南》上正好有相关讲解，于是回来补 tarjan 这个 NOIP 算法。 ~~（顺便颓一会儿水题）~~

首先我们要知道 搜索树 的相关内容（注意区分搜索树和原图）：

定义 \(dfn[cur]\) 为 \(cur\) 节点的时间戳。

\(low[cur]\) 为 \(cur\) 节点的追溯值。

其中 \(low[cur]\) = \(min\){搜索树中 \(cur\) 的子树的节点的时间戳，子树中通过一条边，能够到达的节点的时间戳}

警告：分清 \(dfn\) 和 \(low\)！

无向图相关问题

桥与边双连通分量

桥

无向图中，如果割掉一条边，可以使整个无向图成为两个连通块，那么这条边成为割边或桥。

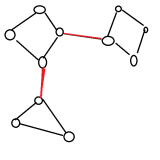
判定法则：

\[low[to] > dfn[cur] \]

显然，桥一定是搜索树上的边， 简单环中的边一定不是桥（P2607 [ZJOI2008]骑士中找环的方法之一）。

注意：不要用 \(cur\) 的 \(low/dfn\) 来更新 \(fa\) 的 \(low\)。但是可能会遇到重边等问题，所以记录入边编号 \(ine\)，防止遍历 \(ine\)！

求法：

//(initial)ecnt = 1
void tarjan(int cur, int ine) {
	dfn[cur] = low[cur] = ++dtot;
	for (register int i = head[cur]; i; i = e[i].nxt) {
		int to = e[i].to;
		if (!dfn[to]) {
			tarjan(to, i);
			low[cur] = min(low[cur], low[to]);
			if (low[to] > dfn[cur]) 
				iscut[i] = iscur[i ^ 1] = true;
		} else if (i != ine ^ 1)
			low[cur] = min(low[cur], dfn[to]);
	}
}

边双连通分量（e-DCC)

不存在割边的无向连通图为 边双连通图。极大边双连通子图为 边双连通分量。

一张无向连通图是边双连通图，当且仅当对于图中每条边，都在至少一个简单环上。

求法：

将桥删去后，整个图就成了一个个边双连通分量。

可以对图进行缩点。点内无桥，点间为桥。这样的话，缩点后没有任何环，是无向图森林。

void tarjan(int cur, int ine);
bool vis[N];
int siz[N];
int col[N], ctot;
void Dfs(int cur) {
	vis[cur] = true;
	col[cur] = ctot;
	siz[ctot]++;
	for (register int i = head[cur]; i; i = e[i].nxt) {
		int to = e[i].to;
		if (vis[to] || iscut[i])	continue;
		Dfs(to);
	}
}
vector<int> eg[N];
inline void adeg(int u, int v) {
	eg[u].push_back(v); eg[v].push_back(u);
}

//in main()
for (register int i = 1; i <= n; ++i) {
	if (!dfn[i])	tarjan(i, 0);
}
memset(vis, 0, sizeof(vis));
for (register int i = 1; i <= n; ++i) {
	if (!vis[i])	ctot++, Dfs(i);
}
for (register int i = 2; i <= ecnt; i += 2) {
	if (iscut[i]) {
		adeg(col[e[i].to], col[e[i ^ 1].to]);
	}
}

典型应用：无向图的必经边

必经边 = 割掉后点对不连通 = 点对间的割边（桥）

边双缩点+树剖，查询点对距离即可。

例题：【GDOI2015】水题

题意：

n 个点，m 条边， q 次询问，每次问 \(i\) 号边删去后会有多少点对互不可达。

n <= 1e5, m <= 1e6, q <= 8e5

发现不删也会有一堆点对互不可达（原本不一定联通）。如果删去的是割边，那么会增加其两端连通块的大小之积这么多的点对。

因此首先并查集搞出“初始答案”。然后 \(tarjan\) 求割边。然后将割边删去，进行缩点。此时缩好以后的图是一棵森林。因此我们可以对每棵树类似链剖的第一个dfs一样地搞出 \(dep\) 和 \(siz\)。没了。

注意区分“节点”与“节点”之间的关系。即区分：

森林--树（连通块）--树上的点（边双连通分量）--原图的点

割点与点双连通分量

割点

删去点及其所有连边后，原无向图分裂成为多个连通块，则这一点为割点。

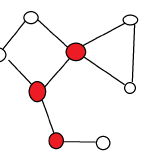
判定法则：

\[low[to] >= dfn[cur] \]

具体来说，对于（搜索树的）非根节点 \(cur\)，如果存在 \(low[to] >= dfn[cur]\)，那么 \(cur\) 为割点；对于根节点来说，如果有 至少两个 \(to\) 符合条件，那么根节点也为割点。

由于是 \(>=\)，因此就算拿 \(fa\) 的 \(dfn\) 来更新点的 \(low\)（显然不可能用 \(fa\) 的 \(low\) 来更新），也无法使该点跳出包围圈，不会将其 \(fa\) 误判为非割点。

求法：

模板提交处

void tarjan(int cur) {
	dfn[cur] = low[cur] = ++dcnt;
	int cnt = 0;
	for (register int i = head[cur]; i; i = e[i].nxt) {
		int to = e[i].to;
		if (!dfn[to]) {
			tarjan(to);
			low[cur] = min(low[cur], low[to]);
			if (low[to] >= dfn[cur]) {
				cnt++;
				if (!iscut[cur] && (cur != rt || cnt > 1))
					cut[++cuttot] = cur, iscut[cur] = true;
			}
		} else {
			low[cur] = min(low[cur], dfn[to]);
		}
	}
}

例题：P3469 [POI2008]BLO-Blockade

题意 : 给定一张无向联通图，求每个点被封锁（删去与该点相连的所有边）之后有多少个有序点对(x,y)(x!=y,1<=x,y<=n)满足x无法到达y

注意：没有删去那个点（不过都是细节了）

如果删去的不是割点，那么图仍然是联通图（除了单拎出来一个点），直接特判即可。

如果删去的是割点，那么图将会四分五裂。准确地说，如果对于这个点 \(cur\) 来说有 \(T\) 个 \(to\) 符合 \(low[to] >= dfn[cur]\) 的条件，那么这张图最多能分成 \(T + 2\) 个连通块，包括那么多 \(to\) 的子树 + \(cur\)节点 + 除此以外的所有点（这个可能没有）。

然后跑 \(tarjan\) 的时候记录一下 \(siz\)（搜索树的子树大小）。同时维护一下所有符合条件的子树大小之和（方便统计最后一部分对答案的贡献）。然后直接算每个点的答案就行了。

点双连通分量（v-DCC）

不存在割点的无向连通图为 点双连通图。极大点双连通子图为 点双连通分量。

一张图是点双连通图，当且仅当图的顶点数不超过2，或者图的任意两个点都在同一个简单环（圆圈）中。

证明：考虑点数至少为3的点双连通图。容易证明图的任意两个点都在同一个简单环中推出图时点双连通图，因此只需证明点双连通图的任意两个点都在同一个简单环中。

设两个点为 \(x,y\)。对 \(dis(x,y)\) 做归纳：当 \(dis(x,y)=1\) 时显然成立（否则 \(x\) 或 \(y\) 就是割点）对于 \(dis(x,y)=d\) 的情况，把最短路径拿出来，设 \(x\) 的下一个点是 \(z\)，则 \(z,y\) 在同一个简单环 C 上。而必然存在一条 \(x\) 到 C 的路径（否则 \(z\) 为割点)，设接到了 \(w\) 点，那么 \(x-w-y-z-x\) 就是一个简单环。

注意：一个割点可能同时属于多个 v-DCC！（非割点只属于一个）

求法

维护一个栈。无论是否是根，在遇到 \(low[to] >= dfn[cur]\) 时弹栈一直弹到 \(to\)，然后弹出的所有点再加上 \(cur\) 即为一个点双连通分量。

注意，不要一直弹到 cur 前面！否则会把 to 前面的一些不该弹的子树也弹掉

下面是一个反例：

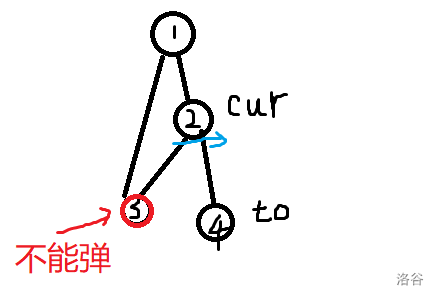
e-dcc 错误写法反例

- 缩点成树

比较麻烦的时缩点。有了一个个 v-DCC 后，就可以进行缩点。但是由于割点可能同时属于多个 v-DCC，因此我们要将割点复制一份作为中转节点。令人欣慰的时，缩点过后原图将成为一棵树（或森林）。如下图：

v-DCC

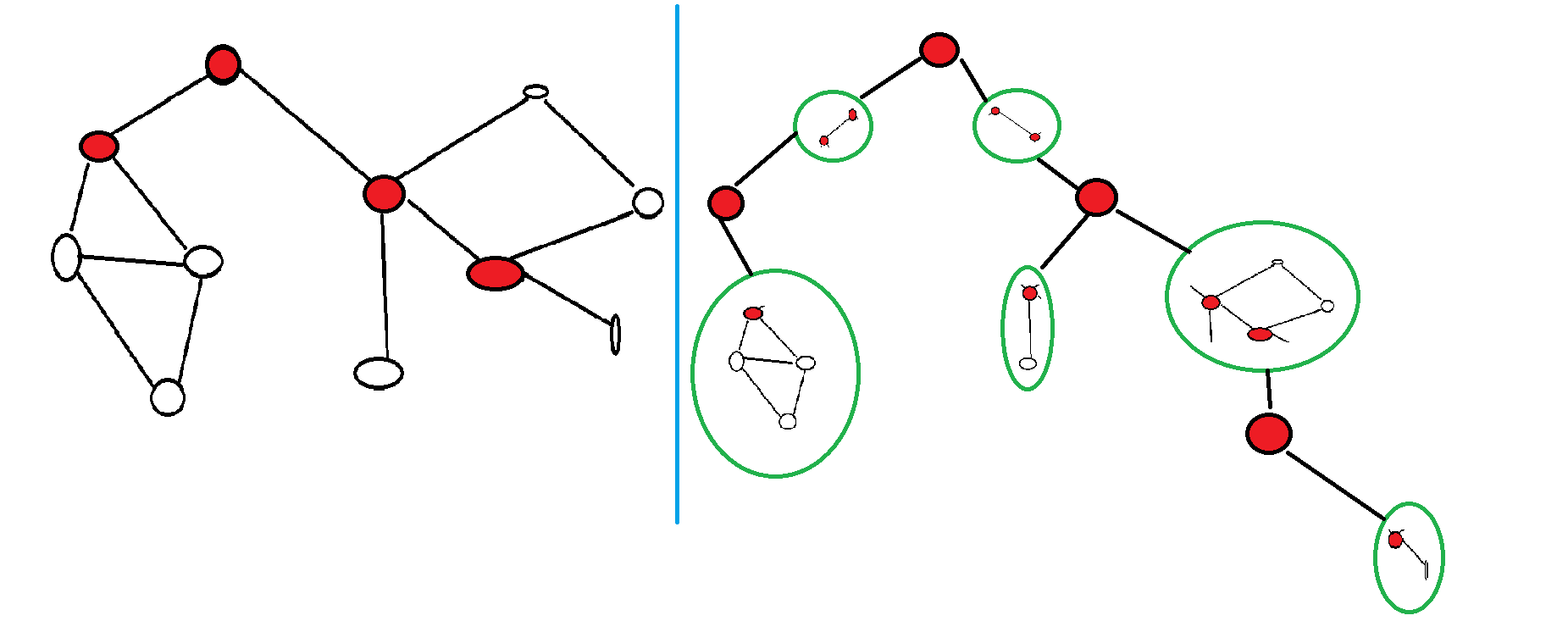
void tarjan(int cur) {
	stk[++stop] = cur; dfn[cur] = low[cur] = ++dcnt;
	int cnt = 0;
	for (register int i = head[cur]; i; i = e[i].nxt) {
		int to = e[i].to;
		if (!dfn[to]) {
			tarjan(to);
			low[cur] = min(low[cur], low[to]);
			if (low[to] >= dfn[cur]) {
				cnt++;
				if (cur != rt || cnt > 1)	iscut[cur] = true;
				int tmp; dcc_tot++;
				do {
					tmp = stk[stop--];
					dcc[dcc_tot].push_back(tmp);
				} while(tmp != to);
				dcc[dcc_tot].push_back(cur);
			}
		} else {
			low[cur] = min(low[cur], dfn[to]);
		}
	}
}

inline void rebuild() {
	int ntot = n;
	for (register int i = 1; i <= n; ++i) {
		if (iscut[i]) newid[i] = ++ntot;
	}
	for (register int i = 1; i <= dcc_tot; ++i) {
		for (register int j = 0; j < (int)dcc[i].size(); ++j) {
			int cur = dcc[i][j];
			if (iscut[cur]) {
				aded(nwid[cur], i); aded(i, nwid[cur]);
			} else {
				col[cur] = i;
			}
		}
	}
}

- 点双内部重建图

（做题Cycling City的时候遇到的问题）

有了上面的那个 dcc 数组，我们可以轻易地知道点双内部的点有哪些，但是不知道点双内部的边有哪些。显然，一条边只会属于一个点双。我们需要一个快速知道每条边在哪个点双中出现的算法。

\(O(n^2)\) 的做法：

对于一个点双，暴力枚举其中的点，然后枚举点的出边，判断端点是否在这个点双中。

一个菊花图就没了。

\(O(n \sqrt n \log n)\) 的做法：

用一个 set 或者哈希表维护每个点在哪些点双中。暴力枚举每一条边 \((u,v)\)，要求 \(u\) 在的点双数量小于 \(v\) 在的点双数量。暴力枚举 \(u\) 所在的所有点双，判断 \(v\) 是否也在其中。

复杂度证明类似三元环计数的证明。

如果用哈希表的话复杂度将降至 \(O(n \sqrt n)\)，有一个大常数。

\(O(n)\) 的做法：

tarjan 函数内部维护点的栈的同时维护一个边的栈，将所有遍历到的边（即使没有走）都加入，弹点的栈的同时再弹一波边的栈即可。最后还要判断一下边到底是否属于这个点双，以及对边进行去重。

一个点双内的边至少被该点双找到一次，我们只能保证这个了。可能会存在一个点的儿子能到达这个点的另一个儿子的情况，这时可能会出一些奇怪的情况。

void tarjan(int cur, int ine) {
	low[cur] = dfn[cur] = ++dcnt;
	stk[++stop] = cur;
	for (int i = head[cur]; i; i = e[i].nxt) if (ine != (i ^ 1)) {
		int to = e[i].to; estk[++etop] = i;
		if (!dfn[to]) {
			tarjan(to, i);
			MIN(low[cur], low[to]);
			if (low[to] >= dfn[cur]) {
				int tmp; ++dcctot;
				do {
					tmp = stk[stop--];
					dcc[dcctot].push_back(tmp);
				} while (tmp != to);//bug
				dcc[dcctot].push_back(cur);
				do {
					tmp = estk[etop--];//Bug
					dcce[dcctot].push_back(tmp);
				} while (tmp != i);
			}
		} else MIN(low[cur], dfn[to]);
	}
}
...
int main() {
	...
	for (int i = 1; i <= n; ++i) if (!dfn[i])	tarjan(i, 0);
	for (int i = 1; i <= dcctot; ++i) {
		for (unsigned int j = 0; j < dcc[i].size(); ++j) {
			int cur = dcc[i][j]; nvis[cur] = true;
		}
		for (unsigned int j = 0; j < dcce[i].size(); ++j) {
			int jzp = dcce[i][j];
			int u = e[jzp].to, v = e[jzp ^ 1].to;
			if (nvis[u] && nvis[v] && !evis[jzp >> 1])
				aded(u, v), aded(v, u), evis[jzp >> 1] = true;
		}
        ...
		for (unsigned int j = 0; j < dcc[i].size(); ++j) {
			int cur = dcc[i][j];
			ve[cur].clear();
			nvis[cur] = false;
		}
	}
    ...
}

典型应用：无向图必经点

例题：P4320 道路相遇

必经点 = 删去这个点后点对不连通 = 点双缩点后的树上路径的割点树

需要完整地建出缩点后的树。为了防止边混淆，在建立缩点后的树之前先将原图的边清空。

注意对于路径端点（即点对）需要特判。

（题解里面好多说圆方树的，不知道是不是和tarjan做法有关）

\(Code:\)my record

习题：UVA1464 Traffic Real Time Query System

例题：SP2878 KNIGHTS - Knights of the Round Table

题意：求无向图中不属于任何奇环的节点数量。其中1个点不算环。

首先我们最好把一个个环（不一定是简单环）都提出来。这个要用点双连通分量。因为边双连通分量不好搞定 \(∞\) 形状的情况。我们要求每个“块”内的任意两点都属于至少同一个环。（毕竟是点在环上的问题，而不是边在环上的问题）

可以证明，对于每一个块（v-DCC)，如果包含有至少一个奇环，那么块内的所有点都在至少一个奇环上。（找到奇环后，由于要求任意两个点都在至少同一个环上，因此奇环外的点一定会与奇环上的点以环的形式连接，出现环套环的现象。因此那一个环有两种形态，必定是一种奇环一种偶环）。

于是黑白染色即可。由于割点在不同的DCC上，因此每次染色前需要重置“颜色”。

小于等于两个点的DCC恰好也符合，正好不用特判。

代码:my record

类似的题：UVA1464 Traffic Real Time Query System（这道题建议阅读英文题面）

提示：对于无向图边对的必经点数，为四对点的必经点数的最大值。通过找规律可以得到。严谨证明应该也不难，就在缩点后的数上讨论各种（两种）情况即可。

代码：my record

习题

P3225 [HNOI2012]矿场搭建

P2860 [USACO06JAN]Redundant Paths G

有向图相关问题

tarjan 算法、强连通分量与缩点

有向图的 tarjan 已经很熟悉了。

注意1：如果 \(to\) 不在栈中，就不要用它更新 \(cur\) 的 \(low\) 了。

注意2：将 \(tmp\) 弹栈时，要 \(vis[tmp] = false\) ！

\(Code:\)

void tarjan(int cur) {
	dfn[cur] = low[cur] = ++dcnt;
	stk[++stop] = cur; vis[cur] = true;
	for (register int i = head[cur]; i; i = e[i].nxt) {
		int to = e[i].to;
		if (!dfn[to]) {
			tarjan(to);
			low[cur] = min(low[cur], low[to]);
		} else if (vis[to]) {
			low[cur] = min(low[cur], low[to]);
		}
	}
	if (low[cur] == dfn[cur]) {
		int tmp; ctot++;
		do {
			tmp = stk[stop--];
			col[tmp] = ctot;
			vis[tmp] = false;
		} while (tmp != cur);
	}
}

有向图的必经边与必经点

似乎和支配树有关？这里只有DAG的必经边和必经点。

从 \(S\) 出发沿正向边（即原图的边）拓扑dp求出 \(fs[cur]\) 表示 \(S\) 到 \(cur\) 的方案数；从 \(T\) 出发沿反向边（即原图的反向边）拓扑dp求出 \(ft[cur]\) 表示 \(cur\) 到 \(T\) 的方案数。这样， \(fs[T]\) 即为总方案数。

如果有一条边\((u, v)\)，满足：\(fs[u] * ft[v] == fs[T]\)，即为必经点；

如果有一个点 \(cur\)，满足：\(fs[cur] * ft[cur] == fs[T]\)，即为必经点。

由于方案数可能很大，需要进行Hash！

注意：

一般图的连通性的题目要对DCC/SCC为一的情况进行特判。
求点双和求SCC的写法不太一样，求点双是 do { } while (tmp != to); 一直到把 \(to\) 弹出去为止（最好写成 do-while 形式，否则容易忘记弹 \(to\)，SCC同理）；而求SCC则是 do { } while (tmp != cur); 要把自己弹出去。
点双可以用来水过很多圆方树的题，比如道路相遇，以及战略游戏。

附：

tarjan 求割边及缩点（调试用）

//(initial)ecnt = 1
void tarjan(int cur, int ine) {
    dfn[cur] = low[cur] = ++dtot;
    for (register int i = head[cur]; i; i = e[i].nxt) {
        int to = e[i].to;
        if (!dfn[to]) {
            tarjan(to, i);
            low[cur] = min(low[cur], low[to]);
            if (low[to] > dfn[cur]) 
                iscut[i] = iscur[i ^ 1] = true;
        } else if (i != ine ^ 1)
            low[cur] = min(low[cur], dfn[to]);
    }
}
bool vis[N];
int siz[N];
int col[N], ctot;
void Dfs(int cur) {
	vis[cur] = true;
	col[cur] = ctot;
	siz[ctot]++;
	for (register int i = head[cur]; i; i = e[i].nxt) {
		int to = e[i].to;
		if (vis[to] || iscut[i])	continue;
		Dfs(to);
	}
}
vector<int> eg[N];
inline void adeg(int u, int v) {
	eg[u].push_back(v); eg[v].push_back(u);
}

//in main()
for (register int i = 1; i <= n; ++i) {
	if (!dfn[i])	tarjan(i, 0);
}
memset(vis, 0, sizeof(vis));
for (register int i = 1; i <= n; ++i) {
	if (!vis[i])	ctot++, Dfs(i);
}
for (register int i = 2; i <= ecnt; i += 2) {
	if (iscut[i]) {
		adeg(col[e[i].to], col[e[i ^ 1].to]);
	}
}

tarjan 求割点及缩点（调试用）

void tarjan(int cur) {
    stk[++stop] = cur; dfn[cur] = low[cur] = ++dcnt;
    int cnt = 0;
    for (register int i = head[cur]; i; i = e[i].nxt) {
        int to = e[i].to;
        if (!dfn[to]) {
            tarjan(to);
            low[cur] = min(low[cur], low[to]);
            if (low[to] >= dfn[cur]) {
                cnt++;
                if (cur != rt || cnt > 1)   iscut[cur] = true;
                int tmp; dcc_tot++;
                do {
                    tmp = stk[stop--];
                    dcc[dcc_tot].push_back(tmp);
                } while(tmp != to);
                dcc[dcc_tot].push_back(cur);
            }
        } else {
            low[cur] = min(low[cur], dfn[to]);
        }
    }
}

inline void rebuild() {
    int ntot = n;
    for (register int i = 1; i <= n; ++i) {
        if (iscut[i]) newid[i] = ++ntot;
    }
    for (register int i = 1; i <= dcc_tot; ++i) {
        for (register int j = 0; j < (int)dcc[i].size(); ++j) {
            int cur = dcc[i][j];
            if (iscut[cur]) {
                aded(nwid[cur], i); aded(i, nwid[cur]);
            } else {
                col[cur] = i;
            }
        }
    }
}

tarjan 求强连通分量（调试用）

void tarjan(int cur) {
    dfn[cur] = low[cur] = ++dcnt;
    stk[++stop] = cur; vis[cur] = true;
    for (register int i = head[cur]; i; i = e[i].nxt) {
        int to = e[i].to;
        if (!dfn[to]) {
            tarjan(to);
            low[cur] = min(low[cur], low[to]);
        } else if (vis[to]) {
            low[cur] = min(low[cur], low[to]);
        }
    }
    if (low[cur] == dfn[cur]) {
        int tmp; ctot++;
        do {
            tmp = stk[stop--];
            col[tmp] = ctot;
            vis[tmp] = false;
        } while (tmp != cur);
    }
}

posted @ 2020-07-24 18:52 JiaZP 阅读(359) 评论(1) 编辑收藏举报

刷新页面返回顶部

JiaZP