P3756 [CQOI2017]老C的方块
看到网格图+最优化问题,当然要想黑白染色搞网络流。不过这道题显然无法用黑白染色搞定。
仔细观察那四种图形,发现都是蓝线两边一定有两个格子,两个格子旁边一定还有且仅有一个格子。因此我们可以这么染色:
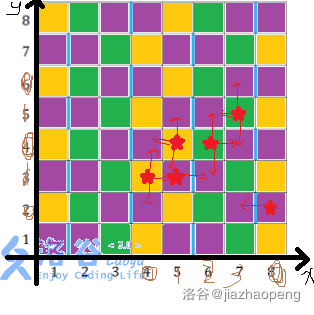
(图片有点丑)
染完色以后直接三分图匹配求最小割即可。
可以看出,横着4个一循环,纵向2个一循环,所以一共有8中不同的格子。实际上,我们只需要在那六个星星的位置进行判断即可。
关键代码:(S -> 黄 -> 紫 -> 绿 -> T)
for (register int i = 1; i <= n; ++i) {
read(X[i]), read(Y[i]), read(W[i]);
mp[X[i]][Y[i]] = i;
}
for (register int i = 1; i <= n; ++i) {
int x = X[i], y = Y[i];
int mx = x & 3, my = y & 1;
if (mx == 1 && my == 1) {//purple
int you = mp[x + 1][y];
add(i, you, min(W[i], W[you]));
} else if (mx == 0 && my == 0) {//purple
int zuo = mp[x - 1][y];
add(i, zuo, min(W[i], W[zuo]));
} else if (mx == 0 && my == 1) {//yellow
add(s, i, W[i]);
int shang = mp[x][y + 1];
add(i, shang, inf);
int xia = mp[x][y - 1];
add(i, xia, inf);
int you = mp[x + 1][y];
add(i, you, inf);
} else if (mx == 1 && my == 0) {//yellow
add(s, i, W[i]);
int shang = mp[x][y + 1];
add(i, shang, inf);
int xia = mp[x][y - 1];
add(i, xia, inf);
int zuo = mp[x - 1][y];
add(i, zuo, inf);
} else if (mx == 2 && my == 0) {//green
add(i, t, W[i]);
int shang = mp[x][y + 1];
add(shang, i, inf);
int xia = mp[x][y - 1];
add(xia, i, inf);
int you = mp[x + 1][y];
add(you, i, inf);
} else if (mx == 3 && my == 1) {//green
add(i, t, W[i]);
int shang = mp[x][y + 1];
add(shang, i, inf);
int xia = mp[x][y - 1];
add(xia, i, inf);
int zuo = mp[x - 1][y];
add(zuo, i, inf);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号