最小割&网络流应用

重要链接

基础部分链接 ： 二分图 & 网络流初步

zzz大佬博客链接 ： 网络流学习笔记

重点内容：最小割二元关系新解(lyd's ppt)

题目：网络流相关题目

lyd神犇课件链接 ： 网络流模型设计lyd（提取码：m5sd）

国家集训队2007胡伯涛论文 ： 算法合集之《最小割模型在信息学竞赛中的应用》

最详细（也可能现在不是了）网络流建模基础

对于网络流的基础部分以及其在二分图方面的应用，详见上面的第一个链接。

先 Copy 下重点：

最小割

最大流等于最小割。

如何找到最小割的割边？

  1. 从S开始沿着残量网络BFS，把能到达的点标记上。

  2. 连接已标记的点和未标记的点的正向边为该网络的一个最小割集。（-by lyd大佬）

如何找最小割的必须边？

  1. 从S开始BFS跑残量网络。

  2. 从T开始反向BFS跑残量网络。

  3. 枚举从S指向T的满流边，这些边即为必须边

如何找某种情况的最小割的可行边？

  1. 满流

  2. 删掉后找不到u -> v的路径

于是：残余网络中tarjan跑SCC, (u, v)的u, v都在同一SCC中说明存在残量网络u -> v的路径 -by lyd大佬

网络流常用思想：点边转化思想

拆点：

把点拆成入点和出点，两点间边权为点权。或者拆成有两个特殊含义的点。

拆边：

对于边权比较复杂的问题（比如和第几种情况、之前选用该点次数等有关，但不管怎样都会选最小的情况作为代价），把所有情况分解成某几条边上的权值和。（类似于二进制拆分多重背包？）

如: #6068. 「2017 山东一轮集训 Day4」棋盘 ；还有P4307 [JSOI2009]球队收益 / 球队预算

注意！

  • dinic的弧优化记得加，记得初始化！！别忘了s、t的初始化！！+1

  • 一定要连反向边！！！！！

  • 费用流注意一下 \(vis\) 的适用情况

以上为开头链接部分内容。

以下为正文。

Part 1

网络流模型设计lyd（提取码：m5sd）

（从第八页开始，前七页在前面有说过）

动态加点

例题：P2050 [NOI2012]美食节

题意 ： n 个菜，每个菜有 \(p_i\) 个人（互不相同）选； \(m\) 位厨师， \(j\) 厨师做 \(i\) 菜的时间为 \(t_{i, j}\)。求最小等待总时间。

\(n <= 40; m <= 100; \sum p <= 800\)

建议先做一下简化版：P2053 [SCOI2007]修车

利用费用提前计算等思想，我们发现 \(j\) 厨师对答案的贡献是： \(\sum{i * t[x_i][j]}\)，其中 \(x_i\) 为交付给 \(j\) 厨师的第 \(i\) 个人选择的菜。

然后我们的思路是把每个厨师拆成 \(\sum p_i\) 个点，代表每个厨师要做的（倒数）第 \(i\) 个菜的相关费用。（这样费用便于计算），然后再搞一搞，用最小费用最大流跑一跑。

然后复杂度会炸掉。

我们发现肯定不会每个厨师都做 \(\sum p_i\) 道菜，直观的想法是，谁做菜快（受到众人的青睐）就多给他一些机会。

具体来说，就是动态加点。先按照最小费用（第一次的最短路）跑他一跑，发现谁备受青睐（都选他，即他连向汇点的边都满流），就给他再开一个做饭的位置，给他多做一道菜的机会。然后重复。最后一直跑到最大流为 \(\sum p_i\) 为止（所有菜都做完了）。

\(Code:\)my record

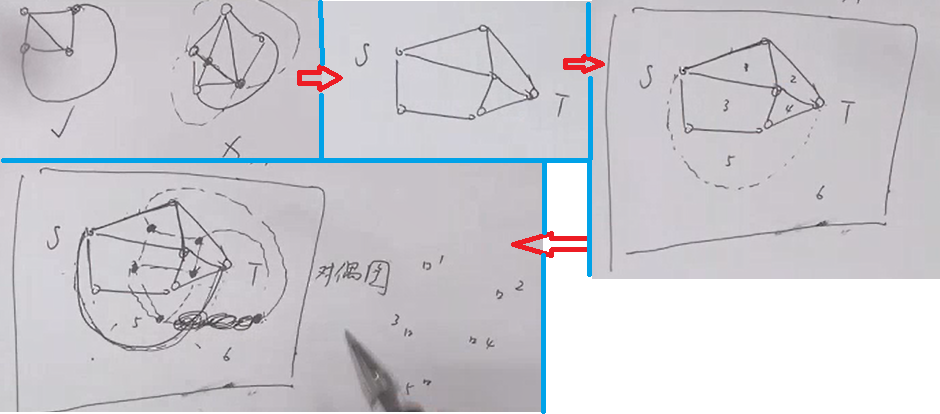
平面图与对偶图

经典例题 ： P4001 [ICPC-Beijing 2006]狼抓兔子

平面图 ：

一张无向网络，能够在一张纸上画出来，并且边不交叉。

网格图是特殊的平面图。

一张平面图的对偶图

将平面图在纸上画出来，并且将源点与汇点用另外一条边相连。发现一张纸被平面图的边分成了好几部分。将这几部分用带编号的点来表示，原图的边（不含后来加的源点到汇点的边）转化成其两侧的区域点的连边。

平面图的最小割 等于 其对偶图的最短路

跑从对偶图中的 \(S'\) -> \(T'\)的路径，发现每条路径都将原网络分割成两部分（即源汇分开），是一种割。因此平面图的最小割 = 对偶图的最短路。

平面图对偶图

这样，\(O(n^2m)\)（假）就有望优化成 \(O(nlogn)\)（\(dijkstra\))。

\(Code:\)my record

加强 : 有向网格图的平面图与对偶图

例题：P2046 [NOI2010]海拔

这回我们每条边有了两个不同的权值。其实和之前差不多，只不过当时我们理直气壮地把每条边直接当作两条边处理，这回我们要区别这两条边了。

通过画图可知，对于网格图的对偶图来说，（原图中）从坐上走到右下的最小割，就相当于（对偶图中）从坐下走到右上。那么我们直接把所有（原图的）边都逆时针旋转 \(90\) °，就是对偶图上的边。

具体来说，原图中的每条边，就相当于（对偶图中）从它的右侧穿越到它的左侧。据此建图即可。

如果有些边根本就没有呢？那么就说明这些边不用花费任何代价就可以被割断，设置一些流量为0 的边即可。

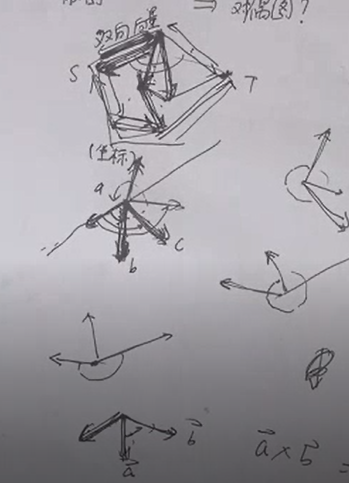
拓展 ： 给出平面图，求对偶图

最小左转法

给出平面图上的一些点的坐标，还有连接其中某些点的边（含边权），求其对偶图。

关键在于求出所有小区域，需要高超的计算几何技巧。

（直接Copy）

原图中的每条线段看做双向向量。
• ① 任选一条未被标记的向量u→v。
• ② 找到与向量v→u逆(或顺)时针方向夹角最小的向量v→w。
• ③ 如果v→w已被标记，转到④；否则将它标记，令v=w, u=v，重复②。
• ④ 重复①~③，直至所有向量都被标记。
• 每次到达④，都会找到一个区域。通过记录每个区域的边，计算它的面
积正负，可以判断它是内部区域，还是外部的无限大区域。


• 如何求与向量v→u逆时针方向夹角最小的向量？
• 两种需要更新答案v→p的情况：
• v→p在v→u的顺时针方向（vu × vp<0）
并且v→w在v→u的逆时针方向（vu × vw>0）
• v→p和v→w在v→u同侧
并且v→w在v→p的顺时针方向（vp × vw<0）

计算几何对偶图

例题：

P3249 [HNOI2016]矿区

建对偶图 + 生成树

#2965. 保护古迹

点被围起来 = 点不与最外面联通

因此建立对偶图，暴力枚举点集，求最小割。

多源点最小割？超级源点！

#2960. 跨平面

建对偶图 + （无根）最小树形图。

不错的计算几何题。

最大权闭合子图

一张有向无环图，点有点权（可能为负），对于边 \((u, v)\)，如果选择 \(u\) ，就必须选择 \(v\)。求所选的点的最大权值和。

方法

对于所有点权为正的点 \(u\)，我们连\((s, u, val[u])\)；对于点权为负的点 \(v\)，我们连 \((v, t, -val[v])\)；对于边 \((u, v)\)，我们连 \((u, v, inf)\)。求最小割，正点权和减去最小割即为答案。

对于环，需要特殊处理（如缩点等等）。

理解与证明

首先我们先选上所有正点权。为了满足边的要求，我们要选择一些负点权，或者抛弃一些正点权。

建好图后，如果我们割掉正点和 \(S\) 之间的边，而把正点权归为 \(T\) 那边，则说明我们放弃了正点；如果我们割掉负点和 \(T\) 之间的边，而把负点归到 \(S\) 那边，说明我们要选择这个负点。

因此，方案为 ： 从 \(S\) 开始 \(dfs\)，标记能经过的点。这些能经过的点即为我们选择的点。

最大密度子图

一张无向图，点有点权，边有边权。选出其中的一个子图，使得 点权之和与边权之和的比值最小（即 边权和与点权和的比值最大）。输出点权之和与边权之和的比值。

前置技能：01分数规划

二分点权与边权的比值为 \(d\)。那么我们的任务是最小化 \(\sum_{p}val_p - d * \sum_eval_e\)，查看是否为正。

如果我们把每条边看作一个点，那么我们选择这条边就要获得 \(- d * val_e\) 的代价（点权）；选择一个（原图）点，就要获得 \(val_p\) 的代价（点权）。并且要求选择边就一定要选择边两边的点。

然后成功转化为最大（小）权闭合子图的问题。

复杂度：约\(O((n + m)^3)\)。

算法改进

我们希望尽量少的让复杂度与 \(m\) 相关。

考虑二分后最后选出的那个子图（子图上的点记作黑点），如果我们知道子图的点是哪些，那么我们一定会选出黑点与黑点相连的所有边。这些边与子图上的点称之为诱导子图。答案为：

\[ans = \sum{val_p} - d * \sum{val_e} \]

\[= \sum_p{val_p} - \frac{d}{2} * ({\sum_{(p, q), p~is~black}{val_{p, q}}} - \sum_{(p, q), p~is~black, q~is~wight}val_{p, q}) \]

其中中间的那个求和式我们可以预处理出来，成为与点权有关的式子，记之为 \(sum[p]\)；最右面的那个求和式即为最小割。

我们将所有点与 \(S\) 连边\((S, p, val[p] - d / 2 * sum[p])\)，(原图中的）边连为双向边 \((u, v, 1 / 2 * val_{u, v})\)，然后求最小割得:\(mincut\)

至于如何处理负数流量，以及如何处理分数，下面“最小割二元关系新解”部分会有讲解。

答案即为 \(mincut\)。

方案：某点如果与 \(S\) 的连边为割边，则该点被选。

Continued...

混合图欧拉回路

一张图中既有无向边，也有有向边，求是否有经过每条边恰好一次的回路。

（无向图欧拉回路、有向图欧拉回路可以通过度数（或入度、出度关系)来直接判断。）

混合图欧拉回路可以变成：是否存在一种无向边定向方案，使得每个点的入度等于出度。

如果我们先把无向图随意定向，那么会出现某些点入度出度不等的情况。（当然，如果某个点的出入度之和为奇数，则一定无方案）但是，我们可以通过对一些无向边的方向进行反悔，来修改每个点的出入度关系。

一条无向边被定为(u -> v)，它有机会改成(v -> u)，使得 u 的出入度之差减二， v 的出入度之差加二。

因此我们设 \(D[cur] = \frac{ind[cur] - outd[cur]}{2}\)，并且先将无向边 \((u, v)\) “连”（原图中)成 \((u -> v)\)，并且连一条反悔边 \((v -> u, val = 1)\)，表示反悔将使 \(D[u]--,D[v]++\)。有向边按题意连，同时维护 \(D\)。最终如果 \(D\) 出现小数，说明无合法方案；否则 \(S ->\) 正数 \(D\)，负数 \(D -> T\)（不难，好好想想）。

然后跑最大流。如果可以满流（最大流等于所有正数节点的权值之和），那么说明至少存在一种方案，能够使得该图为欧拉回路。

实际上最快的理解方式就是举个简单的例子，寻找正确的方法。

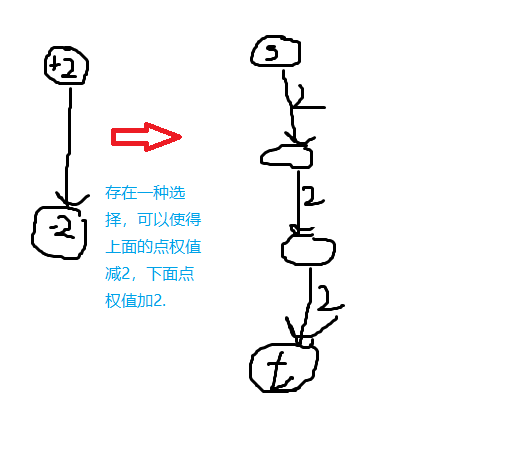
混合图欧拉回路

无源汇有上下界可行流

rt

首先把下界强行跑满，但是可能会不符合网络流的流量守恒的性质。

根据入与出的差值，如果某个点入过多，那么就给它找个出的机会，就是来自 \(S\) 的帮助；反之，如果出过多，就给它找到个入的机会，就是来自 \(T\) 的帮助。

因此，我们将入过多的点与 \(S\) 相连，出过多的点与 \(T\) 相连，剩余的边的边权为原图的 \(max - min\)。然后跑最大流，能满流就说明可行。

可行的方案为跑完最大流后的（除去 \(S\) 和 \(T\)）网络（加上下届）。

无源汇有上下界最小费用可行流

例题： P3980 [NOI2008]志愿者招募

由于下界是必须选的，因此下界必须的费用是一定会对答案造成贡献的。剩下的对答案的贡献为 ： 为了流量守恒，不得不流动的流量，出现在最后的跑最大流中。因此最后我们在连向 \(S\) 或 \(T\) 时，将边费用设置为 0.然后跑最小费用最大流，最后两部分总和即为答案。

最小/大费用循环流

例题1：UVA1659 帮助小罗拉 Help Little Laura

例题2：T134939 Tree

这里的循环流指的是：无源汇，容量无下界有上界，边有费用，需要满足流量守恒。求一股循环流满足以上条件，且费用最小。

还是常见的套路（以最小费用最大流为例）：首先把负边权给强制选上（为了更优，同时避免负环），不过注意要留“后路”，即返回边。这样的话虽然费用尽可能的少了，但是“流量守恒”可能就不符合了。于是我们可以利用S和T调节一下，使得流量守恒，又要尽可能少地花费。这一步就是普通的MCMF了。

即：正边 \((u, v, w, f)\) 照常连，负边\((u, v, w, f)\) 先让答案加上个\(w * f\)，然后连边：\((u, t, w, 0), (s, v, w, 0), (v, u, w, -f)\)，跑最小费用最大流。最终答案就是一开始加的那些\(w * f\) 再加上后来跑的最小费用。

有源汇有上下界可行流

rt

实际上这个更常考些， 如: Budget 和 Shoot the Bullet

有源汇的网络流，源汇可以不满足流量守恒，源点可以随便流出，汇点可以随便流入。于是我们将其连边（ \(T\) -> \(S\)），上下界设置为 \([0, +∞]\)。然后就是无源汇有上下界网络流。

有源汇有上下界最大流/最小流

其实都可以用二分来做。

最大流 ： 求完可行流后，从\(s\)（原源点） 到 \(t\) （原汇点）求一遍最大流（只经过原图的点，跑余量网络），\(ans += mxflow\)。

最小流 ： 求完可行流后，从\(t\)（原汇点） 到 \(s\) （原源点）求一遍最大流（只经过原图的点，跑余量网络）， \(ans -= mxflow\)。（lyd说填充循环流，并不太懂）

有源汇有上下界最小流还有一种更简洁的方法：可以先不 \(t\) -> \(s\)，跑一个“无源汇”有上下界可行流，这时候所有循环流都已经填满，然后我们再 \(t\) -> \(s\)，再跑一遍“无源汇”有上下界可行流，这时 \(t\) -> \(s\) 的流就是不得不跑的最小流

有源汇有上下界最小费用可行流

基本上所有的“最小费用”都是将 bfs 改成 spfa，在费用最小的前提下达到限制条件。

例题：#2226. 「AHOI2014」支线剧情

习题

P3980 [NOI2008]志愿者招募

P4553 80人环游世界

最小割二元关系新解

见链接。

模拟费用流

序列

给俩长为 \(n\) 的序列，要求每个序列选择恰好 \(K\) 个下标，且至少有 \(L\) 个下标同时被选。求选择的数的和的最大值。\(1 \le L \le K \le n \le 10^6\)

感谢 i207M 学长的帮助。应该是我第一次弄懂模拟费用流吧。

首先可以建图：

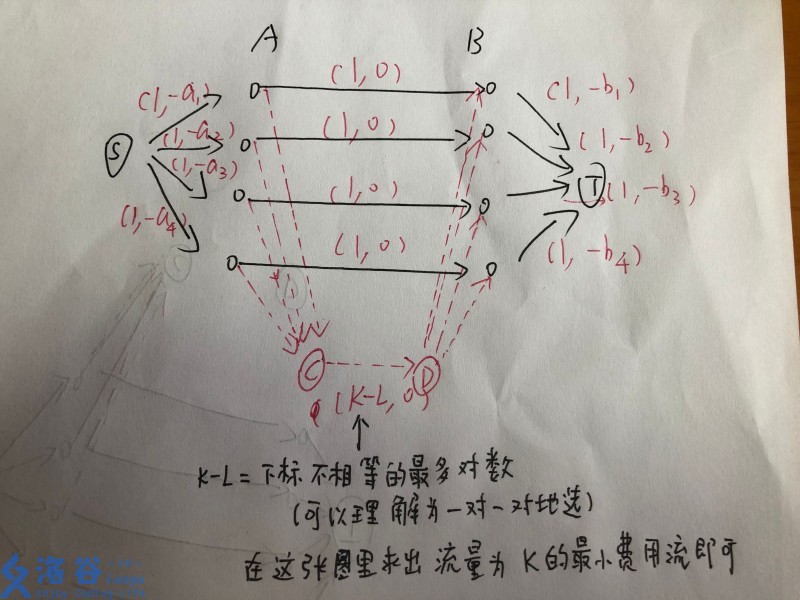
序列网络流

跑流量为 \(K\) 的最小费用流。

参考题解，我们可以先给 CD 跑满 K 的流量，然后想办法退掉 L 的流量，跑到中间的那些 \((1,0)\) 的边中。

讨论如何退流：

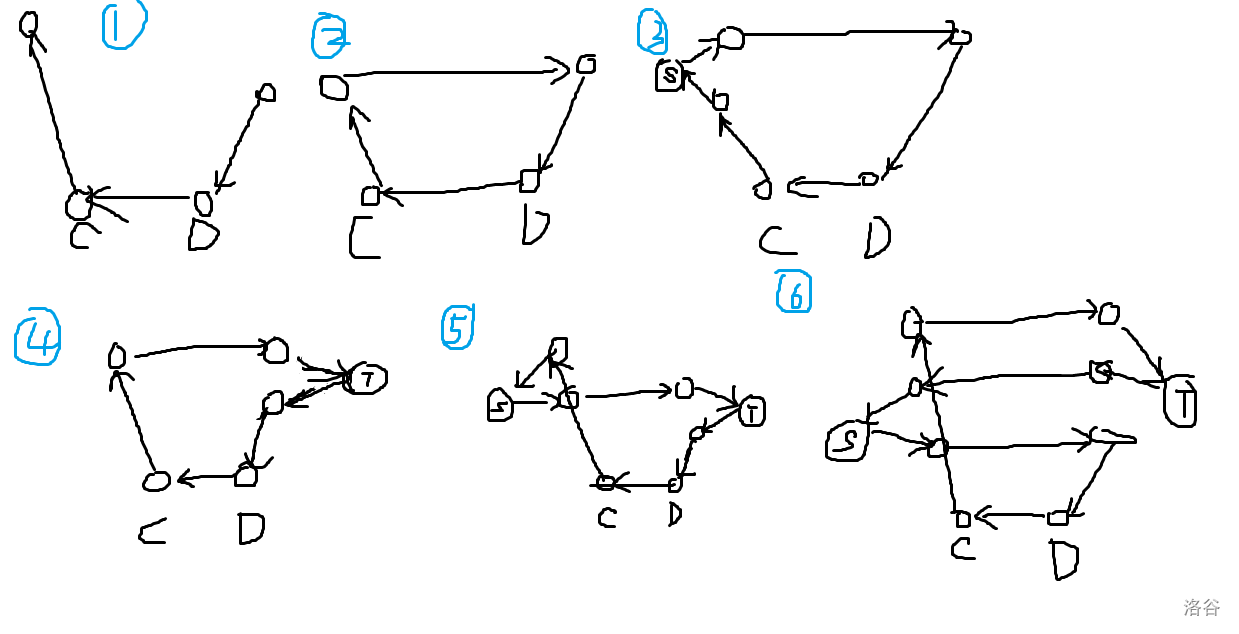
先不考虑退中间 \((1,0)\) 边的流。首先肯定长成 ① 的样子，直接连起来就是 ②，去 \(S\) 逛一圈就是 ③，去 \(T\) 逛一圈就是 ④，都逛一圈就是 ⑤。由于一条增广路不会经过重点，不会经过两次 \(S\) 或 \(T\)，于是这四种情况基本上就全了。

考虑上退中间边的流的情况。手玩一下发现就只有 ⑥ 这一种情况，其余就重复经过 \(S\) 或 \(T\) 了。

维护好每一对点的状态，模拟即可。（②可以提前处理好，因为以后不会生成②）

序列模拟费用流

Part 2

国家集训队2007论文集7.胡伯涛《最小割模型

还是直接看论文吧（尽管看不懂）

满流边不一定是最小割！！

mincut

基于定义的直接应用

例题：网络战争

题意：给一张无向图，边有边权，有源点 \(S\) 和汇点 \(T\)。最小化：

\[\frac{\sum_{e}w_e}{|C|} \]

其中 \(C\) 为使 \(S\) 与 \(T\) 分开的割集， \(e\) 为割集中的边。

直接除法不是很好做。发现答案具有单调性。我们可以二分答案 \(d\)，然后 \(che()\) 函数就是要判断：

\[\frac{\sum_{e}w_e}{|C|} >= d \]

即

\[\sum_{e = (u, v)}{w_e - d} >= 0 \]

然后以新边权为容量，求最小割即可。

容量为负？那选他一定更优（管他在不在割集里面），直接把它割掉（即不加这条边或设置其容量为0）统计答案。剩下的正权边再跑最小割。

例题 ： SP839 OPTM - Optimal Marks

版本二提交处：bzoj2400

题意：

给你一个无向图G（V，E）。 每个顶点都有一个int范围内的整数的标记。 不同的顶点可能有相同的标记。

对于边（u，v），我们定义:

\[Cost(u, v)\ = mark[u] \ xor \ mark [v] \]

现在我们知道某些节点的标记了。你需要确定其他节点的标记，以使边的总成本尽可能小。在此条件下，要求点的标记总和尽可能小。 在这两个条件下，你可以输出任意一种合法的方案，以及边的总成本和最小的点权和。

自己想出来的为数不多的最小割题，尽管TLE and WA 调到飞天。。。

发现 \(xor\)，并且各位之间互不干扰，因此可以针对每一个二进制位做。

然后有点像“最大权闭合子图”？总之就是未知的点选一或者选0，要求最终边权和最小。

发现从已知的 1 走到 0，期间至少要经过一条对答案有贡献的边。或者说，我们要将点集分成两类“块”，1和0属于不同的“块”内。我们要做的是选出一些点，使得“1块”和“0块”不连通，并要求“边界”最少。然后就很像最小割了。

将 \(S\) 向 "1点"连 inf 边， "0点" 向 \(T\) 连 inf 边，原图中的边为 1 边。求最小割。然后从 \(S\) 出发dfs，遍历到的点为我们选择的 1 点。

为什么这样做点权和最小呢 ？

点权和可以拆成每一位对答案的贡献。要求我们在做每一位时，点权和一定最小，也就是说，希望dfs到尽可能少的点。因为我们总是一遇到满流边就停止了，因此我们走到的是 \(S\) 所在的“最小区域”。

举个例子：

S --(inf)--> 1 --(1)--> 2 --(1)--> 3 --(1)--> 4 --(1)--> 5 --(inf)--> T

这张图你随便认为最小割是哪一个，反正我们从 \(S\) 出发，只走到了 1。

Continued...

一些（许多）例题+习题

posted @ 2020-07-21 14:09  JiaZP  阅读(537)  评论(0)  编辑  收藏  举报