回文树（回文自动机）（PAM）

第一个能看懂的论文：国家集训队2017论文集

这是我第一个自己理解的自动机（AC自动机不懂KMP硬背，SAM看不懂一堆引理定理硬背）

参考文献：2017国家集训队论文集 回文树及其应用 翁文涛

参考博客：回文树

一些定义

• （回文）子串不包括空串。

• （回文）后缀不包括原串本身，如果找不到，就是空串。

• 定义 \(len[cur]\) 为 \(cur\) 节点的代表串长度，\(son[p][c]\) 表示一条转移路径，\(fail\) 表示失配指针。

• 定义 \(\Sigma\) 为字符集大小。

• \(c\) 通常表示字符，\(s\) 或者 \(S\) 通常代表字符串，\(p,cur\) 代表节点。

• 有时我可能会将“回文串”和“回文树上代表其的节点”混用。

回文树原理及构造

回文树的结构

回文树由两棵树组成，一棵奇树，一棵偶树。
每个节点代表恰好一个回文串，每个原串的回文子串恰好有一个对应节点。
奇树上的点长度都为奇数，偶树上的点长度都为偶数。特别地，奇树根节点（通常编号为1）的长度为 -1，偶树根节点（通常编号为0）的长度为 0.
每个点都有一个 \(fail\) 指针，指向当前串的最长回文后缀。众多 \(fail\) 构成一棵以 1 为根的 \(fail\) 树，其中父亲为儿子的最长回文后缀；满足 \(len[fa] < len[son]\)；并且一个回文串的所有回文后缀为从该节点到根节点 1 所经过的链上 \(len\) 为正数的回文串。

节点数和转移（边）数

可以证明，一个字符串的本质不同的回文子串数量不超过字符串长度，因此回文树节点数为 \(O(|s|)\)。证明如下:

考虑新加入一个字符 \(c\) 所新增的位置不同的回文子串：\(s[l_1, n], s[l_2, n], ...\)，那么除了 \(s[l_1, n]\) 外，其它的回文子串在之前一定已经出现过了（如图）。因此加 \(c\) 新增的本质不同的回文子串一定是 \(s[1, n]\) 的最长回文后缀。

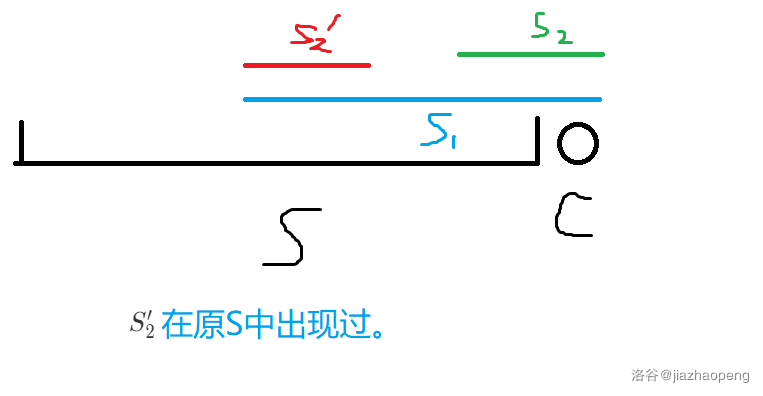
由于每个节点最多只由一个节点转移过来，因此回文树有 \(O(|S|)\) 边。\(fail\) 树上的边显然也是 \(O(|S|)\)。

构造

增量法。

显然，每次我们只需搞出当前串的最长回文后缀即可。由于当前的最长回文后缀一定是先前的一个回文后缀加一个字符，我们可以直接在先前的最长回文后缀上暴跳 \(fail\) 链，直到合法位置（\(s[i - 1 - len[p]] == s[i]\))。显然这是一定合法的，因为 \(fail~tree\) 的根节点长度为 -1，而 \(s[i - 1 - (-1)] == s[i]\) 一定成立。

然后再用类似的方法搞出当前点的 \(fail\) 指针（最长回文后缀).\(len, son\) 随便维护一下即可。

值得注意的是，每添加一个字符，最多只会改 \(fail, len, son\) 数组中的一个位置。

关键代码

下面的代码还顺便求出了 Len[p]，即以 \(p\) 结尾的回文串个数。众所周知，它等于 \(p\) 在 fail tree 上的深度（注意 dep[0] = dep[1] = 0）

int son[N][26], fail[N], lst, len[N], tot;
inline void init() {
	len[1] = -1;
	fail[1] = fail[0] = tot = 1;
}
inline int ins(int pos, int c) {
	int p = lst;
	while (s[pos - 1 - len[p]] != s[pos])	p = fail[p];
	if (son[p][c]) return Len[lst = son[p][c]];
	int np = ++tot, x = fail[p];
	while (s[pos - 1 - len[x]] != s[pos])	x = fail[x];
    x = son[x][c];//注意要向下走一步
	fail[np] = x;
	len[np] = len[p] + 2;
	son[p][c] = np;
	Len[np] = Len[fail[np]] + 1;
	return Len[lst = np];
}

复杂度

分析一下时间复杂度。势能分析瞎搞搞就可以了。 我们死盯一个量：当前的节点在 \(fail~tree\) 上的深度。我们发现，每跳一次 \(fail\) 这个值会减一；每插入一个字符，这个值会加一。这个值始终非负，而最多加了 \(|S|\)。因此时间复杂度是 \(O(|S|)\) 的。

因此，时间 \(O(|S|)\)，空间 \(O(|S|\Sigma)\)。

如果 \(\Sigma\) 比较大，可以使用 \(map\) 存储 \(son\)，时间 \(O(|S|log\Sigma)\)，空间 \(O(|S|)\)。

或者还可以直接用邻接链表存 \(son\)。

显然，每次最多只加一个节点，因此 PAM 的节点数是不超过 \(n\) 的。

拓展 ： 支持前后加字符

题目：hdu 5421 Victor and String

与向后加字符类似，我们可以维护最长回文后缀的指针 \(fail'\)，形成两棵 \(fail~tree\) 。并且我们发现一个神奇的性质：如果一个回文串 \(t\) 的最长回文后缀为 \(t[i...|t|]\)，那么根据回文串的对称性，其最长回文前缀为 \(t[1...|t|-i+1]\)，并且这两个回文串是一样的。也就是说， \(fail\) 指针和 \(fail'\) 指针指向的是同一个节点 ！那么我们就方便很多了，只需要多维护个 \(lst\)，前后插入字符的同时都维护一下 \(fail\) 指针，整棵树的形态就是对的。

唯一一点需要注意的是，我们在前面插入一个字符 \(c\)，最当前串的最长回文后缀可能产生影响，当且仅当插入 \(c\) 后整个串是一个回文串（显然）。因此注意修改后缀的 \(lst\)。后面插入对前缀的影响同理。

科技 ： 回文拆分

将 \(s\) 划分为的 \(k\) 段回文串，最小化 \(k\)。\(|s| \ge 5 \times 10^5\)

显然有个简单的 \(O(|s|^2)\) DP：设 \(f(i)\) 表示前 \(i\) 个字符的答案。当 \(s(j+1...i)\) 为回文串时有如下转移：

\[f(i)\gets f(j)+1 \]

现在我们要通过一个科技来优化这一DP。这个科技oi-wiki上讲得要更详细些。当然也可以参考 lhm_liu的博客

基本结论及证明

oi-wiki上给了一堆关于border的结论和证明，这里简单提及一点。

1. \(t\) 是 \(s\) 的后缀 \(+\) \(t\) ， \(s\) 为回文串 \(\to\) \(t\) 是 \(s\) 的 \(border\)

2. \(t\) 是 \(s\) 的\(border\) \(+\) \(s\) 为回文串 \(\to\) \(t\) 为回文串

3. \(t\) 是 \(s\) 的 \(border\) \(+\) \(t\) 是回文串 \(+\) \((2|t|\ge |s|)\) \(\to\) \(s\) 为回文串。

4. 回文串 \(t\) 是回文串 \(s\) 的最长真回文后缀 \(\to\) \(|s|-|t|\) 为 \(s\) 的最小周期（最小循环节，但是可以有“一半“循环节的情况，如 \(ab\) 为 \(ababa\) 的最小周期）

5. （重点）若 \(y\) 是 \(x\) 的最长真回文后缀， \(z\) 是 \(y\) 的最长真回文后缀，它们的关系为 \(y=v+z,x=u+y=u+v+z\)，如图（来自oi-wiki），那么有:\(|u| \ge |v|\)，且当 \(|u|=|v|\) 时 \(u=v\)，当 \(|u|>|v|\) 时 \(|u| > |z|\)。

   

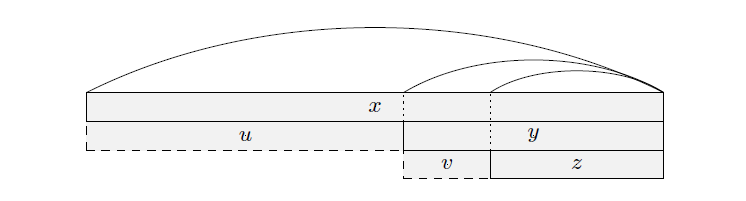
第 5 点的证明可以参考下图。

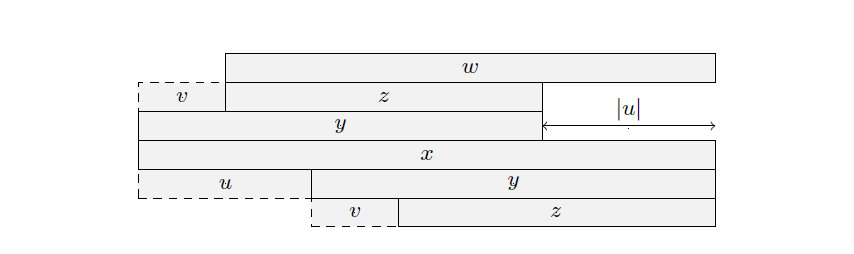
根据引理 4，\(|u|\) 为 \(x\) 的最小周期， \(|v|\) 为 \(y\) 的最小周期，显然 \(|u| \ge |v|\)。既然 \(y\) 为 \(border\)，我们可以把 \(y\) 移到前面，这样看来 \(v\) 一定是 \(u\) 的前缀，于是第一种情况就显然了。

将 \(x\) 删掉 \(v\) 得到 \(w\)，据上图显然 \(z\) 为 \(w\) 前缀，且 \(|w|-|z|=|u|\)，如果 \(|z| \ge |u|\)，那么根据引理 3，\(w\) 为回文串，且比最长回文后缀 \(x\) 要长，矛盾，故不可能 \(|z| \ge |u|\)，于是第二种情况成立。

6. （重要结论）一个回文串的回文后缀的长度集合可以被表示成不超过 \(O(log|s|)\) 个等差数列。（可以由引理 5 直接推出）

算法流程

我们可以在回文树上多维护两个信息：diff[x] 和 slink[x] 分别表示 len[x] - len[fail[x]] 及 x 所在的等差数列的长度最小的那个节点（或者说下一段等差数列的第一个节点）

根据上面那个重要结论，我们在一个回文串节点 x 处暴力跳 slink[x] 的复杂度为 \(O(log|s|)\) 的。

我们可以维护 DP 数组 f[i] 的同时动态维护 g[x]，表示当前 \(1...i\) 的回文后缀中，以 x 作为最长的那个后缀的等差数列的所有DP值的最小值。当新加入一个字符 \(s(i)\) 的时候，g[x] 会多一个 f[i - len[slink[x]] - diff[x]]，具体见图片（仍然来自 oi-wiki）：

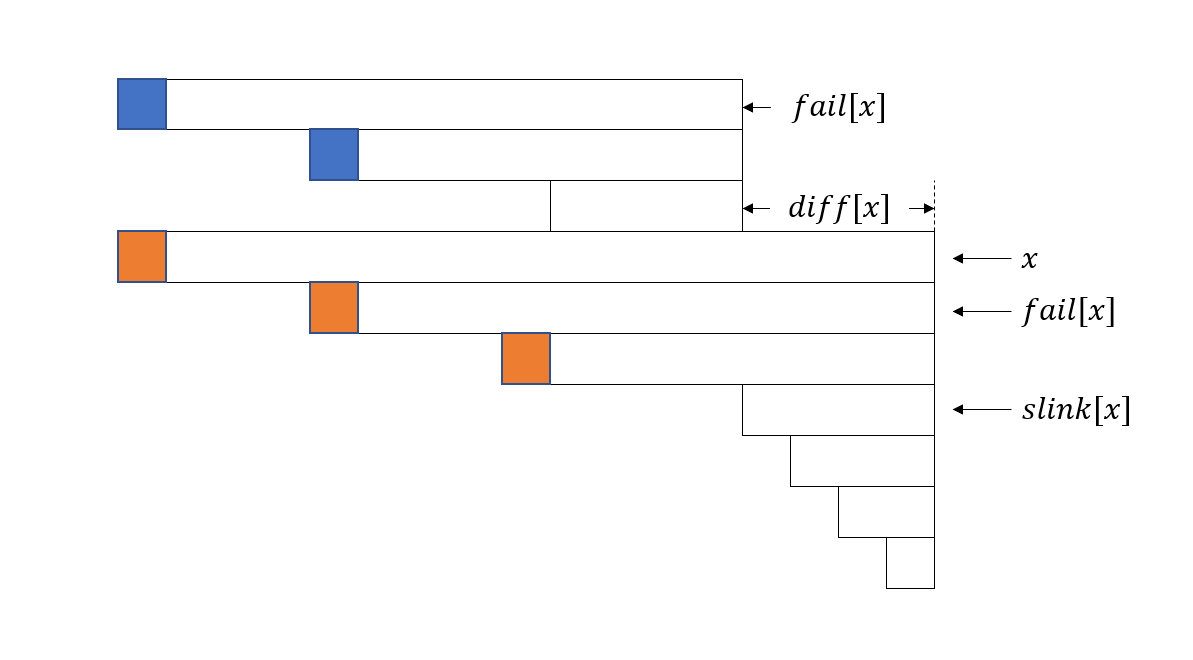
然后在更新 g[x] 的同时更新一下 f[i] 即可。

值得一提的是，那个 \(g(x)\) 永远维护的是 \(x\) 所表示的回文串中最近的那个的信息（不然那次你干啥了？）于是我们可以直接放心大胆地用那些信息，不用担心它们是其它的回文串的信息。

例题

模板题

给个模板吧。ins 函数就多了个 diff 和 slink 的维护，其余不变。注意 work 函数中要特判 if(slink[p] != fail[p])，是因为如果 slink[p]!=fail[p] 的话 g[fail[p]] 记的就是另一组等差数列的答案了，而我们想要干的是把这组等差数列的剩余的f值统计上。

inline void ins(int pos) {
	int p = lst, c = s[pos] - 'a';
	while (s[pos] != s[pos - 1 - len[p]])	p = fail[p];
	if (son[p][c])	return lst = son[p][c], void();
	int np = ++tot; 
	int q = fail[p];
	while (s[pos] != s[pos - 1 - len[q]])	q = fail[q];
	fail[np] = q = son[q][c];//bug2
	son[p][c] = np; len[np] = len[p] + 2;//bug3
	diff[np] = len[np] - len[q]; slink[np] = diff[np] == diff[q] ? slink[q] : q;
	lst = np;
}

inline void work() {
	scanf("%s", s + 1);
	int n = strlen(s + 1);
	f[0] = 0;
	for (int i = 1; i <= n; ++i) {
		ins(i);
		for (int p = lst; p; p = slink[p]) {
			g[p] = f[i - len[slink[p]] - diff[p]] + 1;//bug4
			if (slink[p] != fail[p])	MIN(g[p], g[fail[p]]);
			MIN(f[i], g[p]);
		}
	}
	printf("%d\n", f[n]);
}

CF906E Reverses

（好像这种题都类似的套路）

考虑如果 \(abc \to cba\)，那么我们把它们交叉起来，成为 \(acbbca\)，一定是一个长度为偶数且右端点为偶数位置的回文串。并且 \(a \to a\) 将成为 \(aa\)，是不用花费代价的，否则都需要花费代价。于是直接DP即可。

CF932G Palindrome Partition

方法同上。不过这次是把 \(s\) 和 \(s\) 的反串交叉起来。

题目：

CF17E Palisection

正难则反，考虑互不相交的回文子串对数。我们可以在前面的那个子串的时候统计答案。那么贡献就是以某个点为右端点的回文子串个数 × 以某个点为左端点的回文子串个数的后缀和。正反两遍 PAM 求解即可。注意这题卡空间，需要用 map 或者邻接链表存 \(son\)。

双倍回文

求最长 \(AA^rAA^r\) 串长度。

一定存在一个右端点，使得其最长回文后缀为最长的 \(AA^rAA^r\)。否则假设其为 \(AB\)，其中 \(B\) 为最长合法的 \(AA^rAA^r\)，那么由于其为回文后缀，一定也可以表示为 \(BA^r\)，\(B\) 会在前面考虑到。

现在我们只需要判断最长回文后缀是否合法。要求：

• 长度为 \(4\) 的倍数

• 存在一个回文后缀，其长度恰好为其一半

可以维护 fail 的同时再维护个 halfail，表示最长的长度不超过 len[cur] 的回文后缀。