P5494 【模板】线段树分裂 题解

很久之前写的题目了，写一篇题解来回忆一下。

线段树合并与分裂#

线段树是一个非常有意思的数据结构，它支持很多的操作，包括分裂与合并。

合并#

例题：P4556 [Vani有约会]雨天的尾巴 /【模板】线段树合并

首先，支持合并的操作的线段树，出于空间与时间的考虑，需要写动态开点线段树。

考虑如何合并两颗线段树。

首先会遍历到第一个节点，发现两棵线段树都有，那么就将维护的东西合并。

然后到第二个节点，同理，接着，发现第一棵线段树没有 $(1,2)$ 号节点，那么直接接上，无需遍历。

然后合并 $(3,3)$，接上 $(4,5)$，这就是大概的算法流程。

总结一下。

1. 遍历到一个节点，若有一方没有，则直接接上。

2. 否则，继续遍历，合并信息。

3. 当然，合并完后没有用的节点需要删除。

inline int merge(int p1 , int p2 , int l , int r)
{
    if(!p1 || !p2) return p1 + p2;
    t[p1].val += t[p2].val;
    if(l == r) { del(p2); return p1; }
    t[p1].l = merge(t[p1].l , t[p2].l , l , (l + r) / 2);
    t[p1].r = merge(t[p1].r , t[p2].r , (l + r) / 2 + 1 , r);
    del(p2); return p1;
}

分裂#

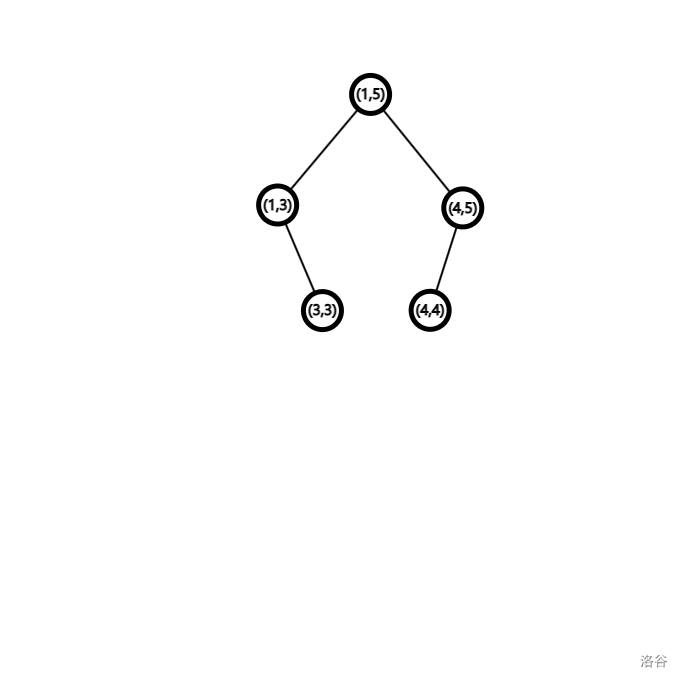
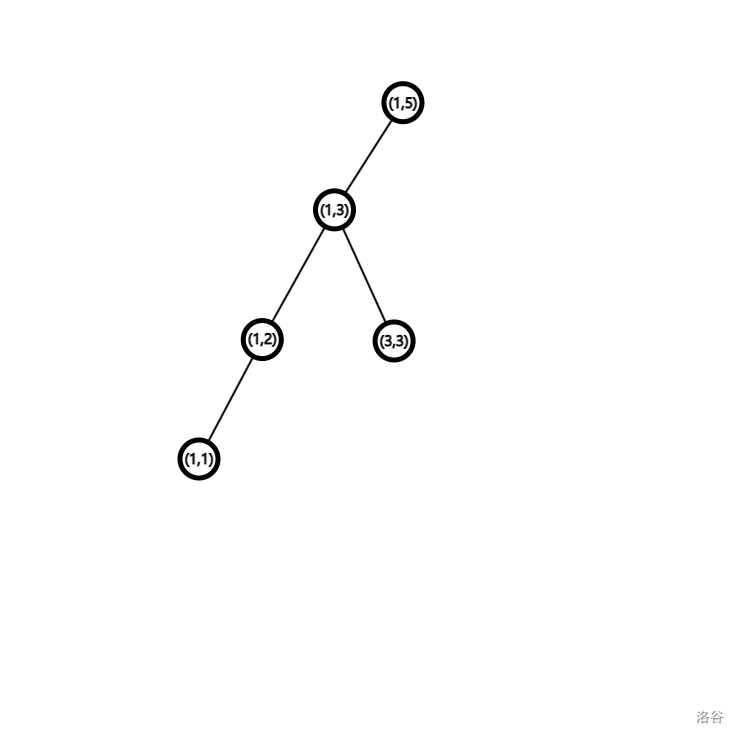
例题：P5494 【模板】线段树分裂

一般来讲，线段树的分裂是将前 $\text{k}$ 个节点分到一颗线段树上，其余的分裂到另一棵线段树上。

我们可以考虑一个和 $\text{FHQ treap}$ 相似的过程。

1. 若此时被分裂的线段树的左儿子子树大小大于等于 $\text{k}$，那么就可以将整个右儿子送给第二棵线段树。

2. 若左儿子子树大小还大于 $\text{k}$ 那么就要到左儿子处继续分裂。

3. 若左儿子子树大小小于 $\text{k}$ 那么就要到右儿子处继续分裂。

inline void split(int x , int &y , int k)
{
	if(!x) return; y = new_node(); int val = t[t[x].son[0]].sum;
	if(val < k) split(t[x].son[1] , t[y].son[1] , k - val);
	else swap(t[x].son[1] , t[y].son[1]);
	if(val > k) split(t[x].son[0] , t[y].son[0] , k);
	t[y].sum = t[x].sum - k , t[x].sum = k;
}

时间复杂度#

合并#

我知道的，大概有两种证明方法。

第一种是我们知道所有的节点一共有 $n\log n$ 个。

而我们每次合并都只会合并两方都有的节点，并且删掉其中之一。

故最多只会删除 $n\log n$ 次，复杂度为 $O(n\log n)$。

第二种可能只是第一种的另一个说法。

我们发现每一次合并都会有叶子节点，一句废话。

可以发现每次会需要 $O(\log n)$。

而只有 $n$ 个叶子节点，故复杂度为 $O(n\log n)$。

仔细想一想，两种都是一个原理。

分裂#

分裂的复杂度就比较好证了。

可以发现，每一次分裂的操作与查询的操作很像。

可以说与查找第 $k$ 个数简直一模一样。

故时间复杂度 $O(n\log n)$

关于此题#

总体来说，线段树的合并与分裂只要掌握思路代码实现比较简单。

最后附上此题代码。

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 200010;

int n, m, cnt, top, tot, stk[N * 32], root[N];

struct Tree
{
    int sum, son[2];
} t[N * 32];

inline int read()
{
    int asd = 0, qwe = 1; char zxc;
    while (!isdigit(zxc = getchar())) if (zxc == '-') qwe = -1;
    while (isdigit(zxc)) asd = asd * 10 + zxc - '0', zxc = getchar();
    return asd * qwe;
}

inline void del(int x)
{
    if (!x)
        return;
    t[x].sum = t[x].son[0] = t[x].son[1] = 0;
    stk[++top] = x;
}

inline int new_node()
{
    return (top ? stk[top--] : ++cnt);
}

inline void update(int &p, int l, int r, int k, int val)
{
    if (!p)
        p = new_node();
    t[p].sum += val;
    if (l == r)
        return;
    int mid = (l + r) / 2;
    if (mid >= k)
        update(t[p].son[0], l, mid, k, val);
    else
        update(t[p].son[1], mid + 1, r, k, val);
}

inline int merge(int x, int y)
{
    if (!x || !y)
        return x + y;
    t[x].sum += t[y].sum;
    t[x].son[0] = merge(t[x].son[0], t[y].son[0]);
    t[x].son[1] = merge(t[x].son[1], t[y].son[1]);
    del(y);
    return x;
}

inline void split(int x, int &y, int k)
{
    if (!x)
        return;
    y = new_node();
    int val = t[t[x].son[0]].sum;
    if (val < k)
        split(t[x].son[1], t[y].son[1], k - val);
    else
        swap(t[x].son[1], t[y].son[1]);
    if (val > k)
        split(t[x].son[0], t[y].son[0], k);
    t[y].sum = t[x].sum - k, t[x].sum = k;
}

inline int ask1(int p, int l, int r, int ql, int qr)
{
    if (!p || l > qr || r < ql)
        return 0;
    if (ql <= l && r <= qr)
        return t[p].sum;
    int mid = (l + r) / 2;
    return ask1(t[p].son[0], l, mid, ql, qr) + ask1(t[p].son[1], mid + 1, r, ql, qr);
}

inline int ask2(int p, int l, int r, int k)
{
    if (l == r)
        return l;
    if (t[t[p].son[0]].sum >= k)
        return ask2(t[p].son[0], l, (l + r) / 2, k);
    else
        return ask2(t[p].son[1], (l + r) / 2 + 1, r, k - t[t[p].son[0]].sum);
}

signed main()
{
    n = read(), m = read(), tot = 1;
    for (int i = 1; i <= n; i++)
    {
        int x = read();
        if (x)
            update(root[1], 1, n, i, x);
    }
    for (int i = 1; i <= m; i++)
    {
        int opt = read();
        if (opt == 0)
        {
            ++tot;
            int p = read(), x = read(), y = read(), tmp = 0;
            int k1 = ask1(root[p], 1, n, 1, y);
            int k2 = ask1(root[p], 1, n, x, y);
            split(root[p], root[tot], k1 - k2);
            split(root[tot], tmp, k2);
            root[p] = merge(root[p], tmp);
        }
        if (opt == 1)
        {
            int x = read(), y = read();
            root[x] = merge(root[x], root[y]);
        }
        if (opt == 2)
        {
            int p = read(), x = read(), q = read();
            update(root[p], 1, n, q, x);
        }
        if (opt == 3)
        {
            int p = read(), x = read(), y = read();
            printf("%lld\n", ask1(root[p], 1, n, x, y));
        }
        if (opt == 4)
        {
            int p = read(), k = read();
            if (t[root[p]].sum < k)
                puts("-1");
            else
                printf("%lld\n", ask2(root[p], 1, n, k));
        }
    }
    return 0;
}