线性插值法
线性插值法
线性插值法(linear interpolation)
转载原地址:https://wiki.mbalib.com/wiki/%E7%BA%BF%E6%80%A7%E6%8F%92%E5%80%BC%E6%B3%95
线性插值法(linear interpolation)
线性插值法是指使用连接两个已知量的直线来确定在这两个已知量之间的一个未知量的值的方法。
如何进行线性插值
假设我们已知坐标(x0,y0)与(x1,y1),要得到[x0,x1]区间内某一位置x在直线上的值。根据图中所示,我们得到两点式直线方程:
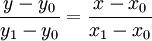
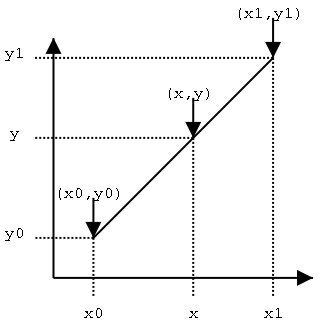
假设方程两边的值为α,那么这个值就是插值系数—从x0到x的距离与从x0到x1距离的比值。由于x值已知,所以可以从公式得到α的值
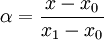
同样,
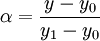
这样,在代数上就可以表示成为:
y = (1 − α)y0 + αy1
或者,
y = y0 + α(y1 − y0)
这样通过α就可以直接得到 y。实际上,即使x不在x0到x1之间并且α也不是介于0到1之间,这个公式也是成立的。在这种情况下,这种方法叫作线性外插—参见 外插值。
已知y求x的过程与以上过程相同,只是x与y要进行交换。
线性插值近似法
线性插值经常用于已知函数f在两点的值要近似获得其它点数值的方法,这种近似方法的误线定义为
RT = f(x) − ρ(x)
其中ρ表示上面定义的线性插值多项式
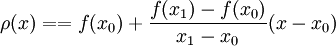
根据罗尔定理,我们可以证明:如果f有两个连续导数,那么误差范围是
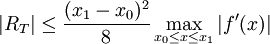
正如所看到的,函数上两点之间的近似随着所近似的函数的二阶导数的增大而逐渐变差。从直观上来看也是这样:函数的曲率越大,简单线性插值近似的误差也越大。
线性插值法是认为现象的变化发展是线性的、均匀的,所以可利用两点式的直线方程式进行线性插值。
两点式的直线方程式为:
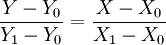 即
即 
式中 X0,Y0,X1,Y1——已知的统计数据;
X——X0,X1之间的任何数据;
Y——与X对应的插值数据。
例 某地区居民货币收入和消费支出情况如表1所示。试推算该地区居民收入为19.5亿元时,其相应的消费支出是多少?
表1 居民货币收入和消费支出资料(单位:亿元)
| 顺序 | 货币收入(x) | 消费支出(y) |
| 0 | 18.2 | 15.8 |
| 1 | 19.8 | 17.2 |
解 
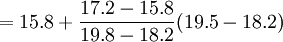
= 16.9
所以,当该地区居民收入是19.5亿元时,其消费支出是16.9亿元。
由于线性插值法只利用两点的对应值宋推算两点之间的对应值,而两点对应值本身往往受到各种偶然因素的影响,所以线性插值结果可能误差较大。
说了那么多,我真正用到的就是用了一个公式
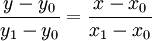


 浙公网安备 33010602011771号
浙公网安备 33010602011771号